Focus on
大学レベルの物理・数学・化学
大学受験レベルの数学・物理・化学
公務員試験 判断推理・数的推理
テキスト一覧
量子力学1.量子力学と確率解釈
1.1 量子力学はなぜ生まれたか 1.2 古典力学の限界を示す実験の一例【ダブルスリットと電子銃】
1.3 質点と量子との対比・とりうる確率について 1.4 複素ベクトルの内積・エルミート演算子・固有値と固有ベクトル
1.5 内積や演算子の考え方を量子の記述に用いる 1.6 量子を状態ベクトルで表すとは?
1.7 オブザーバブル【量子力学での物理量とは】 1.8 固有ベクトル同士の関係【序章】
1.9 状態を時間発展させシュレーディンガ方程式を導く
2.ハイゼンベルグの不確定性原理と位置・運動量
2.1 ハイゼンベルグの不確定性原理 2.2 同時固有状態と縮退について
2.3 ユニタリー演算子と平行移動演算子 2.4 連続的にパラメトライズされた固有ベクトル
2.5 運動量演算子を位置の固有ベクトルに作用させる
3.調和振動子とコヒーレント状態
3.1 量子力学の調和振動子問題を解こう 3.2 調和振動子のエネルギー演算子と自然数演算子
3.3 上昇演算子・下降演算子・自然数演算子の性質 3.4 調和振動子のエネルギー離散性と最低エネルギーについて
3.5 調和振動子のコヒーレント状態
古典力学
0.古典力学のプロローグ
●力学って、なんだ? ●作用・反作用の法則とは?
●運動の法則!よく知られるF=maの式について。
●プロローグの最後に、慣性の法則について。
1.速度と加速度の定義
1.1 速度と加速度 1.2 文字式を使って表してみよう
1.3 マイナスの速度と加速度
2.運動方程式と簡単な運動
2.1 実際に運動を式で記述してみよう 2.2 力のかからない運動
2.3 力がつりあっている運動その1 2.4 力がつりあっている運動その2
2.5 加速度が一定の運動
3.いろいろな力の大きさ
3.1 いろいろな力の種類を知ろう! 3.2 まずは万有引力
3.3 重力とは! 3.4 垂直抗力について 3.5 張力について
3.6 静止摩擦力と動摩擦力 3.7 ばねによる力
3.8 浮力とは
4.一様重力下での物体の運動
4.1 重力下での物体の運動 4.2 自由落下
4.3 鉛直投げ上げ 4.4 鉛直投げ下げ 4.5 斜方投球
4.6 水平投球
5.運動量保存則
5.1 運動方程式を積分しよう(運動量保存則) 5.2 運動量と力積について
5.3 運動量保存則を導こう 5.4 運動量保存の法則をさらに一般化する
5.5 跳ね返り係数とは 5.6 運動量保存の法則を適用できる例題をいくつか
6.エネルギー保存則
6.1 運動方程式を積分しようその2!【エネルギー保存の法則】 6.2 3次元座標系でのエネルギー保存則
6.3 保存力による仕事 6.4 重力による位置エネルギー
6.5 ばねの力による位置エネルギー
7.角運動量保存則
7.1 運動方程式を積分しようその3!【角運動量保存則】
7.2 角運動量保存の法則を導こう
8.ばね振動運動
8.1 調和振動について 8.2 空気抵抗がある場合のばね運動について
8.3 外部強制力のある振動について 8.4 共振現象について
8.5 2連振動について
9.中心力場の運動【万有引力】
9.1 重心と相対座標 9.2 運動の極座標表示
9.3 運動方程式を解釈しよう(θ方向) 9.4 運動方程式を解釈しよう(r方向)
9.5 極座標表示を用いたエネルギー保存則 9.6 ケプラーの法則
9.7 等速円運動 9.8 鉛直打ち上げ運動
10.ガリレイ変換と散乱問題
10.1 ガリレイ変換と相対性原理 10.2 重心座標系と実験室座標系
10.3 完全弾性衝突 10.4 静止している玉への衝突
10.5 ラザフォード散乱 10.6 散乱断面積
11.慣性力
11.1 慣性力とは 11.2 等加速度直線運動する座標での慣性力について
11.3 平面的に運動をする座標系での慣性力 11.4 遠心力について
11.5 コリオリ力について 11.6 3次元回転座標系での慣性力
11.7 地球に表面における慣性力 11.8 フーコーの振り子
12.解析力学とラグランジアン
12.1 力学を再構築しなおそう 12.2 3次元でのラグランジュ方程式
12.3 慣性の法則とガリレイの相対性原理について 12.4 多粒子系への拡張
12.5 ラグランジアンの不定性について 12.6 ラグランジアンと運動の相似について
12.7 ラグランジアンと空間や時間の一様性、等方性について
13.ラグランジアンの応用
13.1 極座標でのラグランジアン 13.2 拘束運動にラグランジュ方程式をなぜ適用できるか?
13.3 2連平面振り子の運動 13.4 ラグランジアンを用いて複雑な束縛問題を解こう①
13.5 ラグランジアンを用いて複雑な束縛問題を解こう②
14.ハミルトニアンの導入
14.1 ハミルトニアンを生成する 14.2 ハミルトニアンの性質(時間に陽、摂動)
14.3 ポワソン括弧式の導入 14.4 ポワソン括弧式と保存量
14.5 終点の関数としての作用とハミルトン-ヤコビの方程式
Sample
3.5 調和振動子のコヒーレント状態
一般にレーザー光のように、波形が時間的に変化しない場合、コヒーレンスが強いという。量子力学で状態は、所定の固有状態で展開され、その係数は確率振幅を意味する。係数すなわち確率振幅の波形が時間とともに変化しない場合、量子状態としてコヒーレンスが強いという。
調和振動子の場合は、下降演算子の固有ベクトルそれ自身が、コヒーレント状態であるため、考えやすい。

では、順を追って|λ>がどのような状態かを検証していこう。
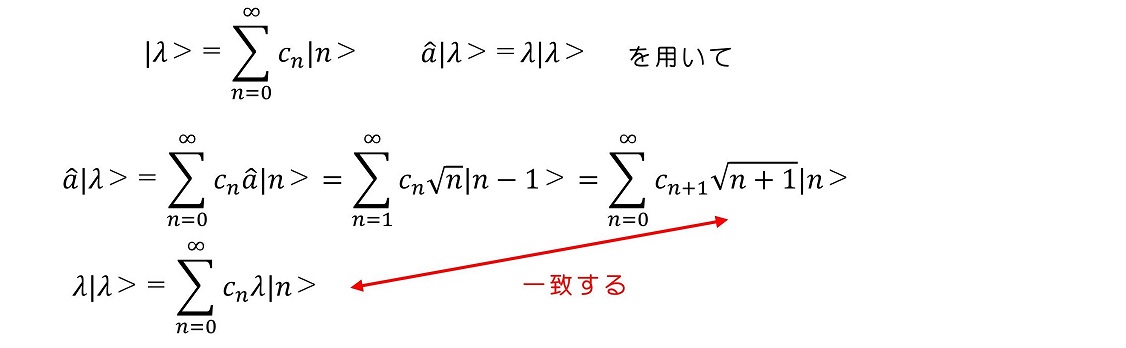
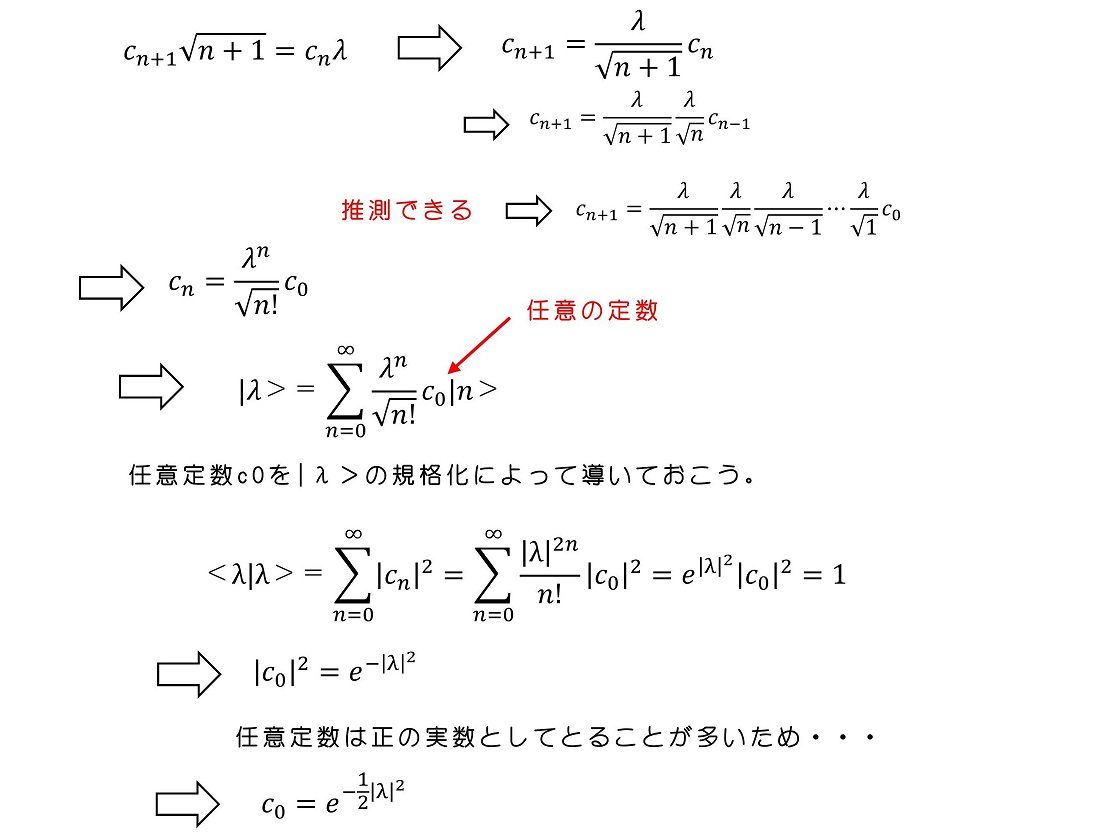
(i)|λ>を|n>を用いて表そう
十分に議論されている|n>を用いてコヒーレント状態を展開してみよう。
(ii)|λ>を|0>を用いて表そう
一方、|n>は|0>を用いて表すこともできる。
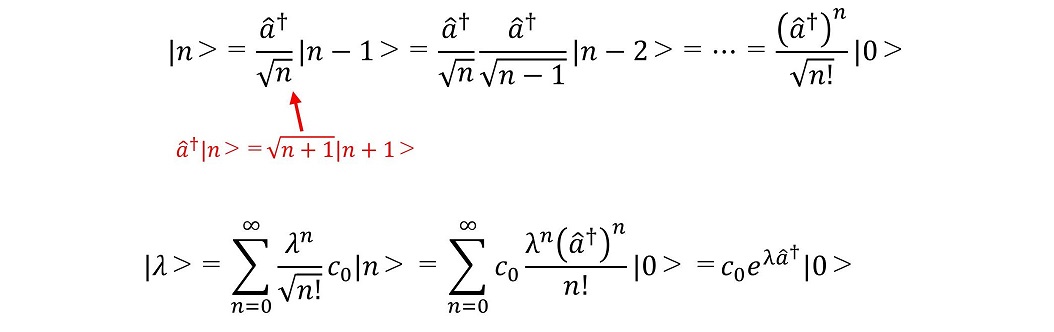
(iii)|λ>を|x>で展開しなおそう
コヒーレントか否かは、位置の固有状態で展開した係数が時間とともにどのように変化するかで決定される。まずはt0での係数を求めよう。


(iv)|0>を|x>で展開する
ψ0(x)=<x|0>だけは、簡単な微分方程式を解くことで解を導きだすことができる。

(v)<x|λ>を関数のみで記述する

コヒーレント状態の確率分布を導くことができた。さて、λは下降演算子の固有値であり、下降演算子はエルミートではないため、一般に複素数である。確率分布をもう少しわかりやすくするために、λの実部と虚部を明らかにして書き直そう。
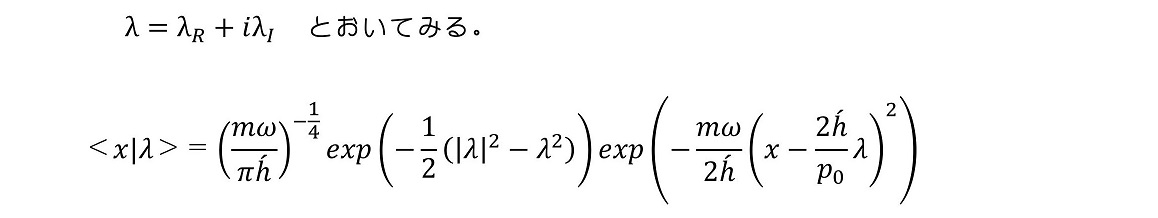

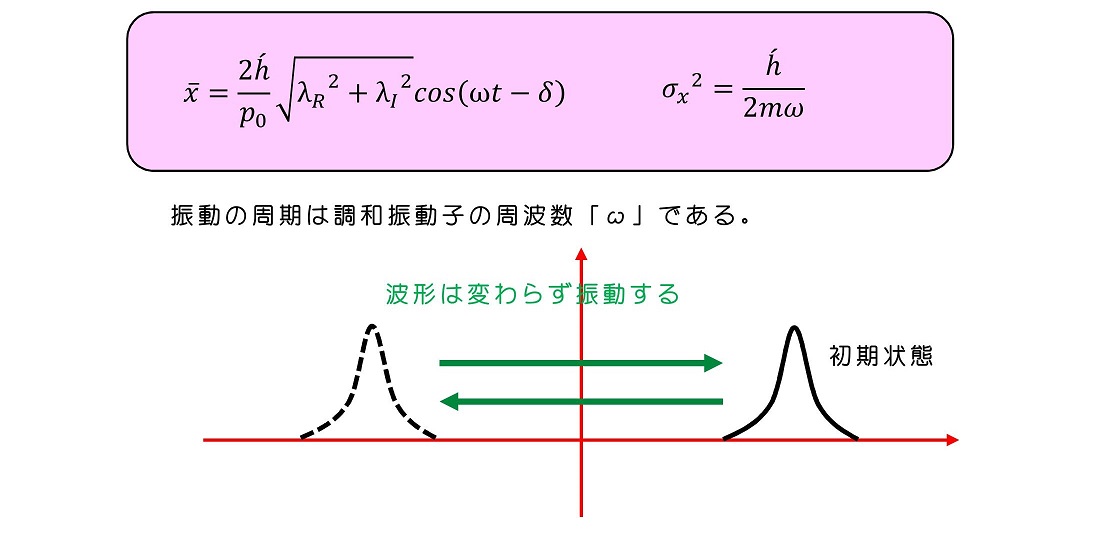
(vi)コヒーレント状態の時間発展を調べよう
確かにコヒーレント状態であることを、時間発展を調べることで調査しよう。時間発展の演算子を作用させればよい。
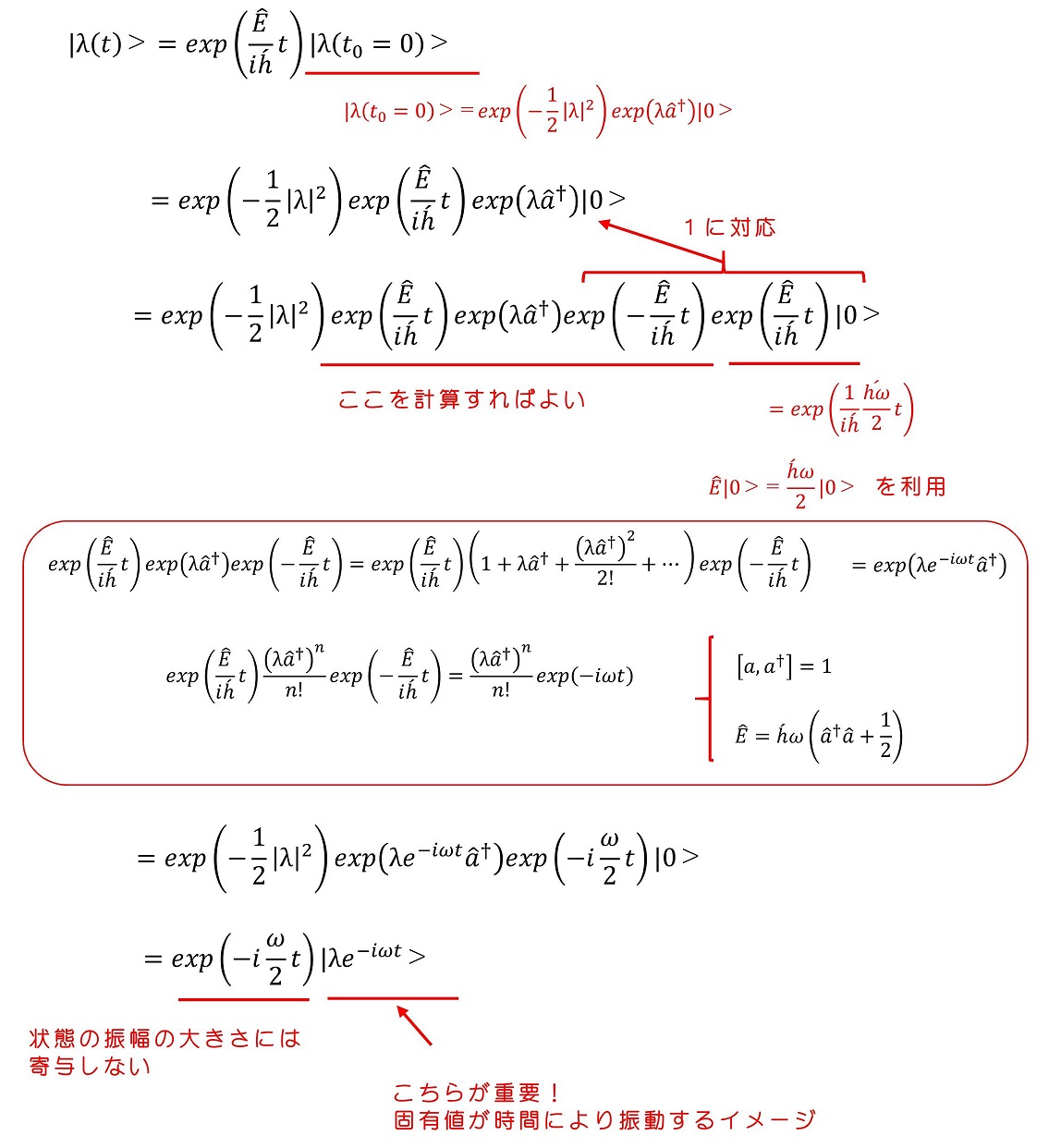
初期時刻でコヒーレント状態がλという複素数で表されたのに対し、t秒経過後ではλexp(-iωt)という複素数で状態が特徴づけられるようになっている。さて、この複素数の実部と虚部を求めてみよう。
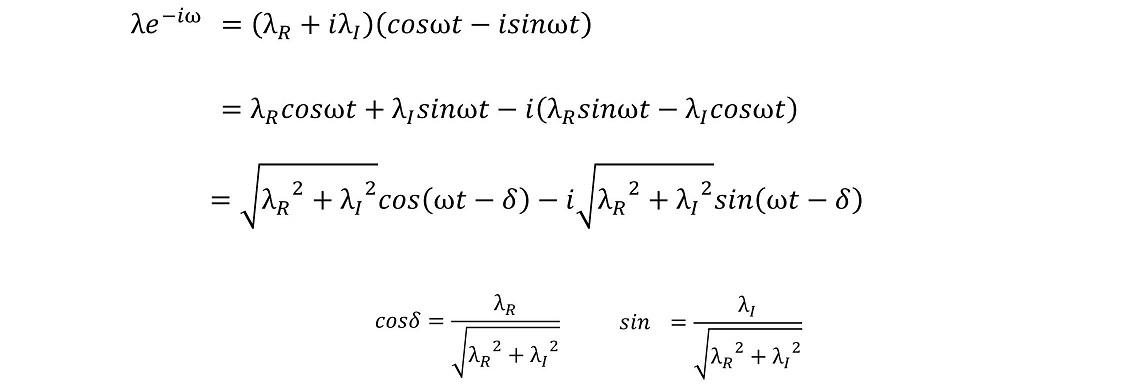
この計算結果を用いて、任意の時刻での位置の平均と分散を計算することができる。