2.1 実際に運動を式で記述してみよう!
速度と加速度の定義ができたので、ここから本格的に『力学』らしいことが始まるよ。物体に力が加わったとき、運動を始めるわけだね。このときプロローグで紹介した運動の3つの法則に従って、力がかかったり、運動したりするよ。
(1)力のかからない運動
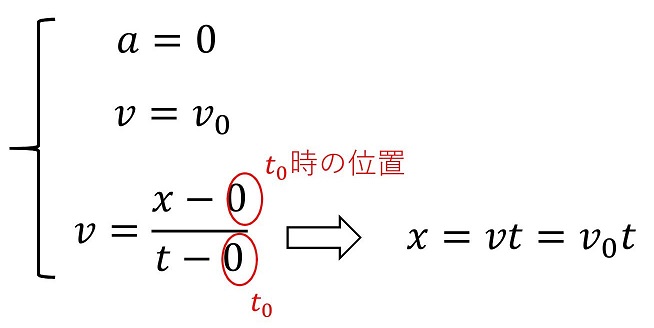
最も簡単な運動は、力のかからない運動だね。運動の3つの法則のうち、①は力が生じたときの法則だから、今回は考えなくてよいよ。
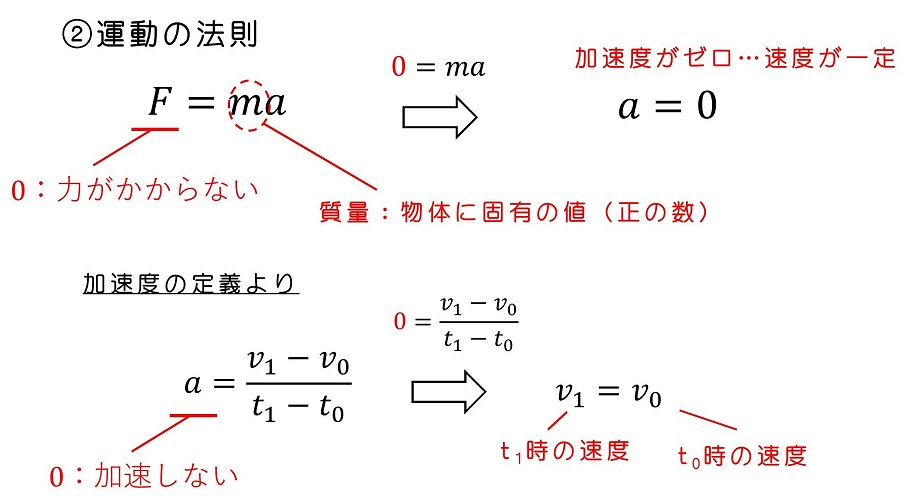
もし、t0時の速度v0が6m/sなら任意の時刻t1の速度も同じ6msだし、もし速度v0が0m/s(停止している)なら、任意の時刻t1の速度も0m/sだ。よく見ると、これは③の慣性の法則を表しているね。②運動の法則は、③慣性の法則も包括的に表していたんだよ。
力がかからないため、②運動の法則を用いると、加速度=0がわかる。

次に、加速度の定義を用いる。
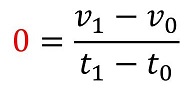
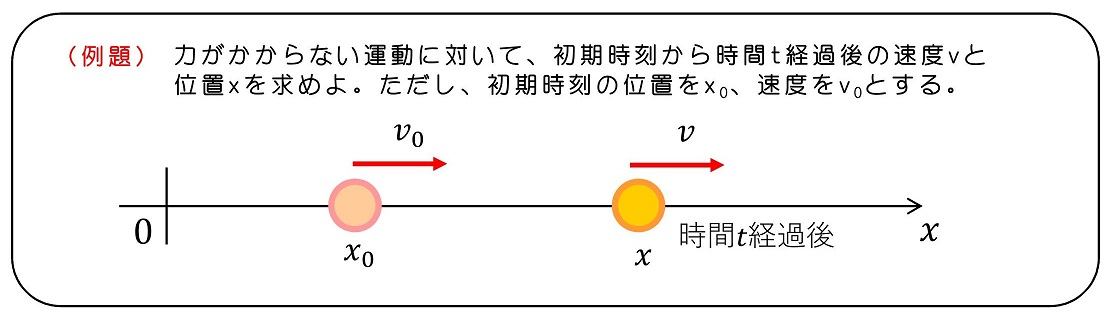
初期時刻からの経過時間tとは、言い換えると初期の時刻にストップウォッチを押して、ストップウォッチの表示時間をtとおくということだ。すなわち、t0=0としてt1=tとすればよいね。またこの時、v1=vだ。
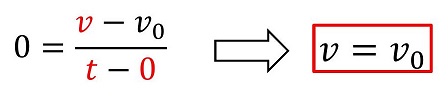
次に、速度の定義を用いる。
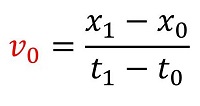
再びt0=0としてt1=tとすれ。またこの時、x1=xとなる。

図にすると、わかりやすいね。
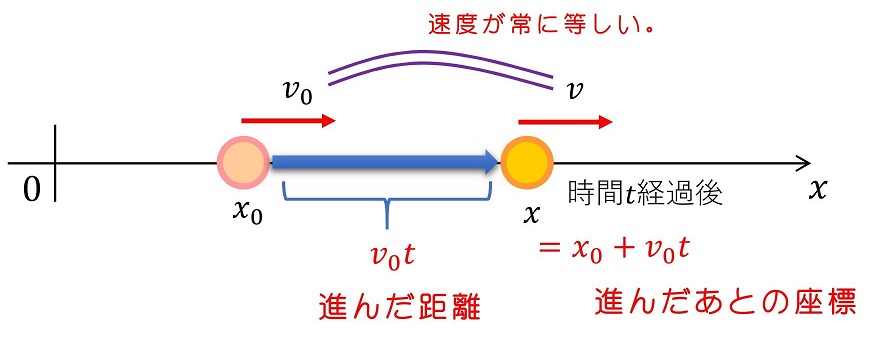
(2)力が釣り合っている運動(状態)その1
次に、力が釣り合っている状態を考えてみよう。さて、力が釣り合っているとはどういうことだろう?机の上に置いてある玉を考えてみようか。玉や机は動かないだろうね。ではこれらにはどんな力が働くだろう?
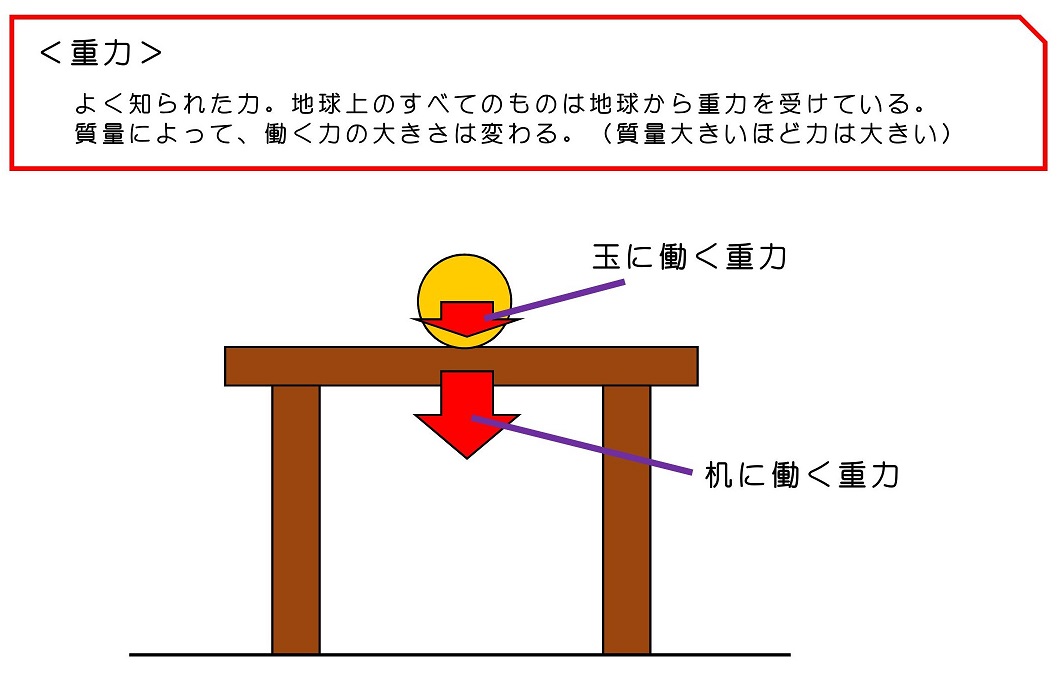
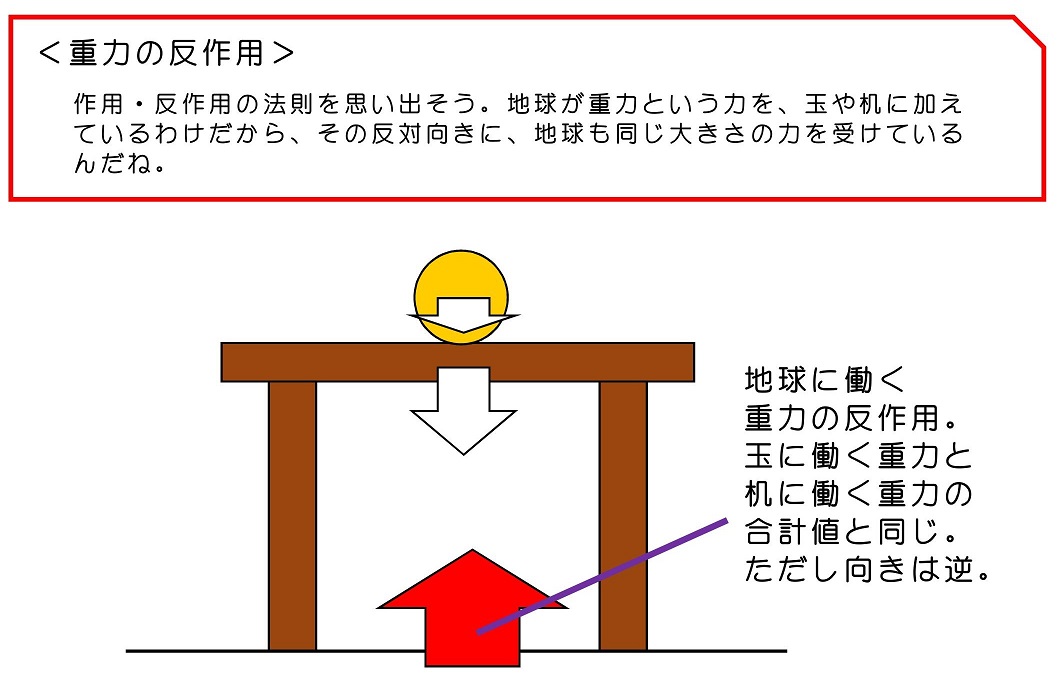
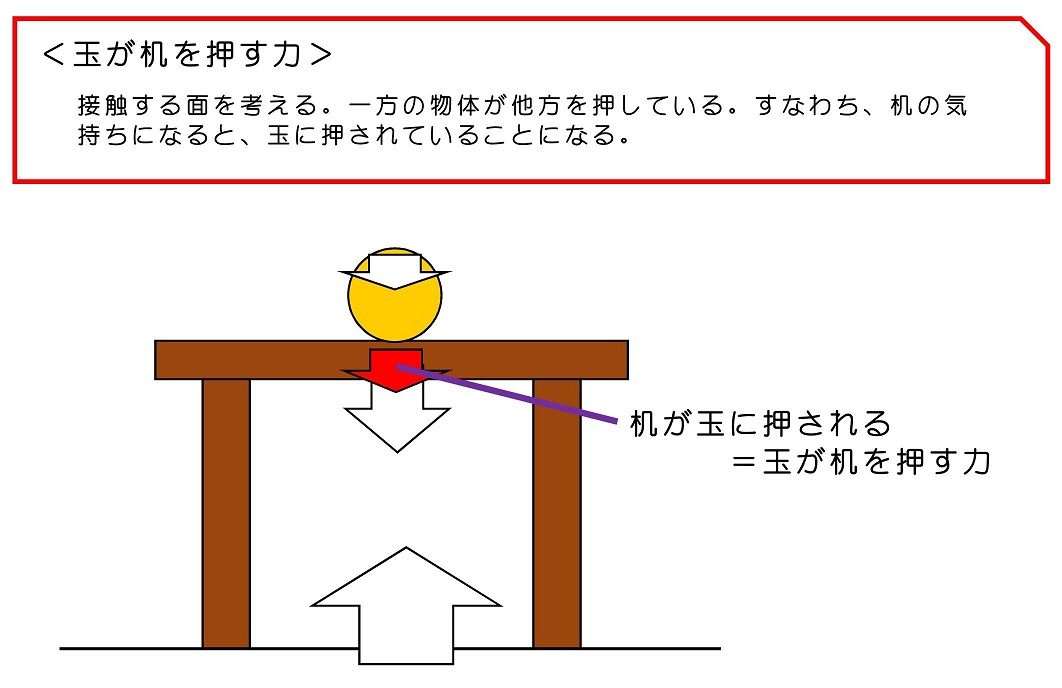
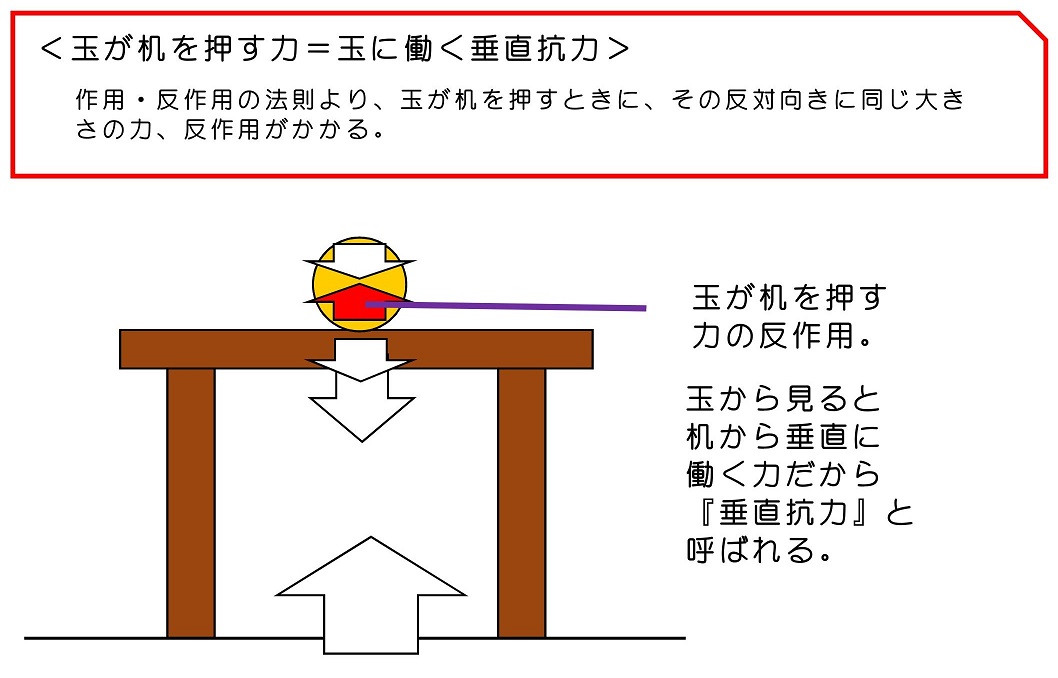
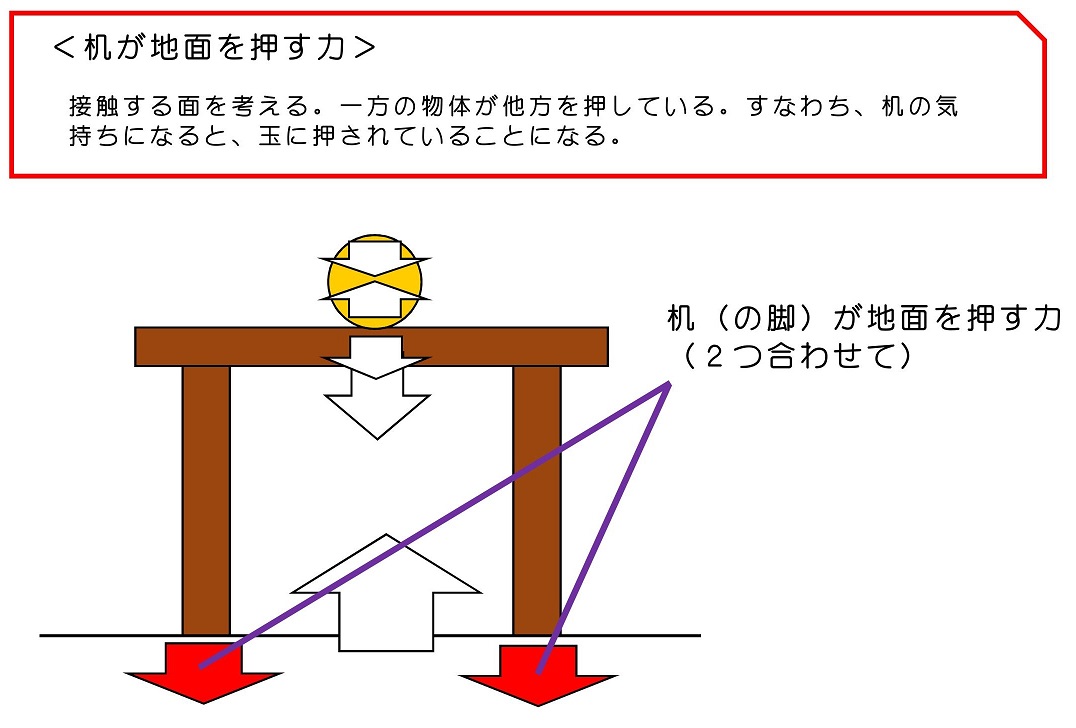
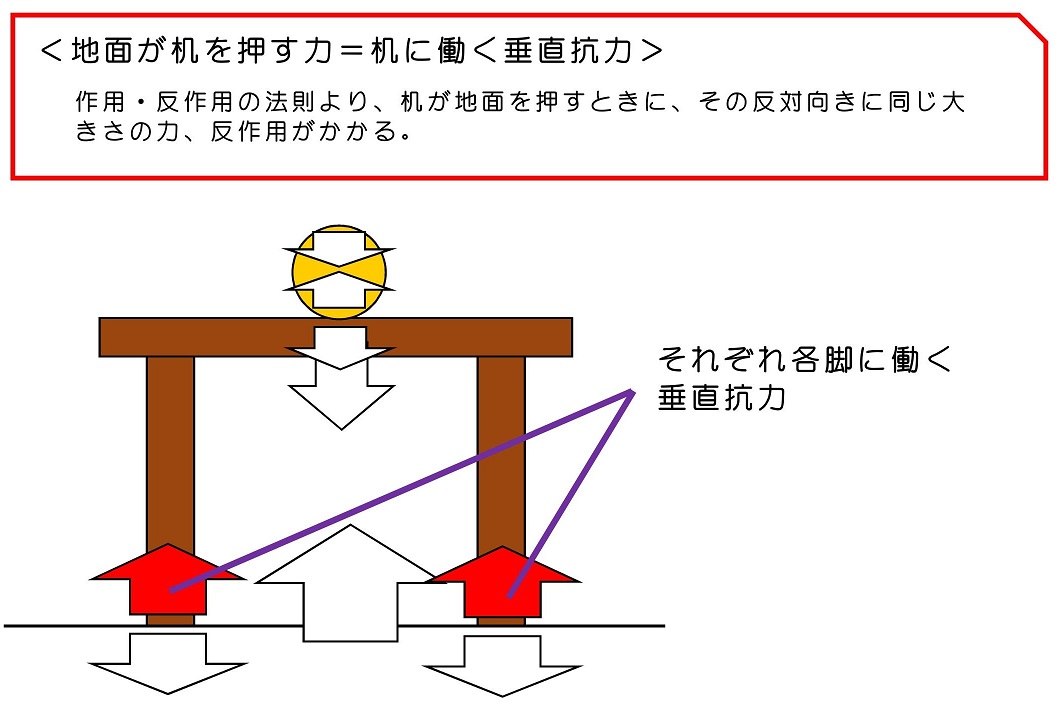
少し複雑だったかな?玉と机、たった2個の物体だったとしても、これだけたくさんの力が働くことになるんだね。見渡すと、世の中の構造はもっと複雑な状態になっているはずだよね。例えば、普段何気なく見る高層マンションおよびその内部に置かれた家具などには、これとは比べ物にならない複雑な力が働きながらそこに建っているんだよ。
②運動の法則を用いて検証すると…
力が働いているわけだから、②運動の法則に従って、運動するはずだよね。F=maの方程式をたてるわけだ。今は玉の運動、机の運動それぞれを知りたいから、玉、机、それぞれに対してF=maの運動方程式をたてよう。

力が軸と同じ向きを向いているか、向いていないかと、加速度が軸と同じ向きか否かは、同じことを意味しているんだったね。運動を調べるとはすなわち、物体がどのような速度で動いていくかを検証すること、だから、加速度の正負をしっかり調べることは非常に重要だよ。まずは座標軸をとって、軸と同じ向きの力を正、逆向きを負と定義するところから始めよう!
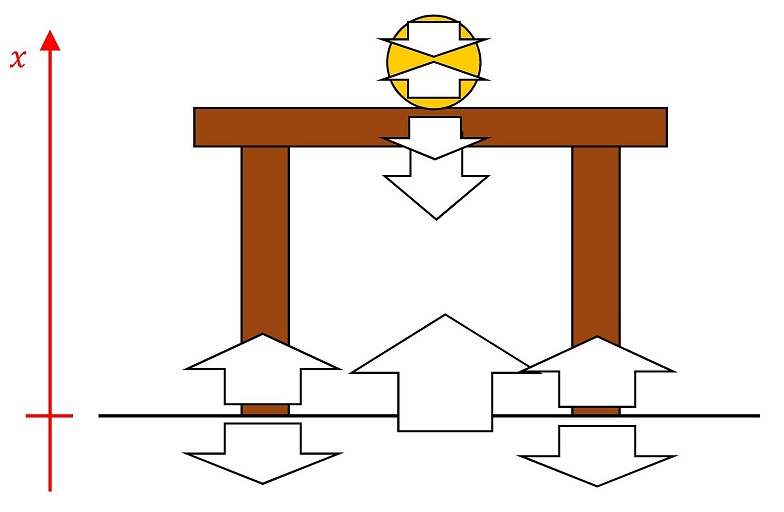
今回、力は上下にしか働いていないから、運動するとしたら上下だよね。だから座標も上下の1次元にとるよ。軸の矢印の向き(上向きか下向きか)や原点の位置(今の図では地面の位置だが)をどこにとるかは好きにしてよいよ。自分で設定した軸に従って方程式をたてればよいだけだからね。重要なのは、『軸をどう設定するか』よりも、『軸に従ってどう運動を記述するか』のほうだからね。
玉に働く力と方程式
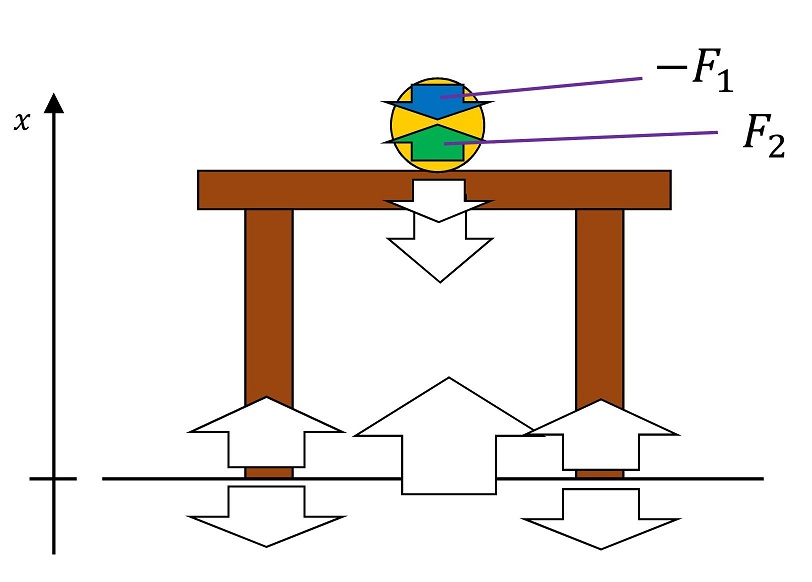
玉に働く力は2つだけだ。それぞれx軸と向きが同じか逆かで正負を定めているよ。(-F1とF2)運動方程式をたててみよう。玉の質量はmとおくよ。
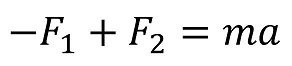
式についての詳細な解析は後にして、次に机に働く力と運動方程式を作ろうか。
机に働く力と方程式
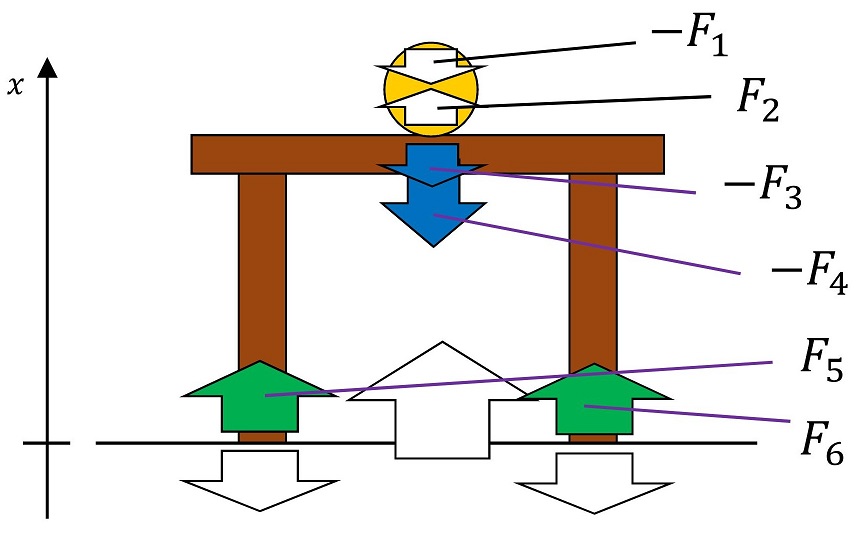
机に働く力は4つになるね。正負含めて文字でおいているよ。さあ、運動方程式をたてよう。机の質量をMとおこう。玉の加速度と区別するために、机の加速度はa'としようか。
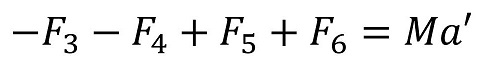
力の大きさを整理しよう
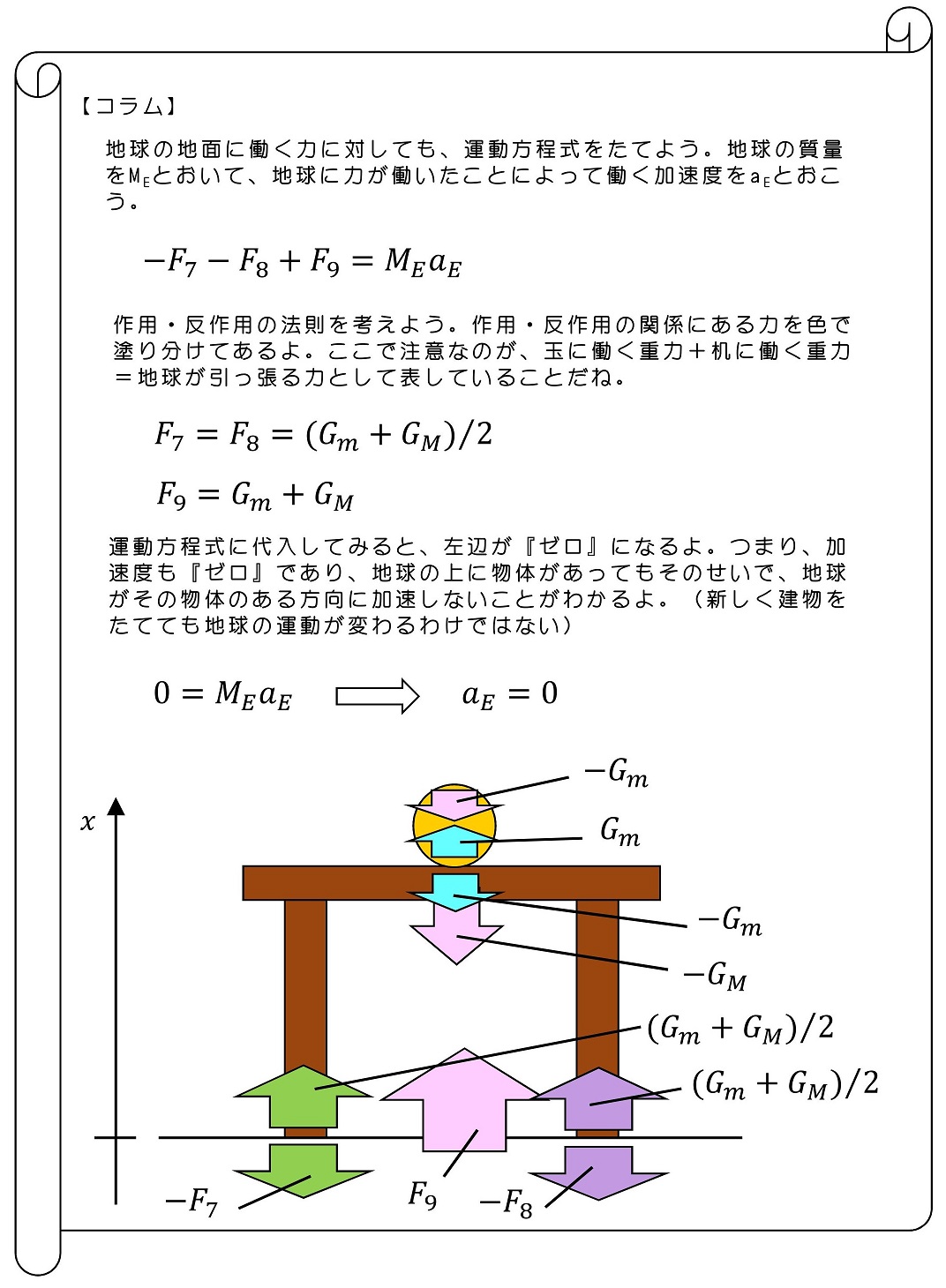
今、6この力に対してF1からF6を割り当てたわけだけど作用・反作用の法則に基づき、向きは確かに逆だけど、大きさが等しくなる力があるね。さらに、重力という力の大きさは、その物体の質量によって一意に決まることが知られているよ。(別の章で詳しく説明するよ)よって、玉、机それぞれに働く重力の大きさをGm、GMとおきなおそうか。
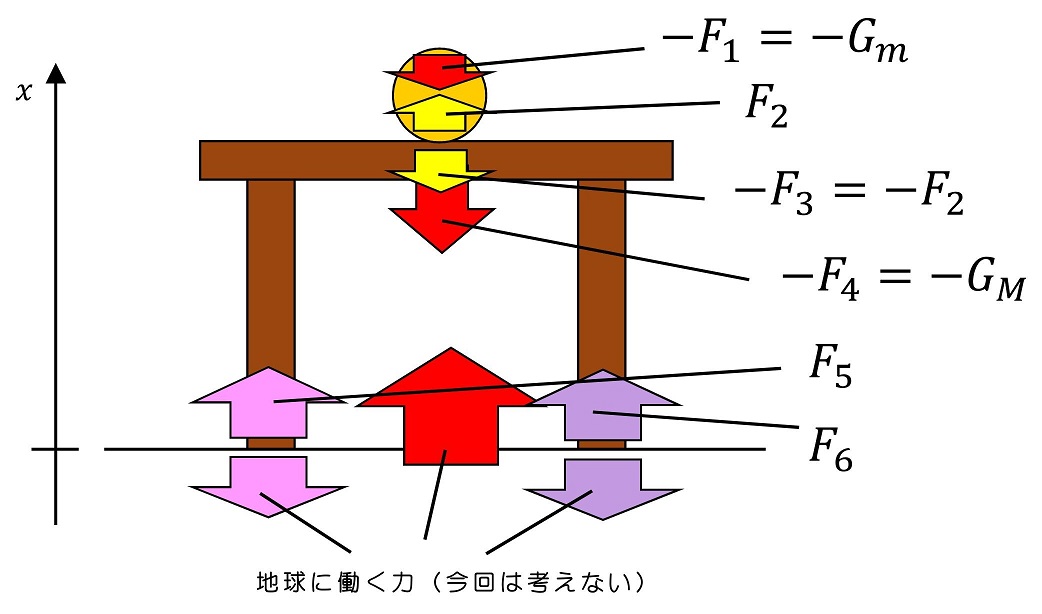
作用・反作用の組み合わせごとに色を塗り分けだよ。ここで注意すべきは、玉に働く重力と机に働く重力の反作用として、両方の反作用足し合わせとしてF6を考えていることだったね。ちなみに、今回は地球の運動は考えていないから、地球に働く3つの力を以下では考えないこととするよ。
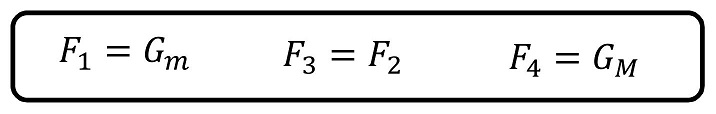
運動方程式を詳しく理解しよう
さて、ここまで来て最後に運動方程式を書き下してみよう。
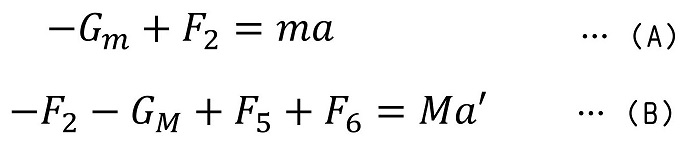
今回の運動は、最初に机と玉は静止しているという前提とともに始めたね。だから、運動方程式をたてたは良いけど、実は速度は永遠に『ゼロ』で、加速度も無論『ゼロ』だね。(加速度がゼロ以外だと、加減速いずれかを実施して最初速度がゼロでもいずれ、速度がゼロでなくなるからね。)
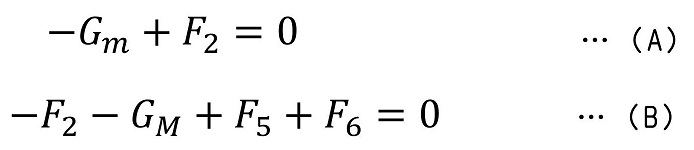
加速度に『ゼロ』を代入すると、(A)と(B)ともに右辺が『ゼロ』になるね。このように、加速度がゼロの時を『力のつり合いの状態』と呼び、(A)や(B)のように右辺がゼロになった式を『力のつり合いの式』と呼ぶよ
さて、重力の大きさが質量によって一意に決まる『わかっている量』とすると、未知数はF2、F5、F6だね。少し整理しようか。
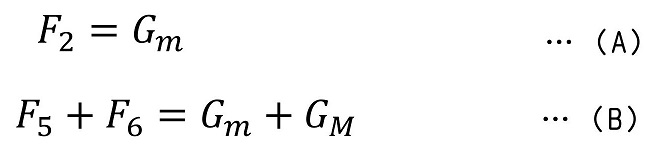
F2まで明確になったよ。あとはF5とF6だ。F5とF6は数学的に求めることは不可能だ。(式1つに対して未知数2つ)解くためには、机という物体や玉のおかれた位置に対称性などの条件をつけることが必要だね。もし机の形状や重さが左右対称であり、玉も机のちょうど中央に置かれているとすると、F5=F6となるね。今回はこれを採用しよう。
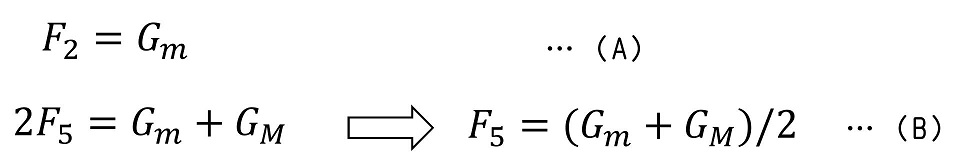
(A)の式について
F2およびF3は玉が机を押す力およびその反作用だよね。この力の大きさが玉自身の重力と等しいということだね。つまり、地球が玉を引っ張ることによって玉に重力が働き、その重力分の力で机を押し、反作用で玉が机から押し返されているわけだね。その結果、玉に働く力は上下つり合った状態になって、加速度がゼロになる、つまり静止するわけだ。
(B)の式について
F5は机の左側の足に働く力で、F5=F6を前提としているため、右側の足にも同じだけの力が加わるね。F5とF6の力を合わせると、Gm+GMになるわけだ。机の脚は、机自身とその上に載っている玉に働く重力を支えているはずだから、机の両脚に働く力が合わせてGm+GMなのは妥当だよね。机に働く力も妥当だから、静止すなわち力のつり合い状態になっているわけだ。
まず重力を考えればよいね。それ以外にも、接触している箇所には力が働くと考えればよいね。軸は先ほどと同じく上向きで地面を原点としようか。
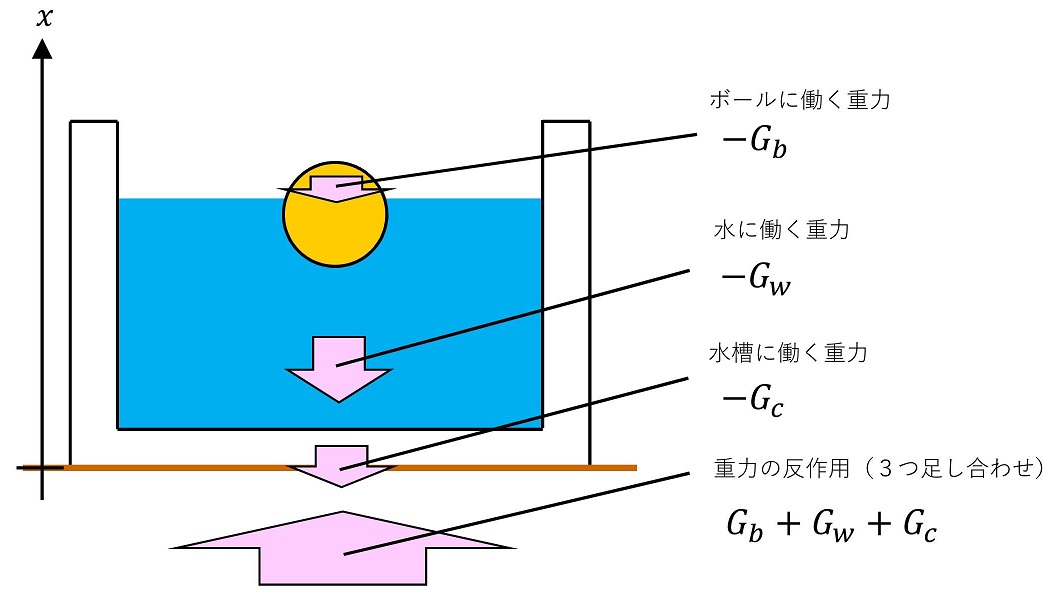
最初に決めた軸と同じ向きを『正』として重力を書き加えたよ。
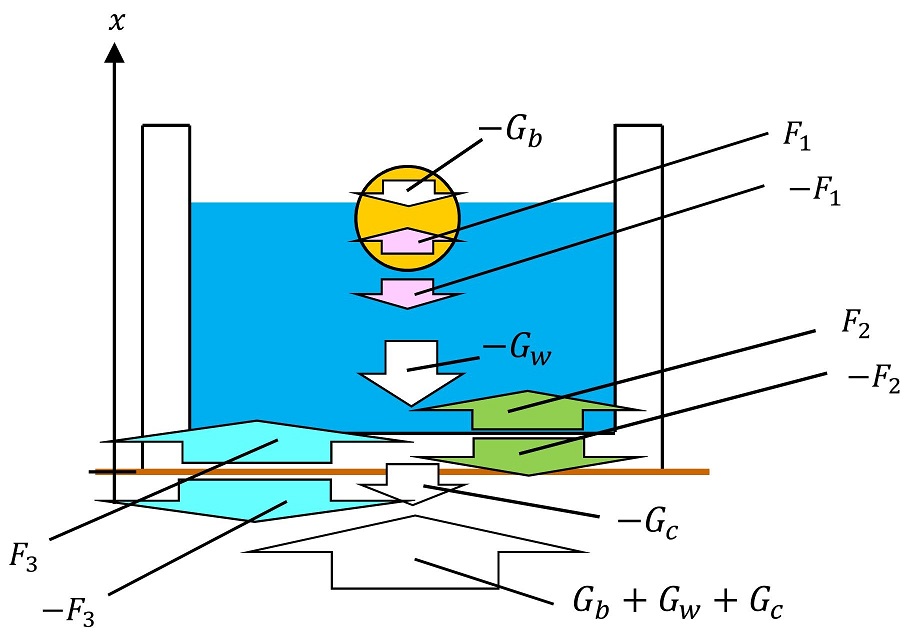
ボール⇔水の間、水⇔水槽の間、水槽⇔地面の間で接しているため、その間に働く作用、反作用を記入したよ。これらの大きさを未知数として求めればよいわけだ。運動方程式を記述しよう。静止しているため加速度は『ゼロ』だね。
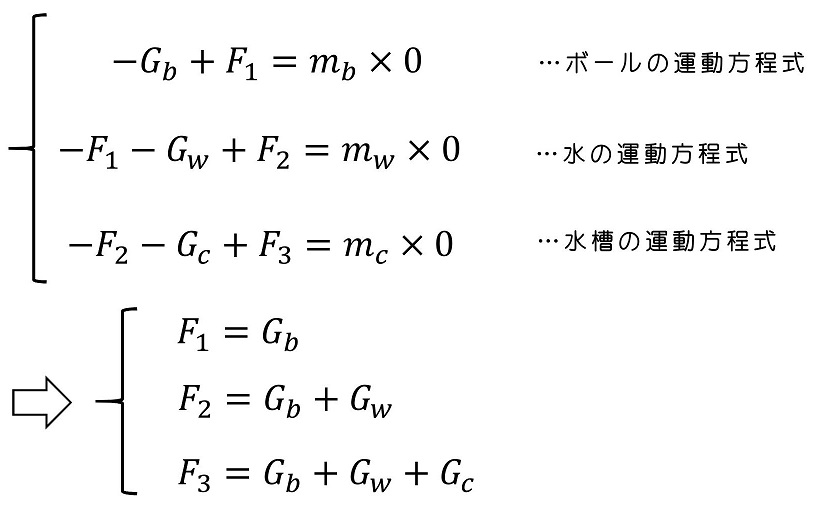
地面にかかる力はF3だから、地面にはボール、水、水槽の3つの重力の合計がすべてかかっているわけだね。
(3)力が釣り合っている運動その2
その1では静止している物体に働く力が釣り合っているという例を紹介したね。実は、物体が動いているときも、力が釣り合っていることはあり得るんだよ。一つ例を紹介しよう。
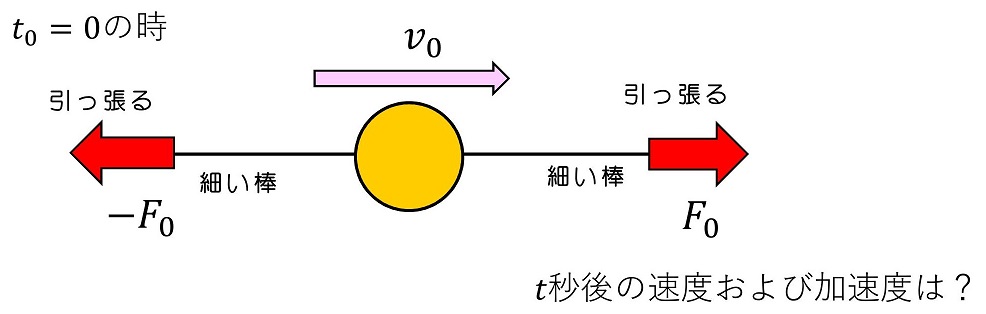
図のように、玉の両端に棒をつけて右端を常に一定の力で右に引っ張り、左端を常に一定の同じ大きさの力で左に引っ張る。初期の速度がv0とすると、時刻t秒後の速度および加速度と位置はどうなるか?
軸を決めよう!
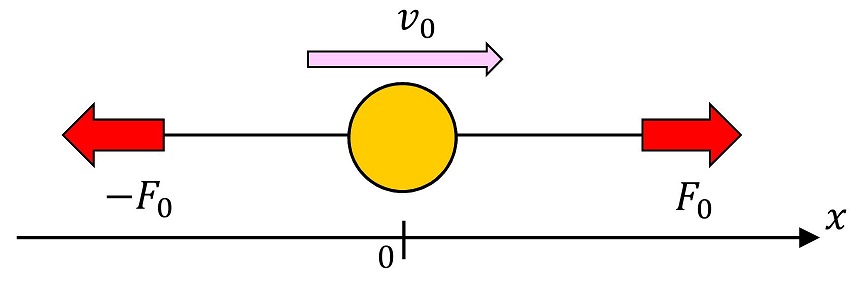
力が加わっている向きは横向きであり、初速も横向きだから、物体はこのまま横方向に運動していくと予想されるね。だから、x軸としては横向きにとってみよう。原点はどこにとってもよいけど、試しに初期状態の時の玉の中心位置を原点としようか。
運動方程式をたてよう!
玉および両端の細い棒の合計質量をmとおくよ。その時の運動の方程式をたてよう。

運動を解釈しよう!
力で両側から引っ張っているから、玉は一見加速しそうだよね。でも今回は、常に左右から『等しい』力で玉は引っ張られながら運動しているため、力は打ち消しあって、釣り合ってしまうわけだ。その結果、働く力はゼロに等しくなって、加速度もなくなるわけだよ。
加速度がゼロとはすなわち、加速しないということなので、速度は常に一定ということになるね。
(4)加速度が一定の運動
最後に、古典力学で最も典型的に取り扱われる運動、等加速度直線運動について議論しよう。
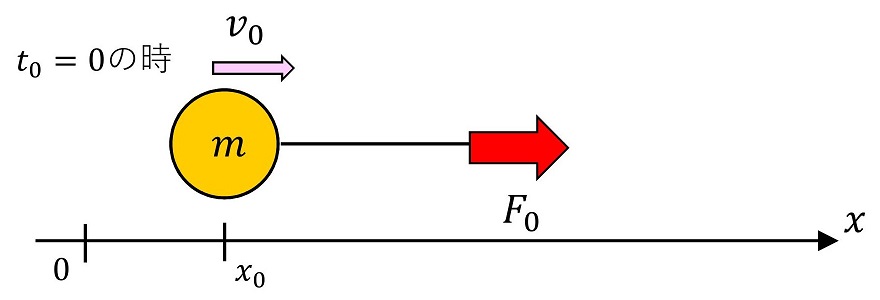
横方向にひもでF0の力で引っ張られている運動だね。ひもの重さは考えず、玉の質量がmとするよ。F0は時間によらず一定だ。つまり、玉を引っ張る人も玉と一緒にどんどん前に走って行っているイメージだね。
軸を決めよう!
動く方向が横方向のため、x軸を横方向にとろう。原点は適当な位置にとろう。初期状態の時、位置はx0にいて、その時の速度をv0としよう。
運動方程式をたてよう!

F0もmも一定値であるため、aも一定の値になるよ。この値をa0とおこうか。
力F0が大きければ加速度a0も大きくなるわけだね。これは直感に合致しているね。引っ張る力が強ければ強いほど、玉は強く引っ張られるわけだから、非常に力強く加速するはずだよね。逆にmが大きければ大きいほど、加速度a0は小さくなるね。つまり力が加わっても、質量が重いほど玉はなかなか動かず、加速しにくくなることを表しているね。
運動を解釈しよう!
ここからの議論が等加速度運動の醍醐味だよ。今まで行ってきた議論では速度と加速度の定義式から、運動の様子を明確にしたわけだね。
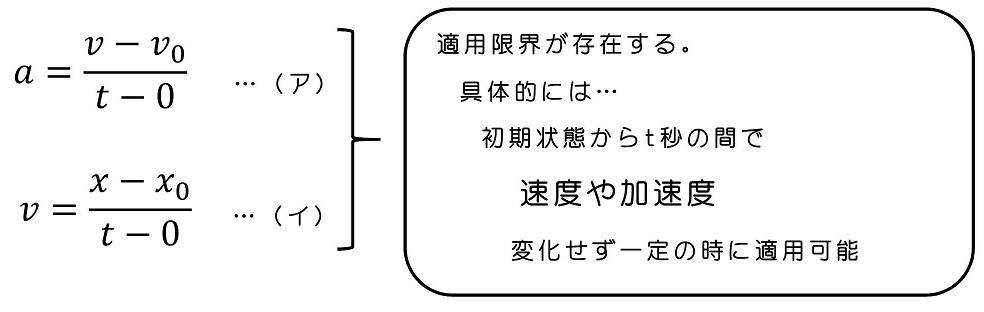
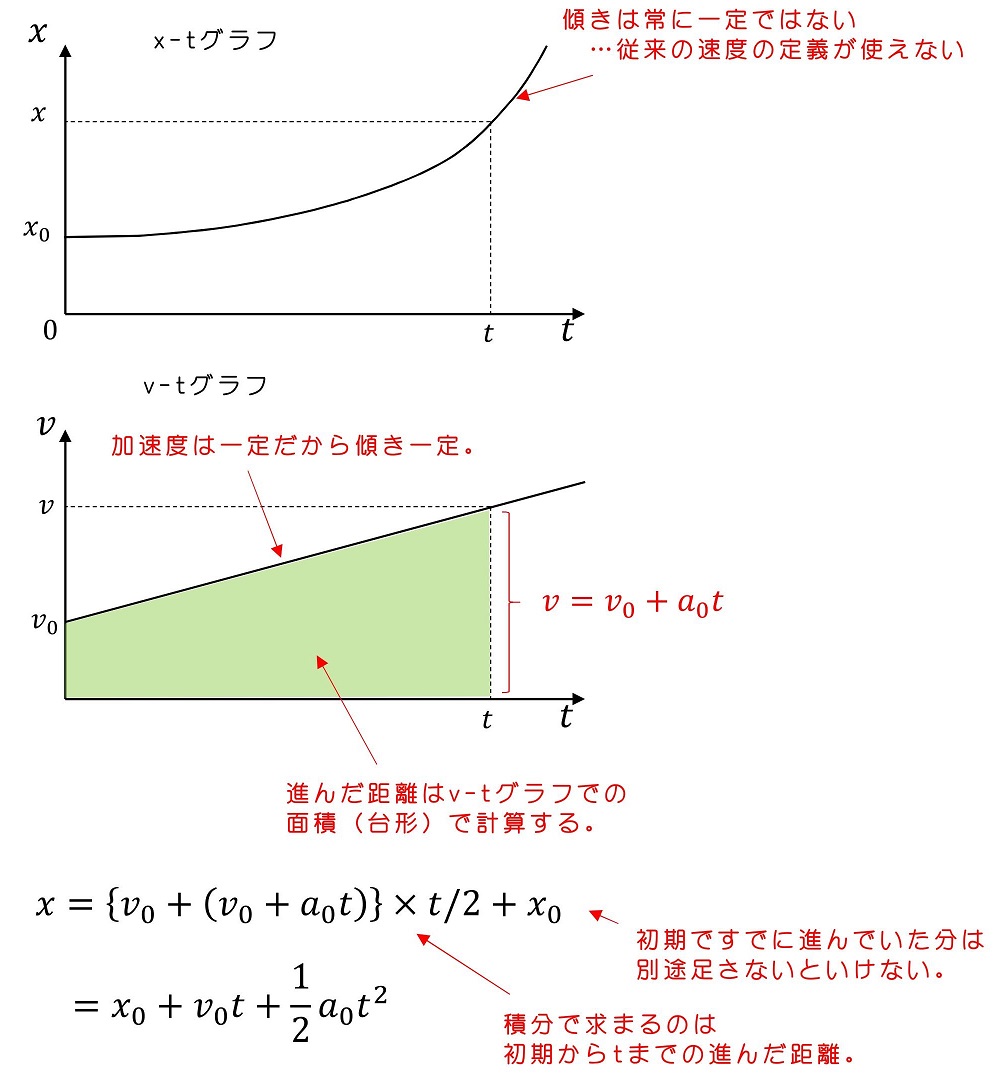
だが、実はこれら定義式には適用できる運動の限界が存在するわけだ。t0~t1の間で(今回の例では時間0~tの間で)速度や加速度が変わらず、必ず一定の時に使うことができる式なんだ。今回の例では加速度は一定だが、速度は一定ではないね。(どんどん加速していく)よって、(ア)式は良いけど(イ)式が適用外になるわけだ。
<適用できない理由をもう少し詳細に>
最初に速度や加速度を定義したときに立ち返ろう。まずは速度からだ。自分の家から学校まで歩くときの速度を考えたんだったね。
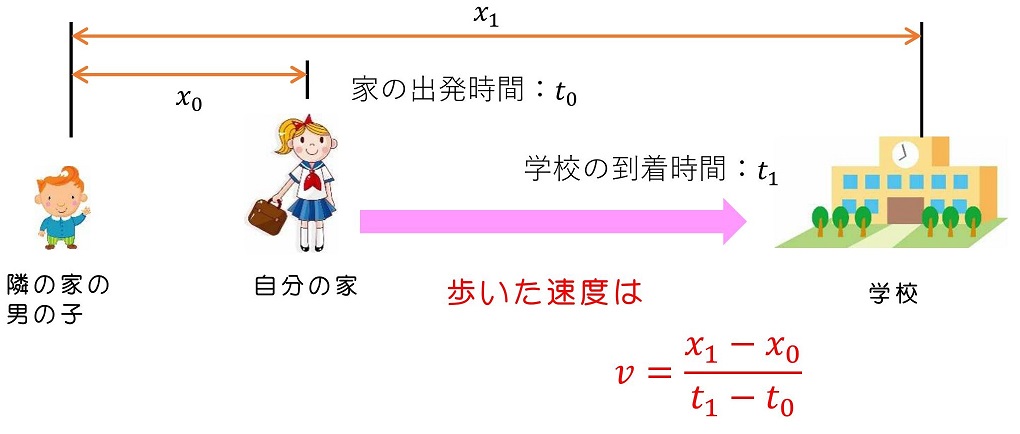
すなわち、自分の家から学校までの距離と、かかった時間の比で速度を表したんだね。だが、少し考察してみよう。家を出てから学校に到着するまでの間に、バスにのるかもしれない、電車にのるかもしれない、歩いている途中に信号で立ち止まるかもしれない。常に同じスピードで進み続ければ、家を出てから学校につくまでのどのような場面でも速度一定なわけだけど、実際は緩急をつけながら歩いているはずだよね。
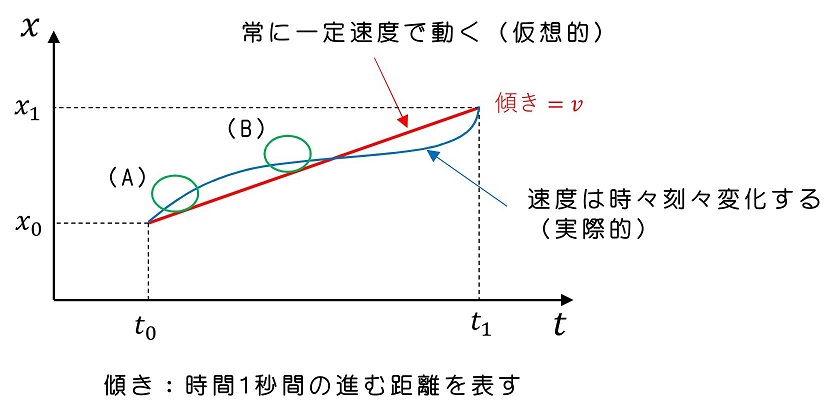
このようなグラフで物体の現在位置を表すことができるよ。これをx-tグラフと呼ぶよ。今まで式で表しているのは、赤い直線のように動いている場合だったんだ。この時、傾きが速度を表すことがわかるよね。
一方、実際的には時間が進めばそれに比例して現在位置も進んでいくわけじゃなくて、ある時には少しの時間で速く進めるが(A:傾きが急)別の時には時間がたってもほとんど進まないときもあるよ(B:傾きが緩やか)ね!つまり、実際の動きは青い曲線のようになるわけだ。
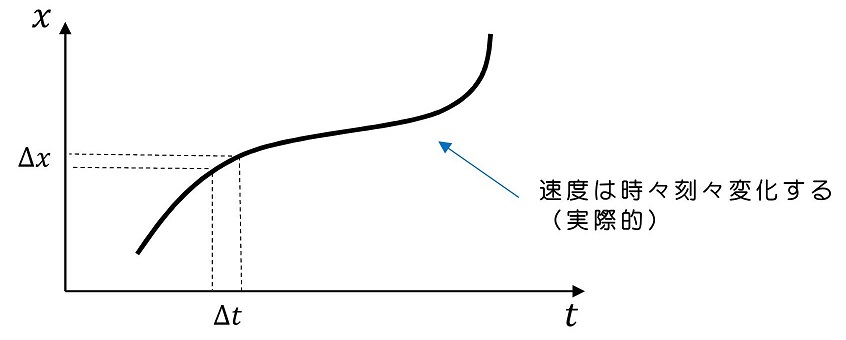
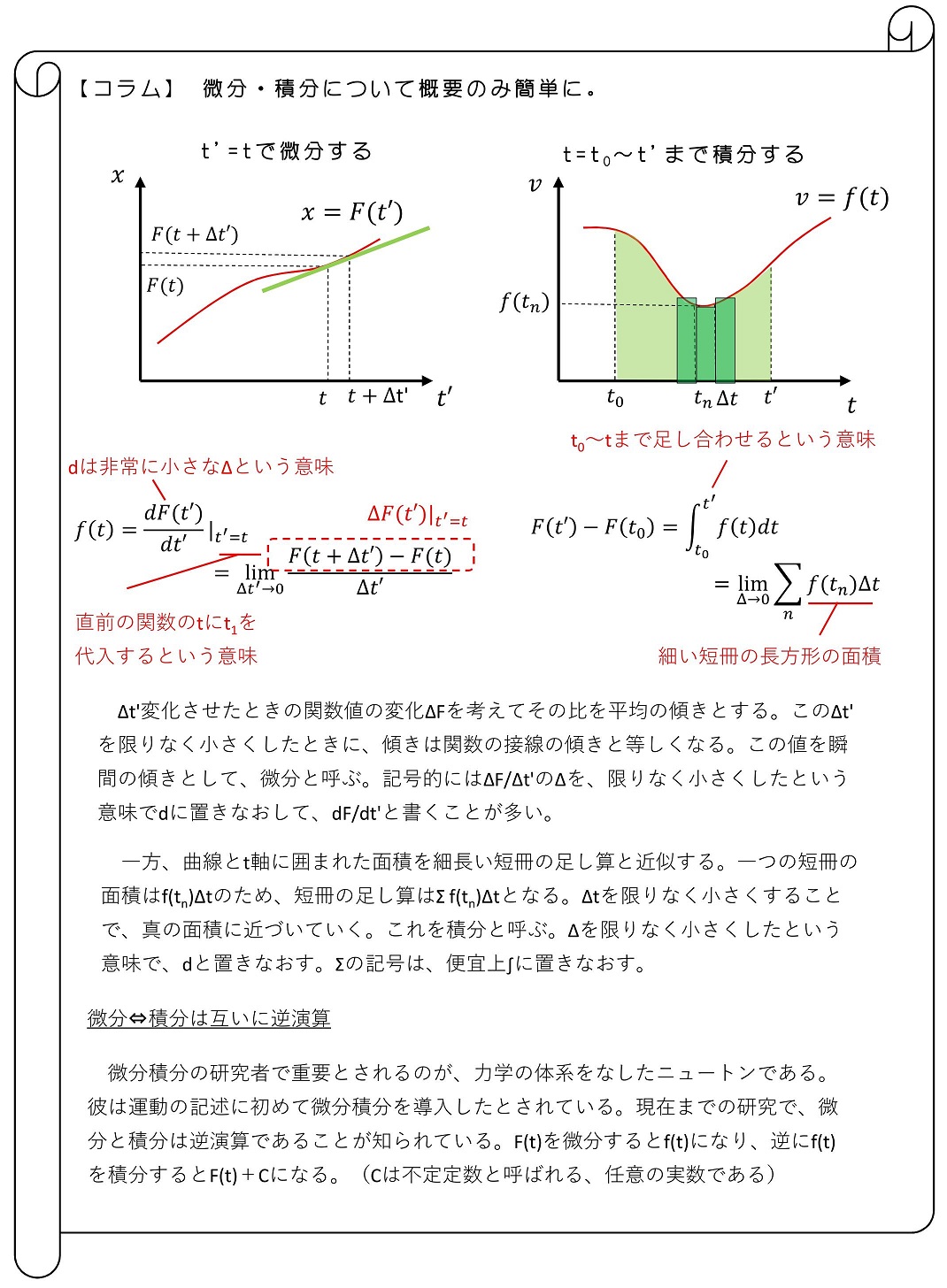
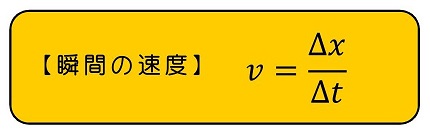
さて、このように速度が時々刻々と変化するような運動の場合、速度をどのように定義すればよいか。重要なのは『非常に短い(※1)』時間間隔Δtを考え、その間の位置変化Δxより速度を求めるという考え方だ。このように定義された速度を『瞬間の速度』と呼ぶよ。

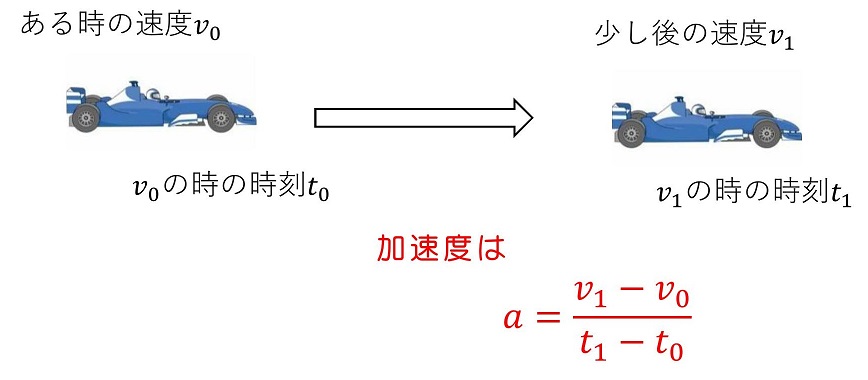
次は『瞬間の加速度』について定義しよう。もともと加速度は次のような例で考えていたんだったね。
瞬間の速度を考えたときと同様にグラフを用いて表そう。これを『v-tグラフ』と呼ぶね。スポーツカーは常に一定の加速度で変化しているわけではない可能性があるよ。
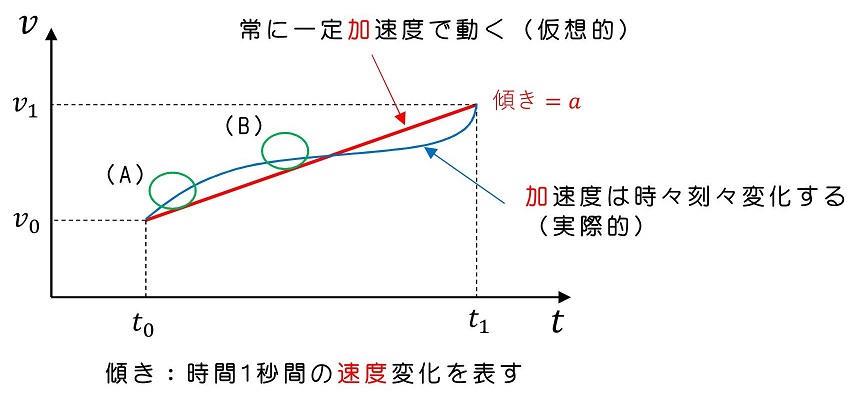
(A)の箇所では非常に激しく速度変化しているから加速度は大きいはずだし、(B)の箇所ではほとんど速度変化しないから加速度は小さいはずだね。
瞬間の加速度を定義するよ。やはり『十分短い時間』の間の速度変化を考えて、その比を瞬間の加速度と定義するよ。

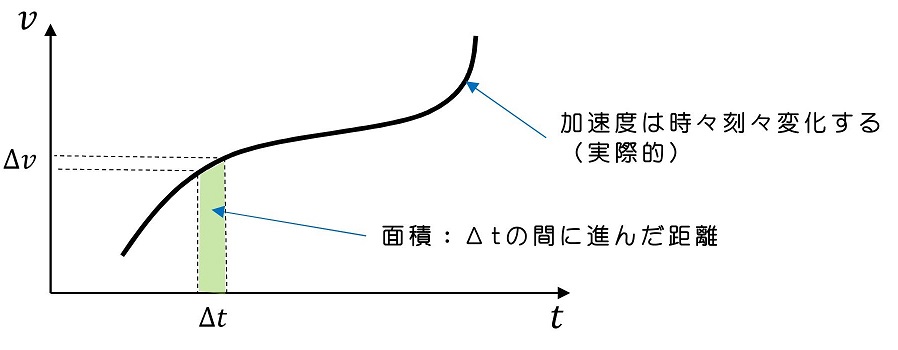
さて、v-tグラフではもう一つ、重要なアイデアも出現するよ。時々刻々と変化する速度のグラフがある時、グラフとt軸でなす面積(※2)は進んだ距離を表しているんだよ。
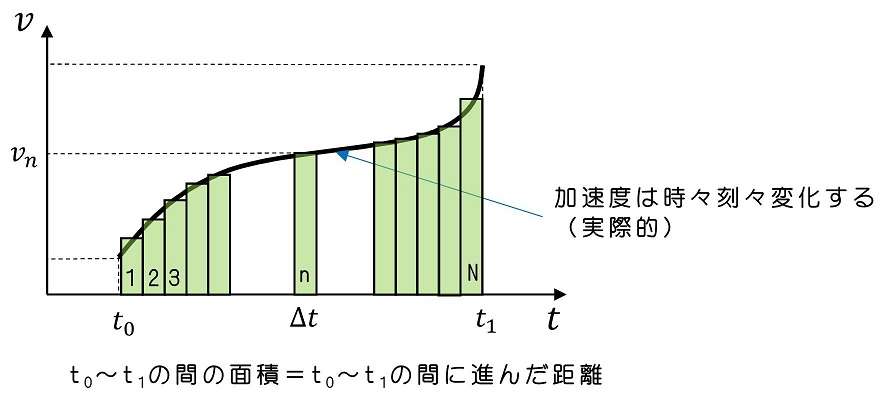
グラフのなす面積を細いN個の短冊で小分けしようか。短冊の面積の合計は、グラフのなす面積に近似できるわけだね。ではn番目の面積について考えてみようか。Δtを『十分小さく』とると、その間vは『ほとんど変化しない』と仮定できるんだよ。
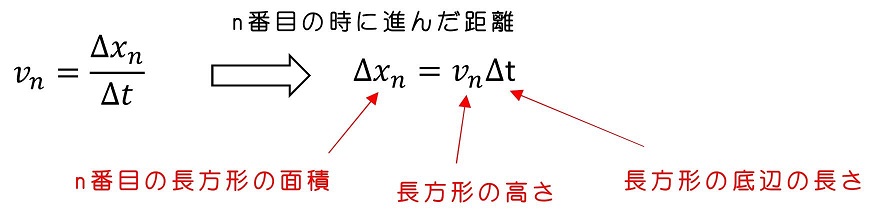
n番目の面積=n番目の時に進んだ距離と、とらえることができるようになるわけだ。長方形を1番目からN番目まで足し合わせれば、t0からt1まで進んだ距離のになるわけだね。

<等加速度直線運動に戻ろう>
経過時間tにおける速度は?
加速度一定の運動なので、この場合は瞬間の加速度の定義を使わなくても、従来の定義式から速度を求めることができるよ。

経過時間tにおける進んだ距離は?
初期から経過時間tの間で、速度は一定ではないから、従来の定義から現在位置を求めることはできないよ。v-tグラフを書いて、その面積から進んだ距離を求めるのが妥当だね。