4.1 重力下での物体の運動
地球上に存在するすべての物体には重力が働くよ。重力=地球との間の万有引力であるため、地球中心からの距離により大きさが変わるが、地球の半径が6500kmほどあるため、100mオーダーのビルまでの高さであれば、万有引力はほぼ一定とみなすことができるよ。地球表面付近で働く地球からの万有引力のことを、重力と呼ぶよ。
ビルの上から玉を落としたり、真上に投げ上げたり、斜めに打ち出したりしたときの、玉の運動はどのようになると推測できるだろう?すべて、重力のみが働くよ。この章で議論するのは、このような重力下での運動だ!
4.2 自由落下
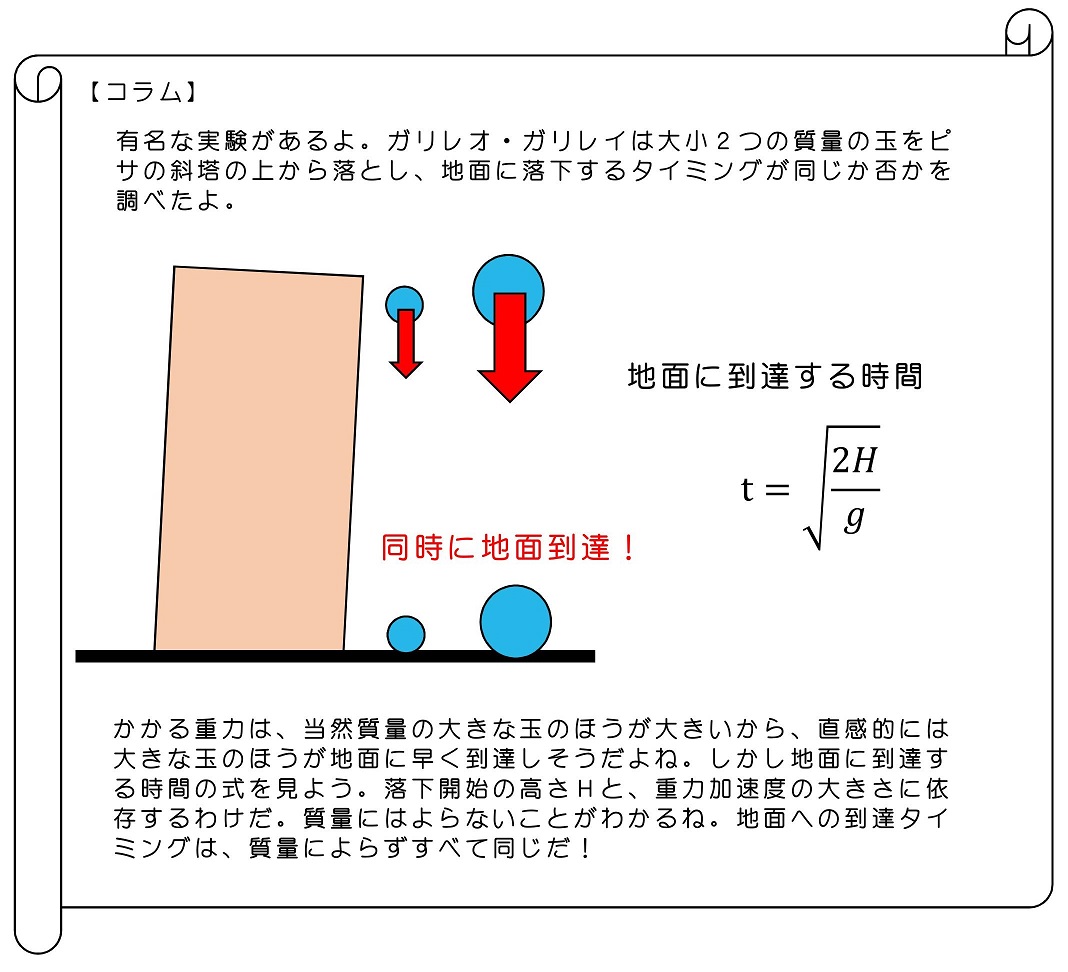
ビルの屋上からそっと手を伸ばし、その手に持っている玉を、地面に向かって静かに放そう。玉はどのように運動するだろうか?具体的に、t秒後にはどれだけの距離落下し、何秒後に地面に到達するだろうか?地球重力下における落下運動を自由落下と呼ぶよ。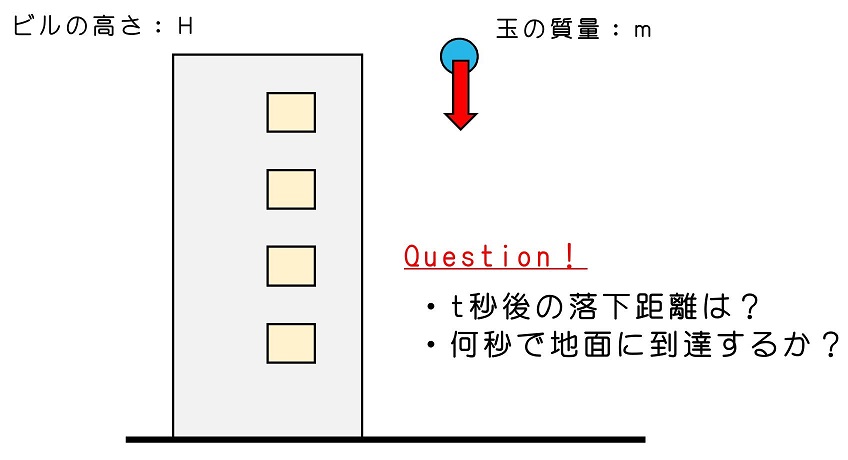
①運動を予想しよう
玉は最初静かに放されるようだね。つまり、最初の速度はゼロだ。ただ、玉には下向きに重力がかかるため、下向きに加速してゆくよ。最終的には、地面に到達するね。
②運動の軸を決めよう
運動の軸を決めるときに重要なのは、予想される運動を記述しやすいことだよ。原点を地面に、上向きにx軸の正の向きをとってみよう。
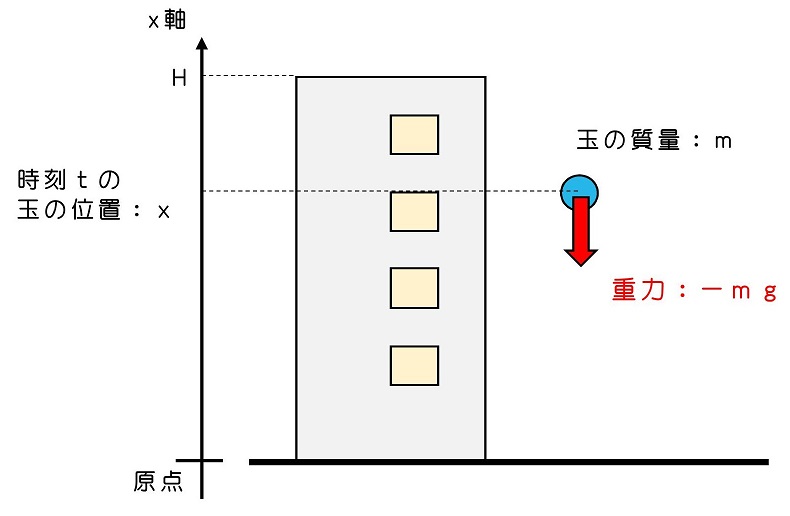
③玉に働く力を整理して、運動方程式をたてよう
玉に働く力は重力のみであり、働く向きはx軸と逆向き、すなわちマイナス方向だよ。
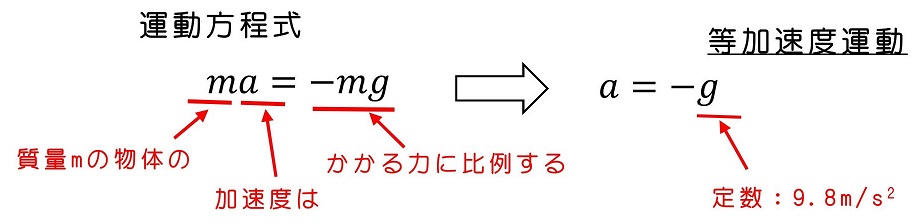
知りたいのは、このような等加速度運動をしているときの、t秒後の速度や玉の位置になるわけだ。どうやって導けばよいか?公式を覚えておくのも一つの手だが、実は積分をすることによって、容易に公式それ自身を導くこともできるんだよ。
<公式を使う場合>
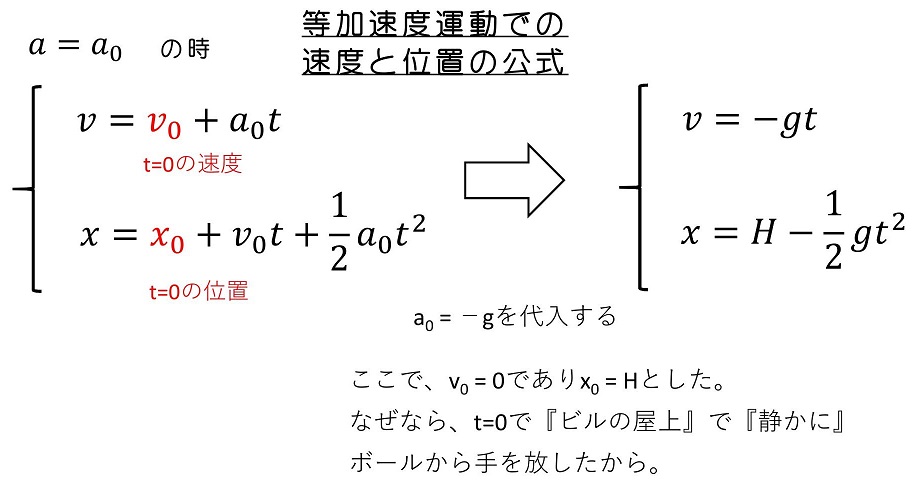
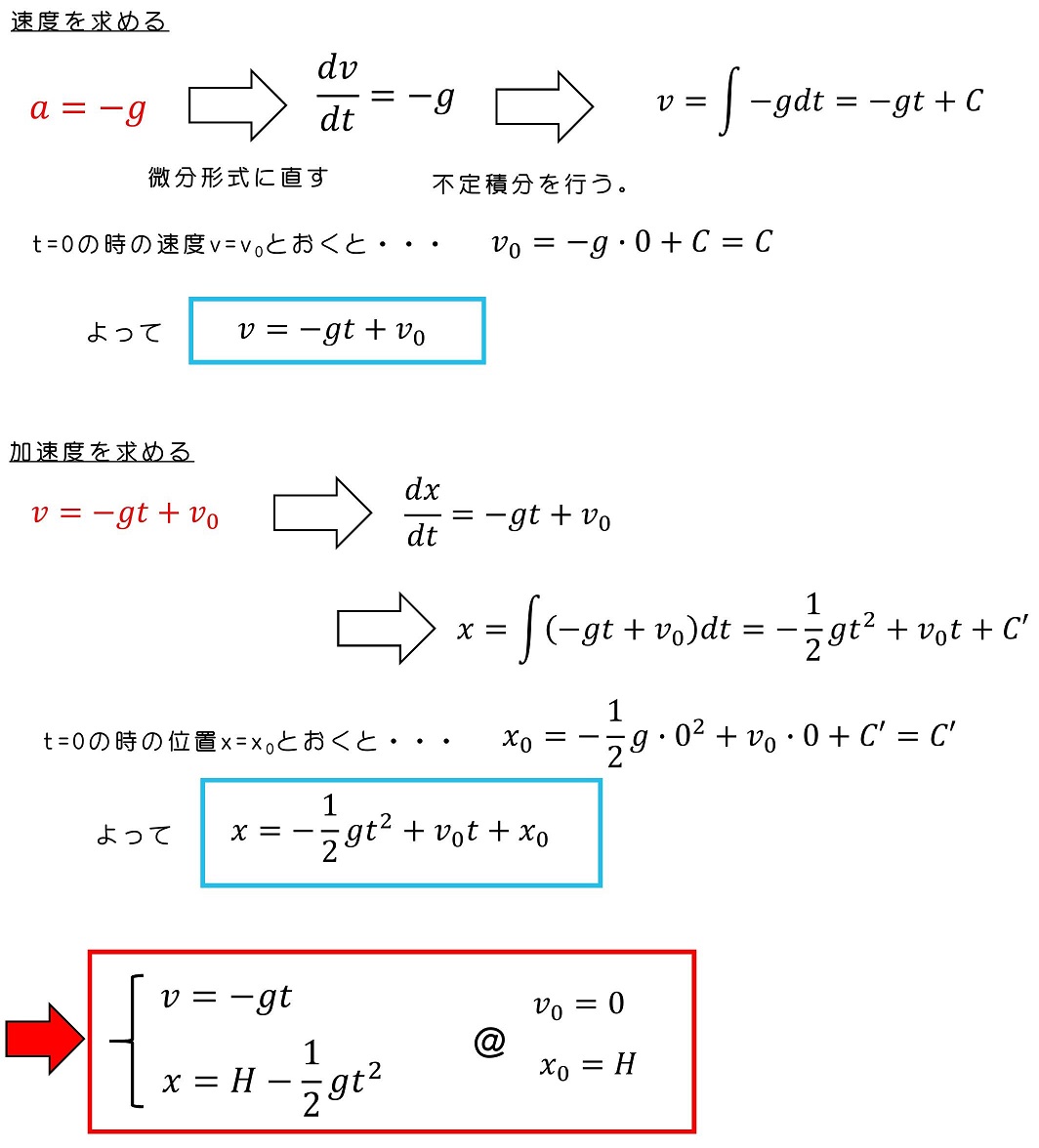
<積分する場合>
速度とは、位置の時間での微分、加速度は速度の時間での微分になるよ。これを瞬間の速度、瞬間の加速度と呼ぶよ。

Δt経過したときに、Δx位置が変化する。この時のΔx/Δtを『平均の速度』と呼ぶ。Δtは1時間でも10分でもよいが、ここではどんどん短くしていこう。1秒、0.1秒、0.01秒・・・とどんどん短くして、理論上無限に小さくしていった時の時間経過をdtと書き、その時の位置の変化をdxと書く。 dx/dtを『瞬間の速度』と呼ぶ。これは数学的には関数x(t)をtで微分したのと同じ意味だ。

加速度も同様の議論ができる。微分で表した形式を瞬間の加速度と呼ぶ。
④運動を表す式を解釈しよう
落下開始からt秒後の落下距離はいくらか?を求めよう。
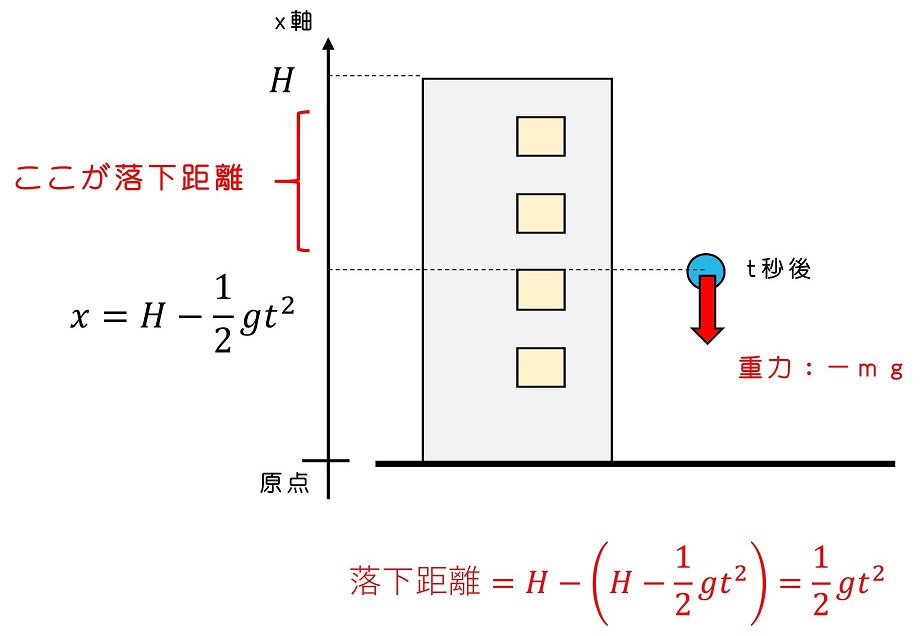
何秒で地面に到達するか?を求めよう。
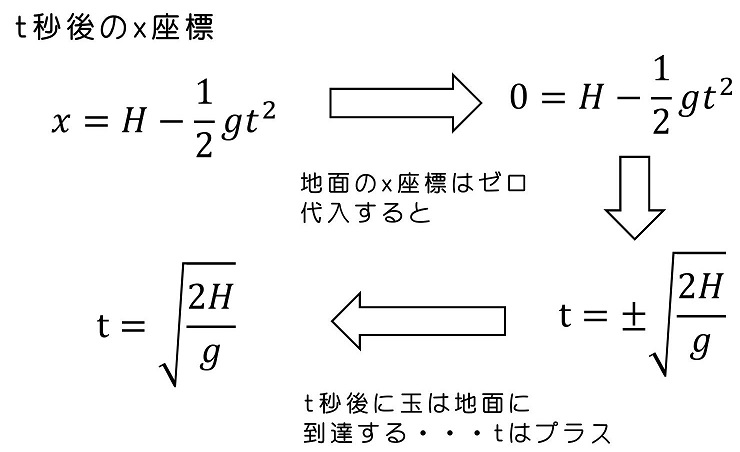
4.3 鉛直投げ上げ
ボールを手にもって、真上に投げ上げた場合の運動を考えよう。きっと、ある高さまで飛んで行ったあと、まっすぐ落ちてきてもう一度自分の手に収まるよね。最高到達高さおよび、投げ上げてからもう一度落下して手に収まるまでの時間を求めよう。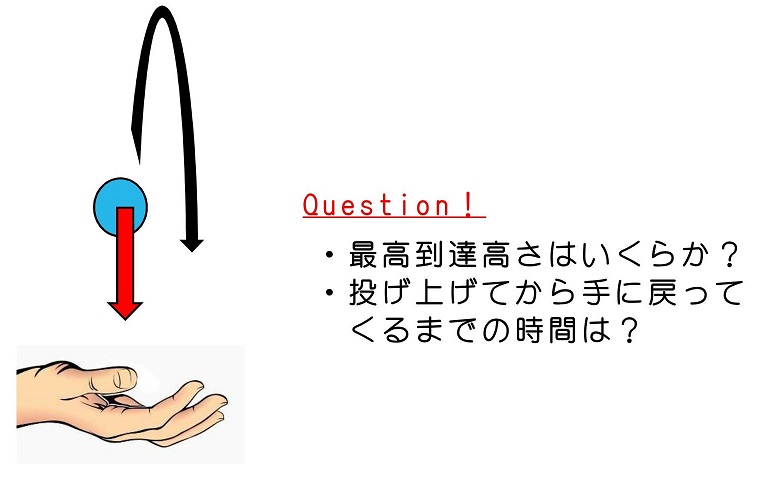
①運動を予想しよう
真上に投げ上げた後、速度は重力によってどんどん落ちてゆき、いったん速度がゼロになるね。そのポイントで最高到達点を記録し、次の瞬間で最初と逆方向(手に戻ってくる方向)に運動を開始し、重力によって加速しながらやってきて、最終的に手に収まるはずだよ。
②運動の軸を決めよう
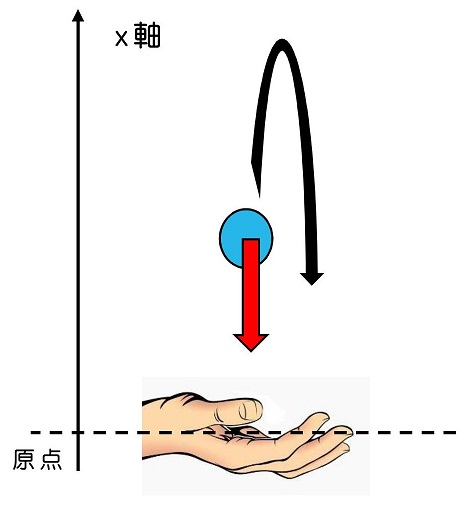
今回、上下のみの運動なので、上下方向に軸をとればよいね。原点及び軸の向きは、きみの好きなように決めればよいが、今回は投げ上げた瞬間の手の位置を原点とし、上方向にx軸をとろう。
③玉に働く力を整理して、運動方程式をたてよう
働く力は再び重力のみだ。x軸のプラスの向きを上向きにとっており、重力は下向きに働くのでマイナスだ。

積分定数を決めねばならないね。t=0の時の速度と位置を整理しておこう。手を放した瞬間をt=0とするよ。手を放したとき、玉は所定の速度で上向きに運動しているよ。これをv0とおこう。また手を放した瞬間の位置を座標の原点とするため、t=0の位置座標はx=0となるよ。

④運動を表す式を解釈しよう
最高到達高さを求めよう。①で運動についてイメージできていれば、速度の式を用いて容易に解くことができるよ。

あるいは、数学を用いて、式を解釈してもよいよ。いきなりxの式から取り掛かろう。
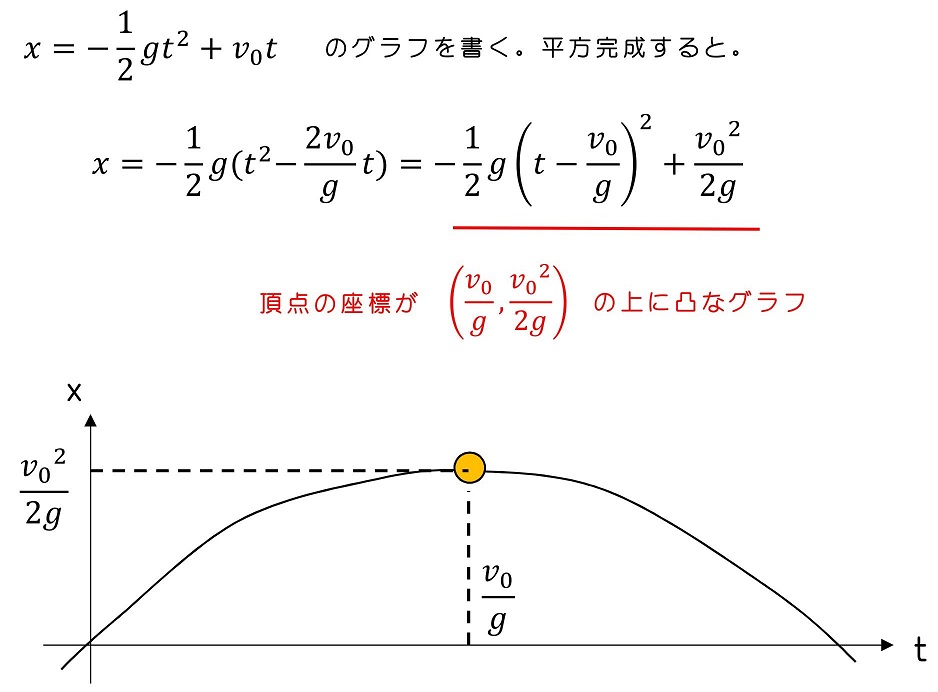
横軸がt、縦軸がxだね。いろいろな時刻ごとの、高さxがわかるよ。高さが一番大きくなるのは、時刻がv0/gの時で、その時の高さはv0^2/2gとなることがわかるね。
投げ上げてから、手に戻ってくるまでの時間を求めよう。運動についてイメージできていれば、容易に求めることができるよ。
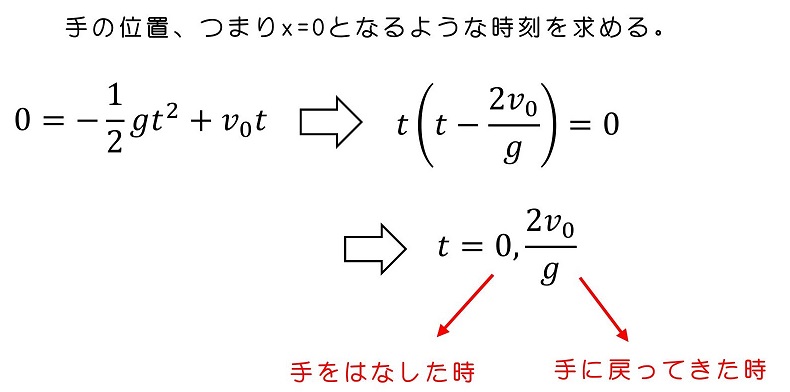
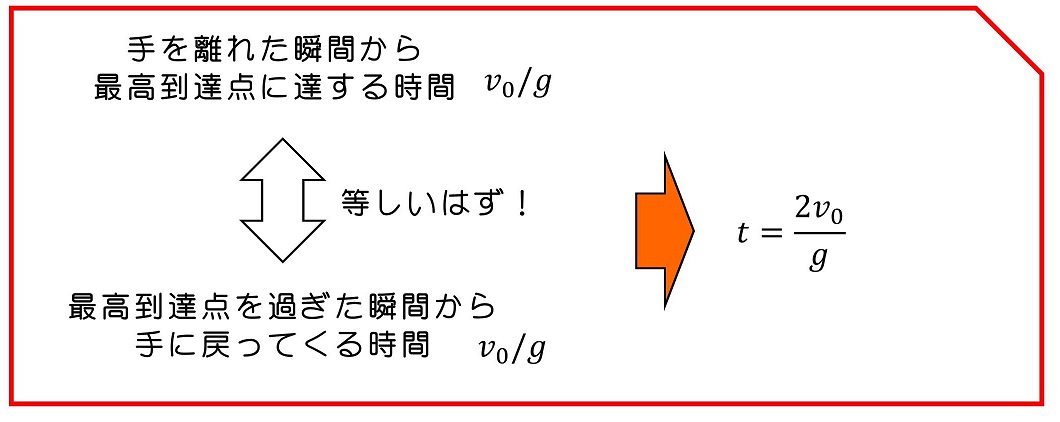
さらに、運動について深い理解をしていれば、一瞬で求めることができるよ。
4.4 鉛直投げ下げ
地面に向かって、ボールを投げつける運動を考えよう。自由落下と異なるのは、手を離れた初速がゼロでないこと。鉛直投げ上げと異なるのは、初速が上向きでなく、下向きであることだよ。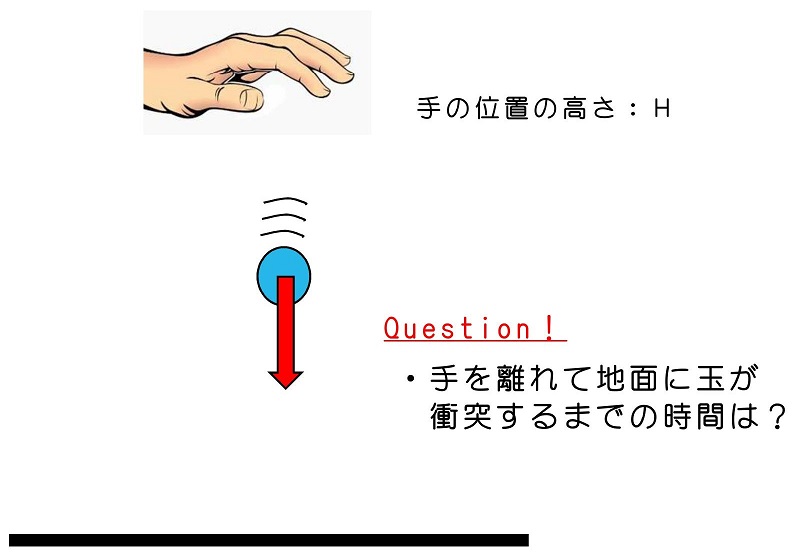
①運動を予想しよう
まずはやはり、運動を予想するところから始めよう。手をある速度で離れた直後、重力によって下向きの速度はどんどん加速していくね。その結果、相当早いタイミングで地面に衝突するだろうね。
②運動の軸を決めよう
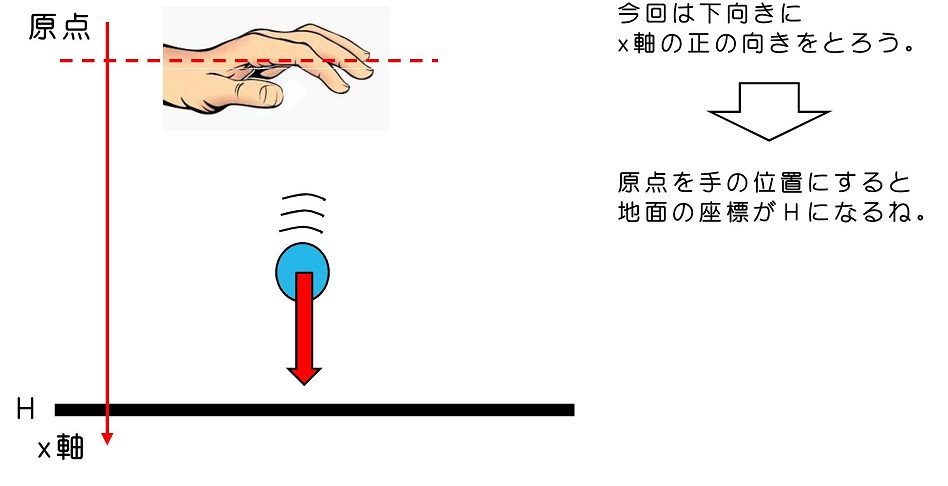
③玉に働く力を整理して、運動方程式をたてよう
下向きをx軸のプラスにとったよ。重力も下向きなので、重力もプラスにして運動方程式を作るよ。

④運動を表す式を解釈しよう
地面についた時間を求めよう。x=Hとなるような時間を求めればよいよ。

2次方程式の解の公式を使うと、tは次のようになるよ。
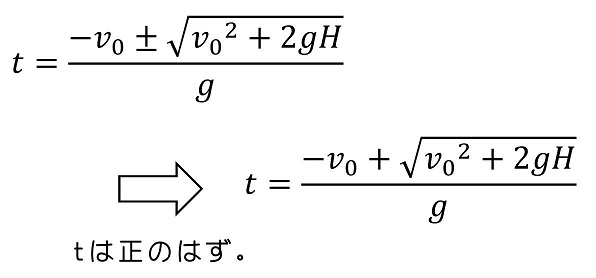
4.5 斜方投球
さあ、ここからワンランクUPした問題になるよ。斜め上方に向かって、ボールを投げることとしよう。投げ上げる角度をθとおくよ。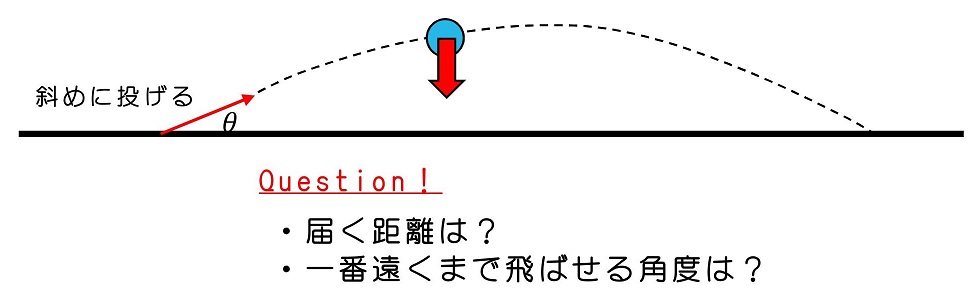
①運動を予想しよう
今まで議論してきた運動では、必ず『力の働く向き』と『運動の方向』が一致していたよ。自由落下も、鉛直投げ上げも、鉛直投げ下げも、すべて重力の向きと同じ方向に運動していたね。射法投球も下向きに重力が働くことは間違いないが、運動は重力方向と一致せず、斜めに動くよ。
横向きに働く力がないから、速度のうち横方向には加速も減速もしないはずだよ。一方縦方向には重力が働くよ。最初はどちらかといえば上方斜めに運動するけれど、重力によって上向きの運動が弱められ、最上点では横方向のみの運動になり、いずれ斜め下向きの運動に変わって地面に衝突するよ。
②運動の軸を決めよう
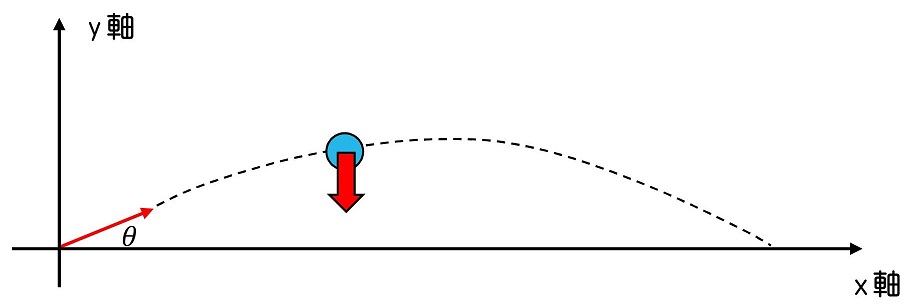
今までの運動で設定すべき軸は、常にx軸一つだけだったよね。その理由は今まで直線状の運動だったからだ。今回の運動は平面的だよね。つまり、運動を表現するためにはx軸とy軸の2つが必要になるわけだよ。
③玉に働く力を整理して、運動方程式をたてよう
運動方程式を解くことによって、運動を記述することができるよ。運動方程式は、運動の3大法則の一つだね。紹介した運動方程式は、すべて加速度も力も1次元であったと考えたけれど、2次元や3次元にも拡張できるよ。

太字はベクトルを表すよ。ベクトルを成分表示したり、連立式として表したりしているが、いずれも等価な意味だよ。もし2次元運動を扱いたいときは、z成分を省略した式だと考えればよいよ。
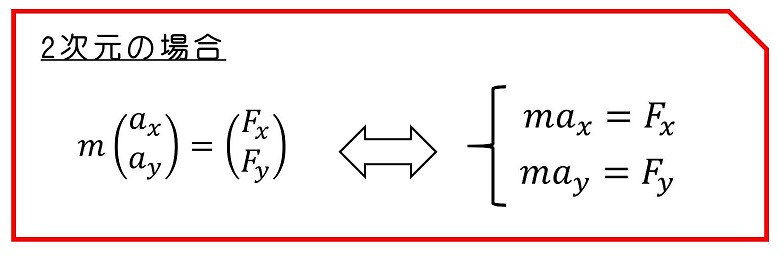
2次元の運動方程式をたてよう。連立式の形がわかりやすいよ。
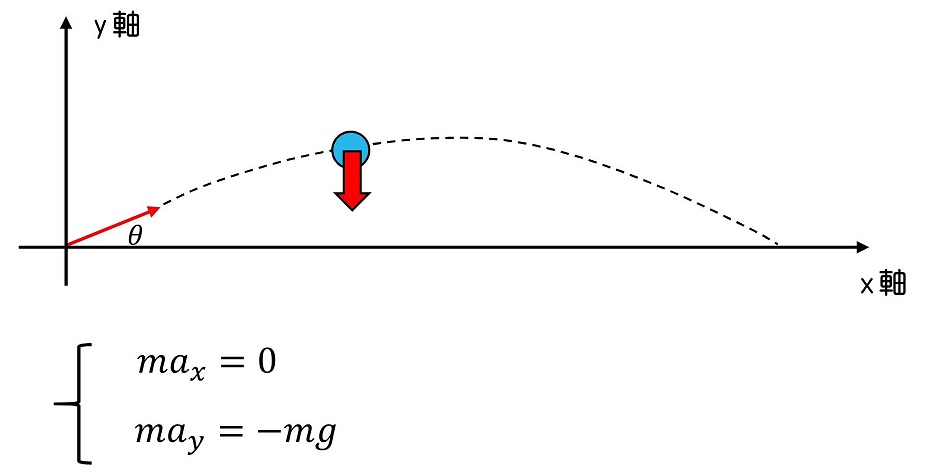
玉に働く力は重力のみであり、これは下方向すなわちy軸のマイナス方向を示している。x軸方向には力は働かない。運動方程式をそれぞれ解いてみよう。積分すればよいよ。
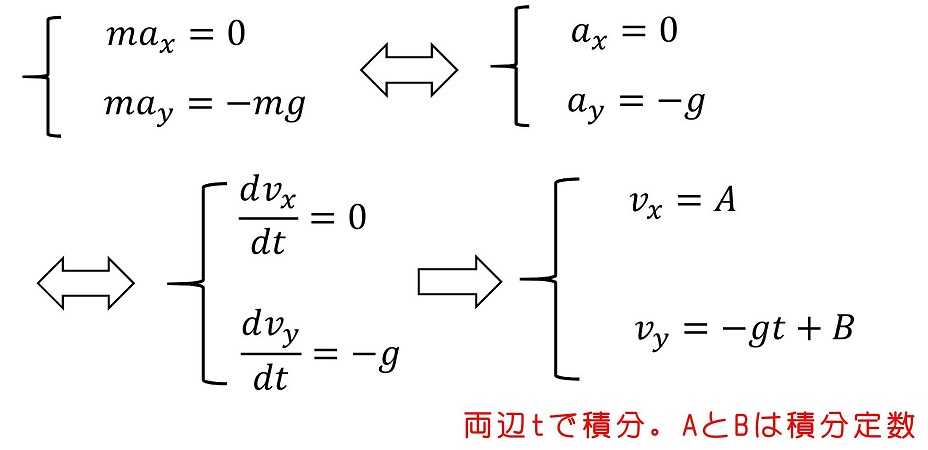
初期状態(t=0)でのx方向、y方向それぞれの初速はいくらだろう?
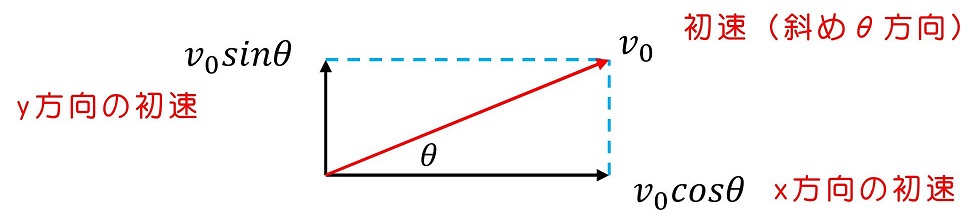
t=0の時の条件から積分定数AとBを求める。
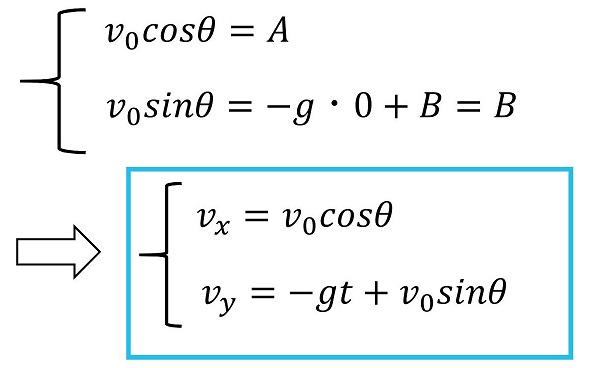
さらに積分して、座標の時間変化を求める。
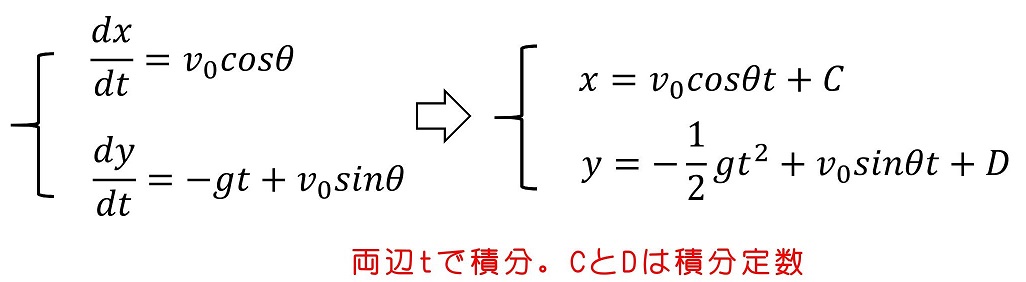
初期状態(t=0)でのx座標、y座標はそれぞれゼロである。
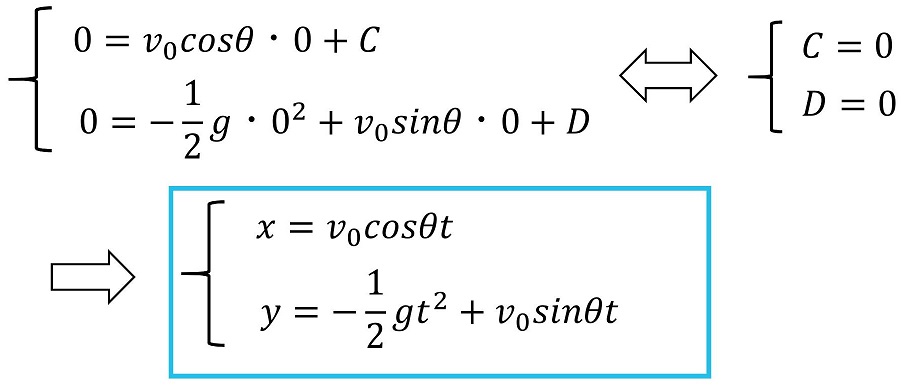
④運動を表す式を解釈しよう
では、果たしてどこまで玉は届くだろうか?
まずは『地面に落下する=y座標がゼロ』という条件を用いよう。

さらに、その間x方向にどれだけの距離進むか調べよう。
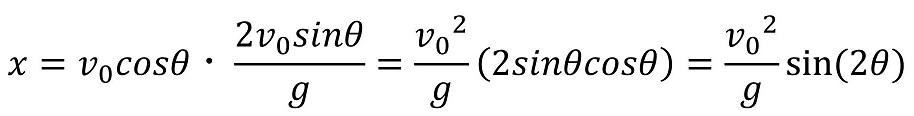
届く距離が最大になるようなθはいくらになるだろうか?斜め前方に投げる場合を考えているので、θは0°~90°の間だ。

4.6 水平投球
2次元運動のもう一つの代表的な問題として、水平投球があるよ。ビルの屋上から、玉を水平に投げるような場合だね。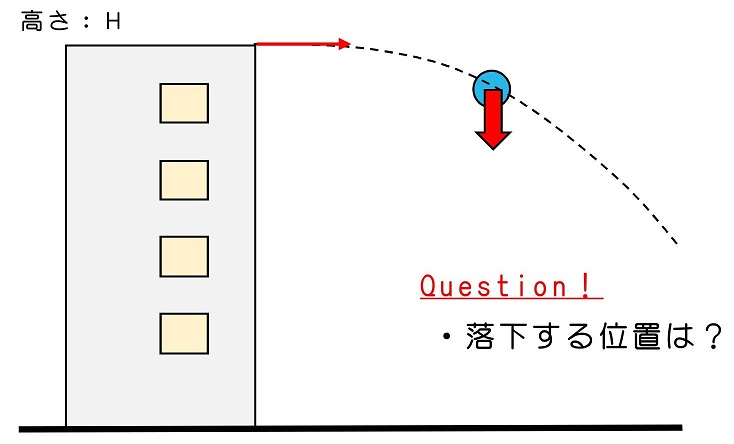
①運動を予想しよう
最初、ビルから真横に投げられることで玉は横方向に飛んでいくわけだけど、重力が下向きに働くため、引っ張られて徐々に、斜め下の方向に玉は動くだろうね。その結果、最終的には地面に落下するわけだ。運動の方向と、働く重力の方向が一致しないため、2次元平面内の運動と予想されるよ。
②運動の軸を決めよう
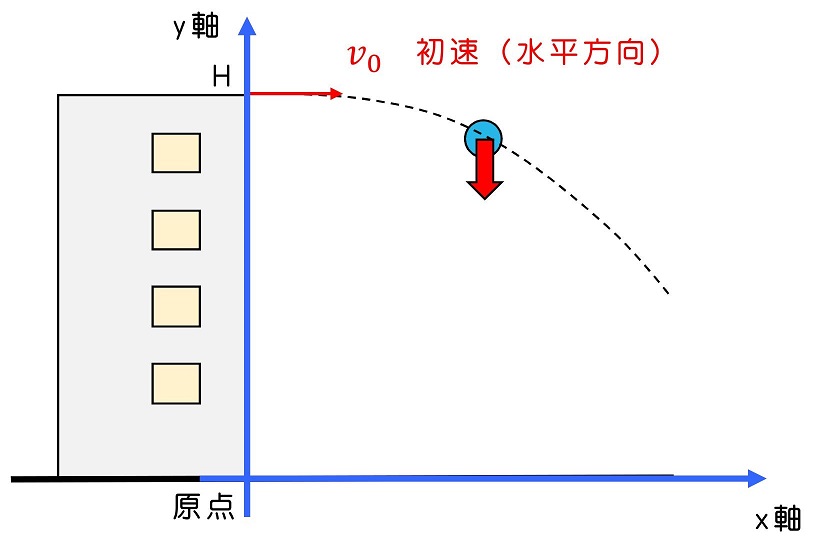
図のように横方向にx軸、縦方向にy軸をとろう。水平投球をを開始したポイントの座標は(0,H)となるよ。
③玉に働く力を整理して、運動方程式をたてよう
2次元空間としての運動方程式になるよ。
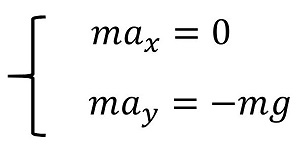
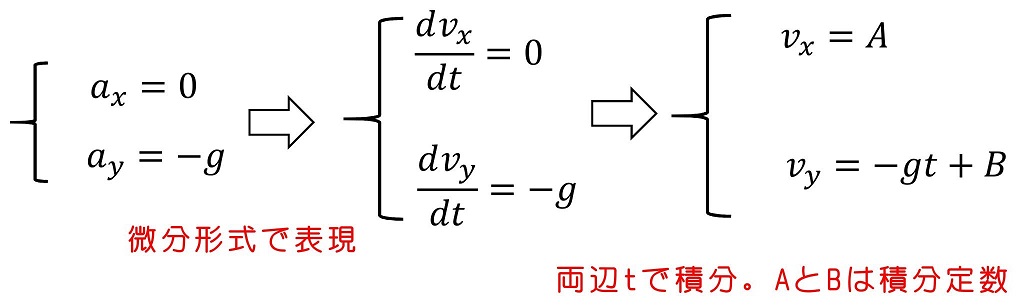
おや?と思う人もいるだろうね。運動方程式が射法投球の場合と完全に一致しているよ。今回は水平投球のはずだ。何か間違えたのだろうか?もう少し解いていってみよう。まずはx方向、y方向ともに質量mで両辺割るよ。
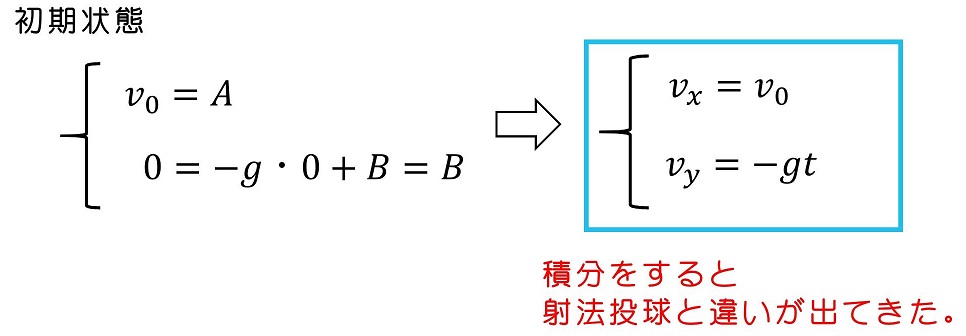
初期状態を考えよう。初速v0で玉は水平に打ち出されるよ。すなわち、t=0でのx方向の速度はv0であり、y方向の速度は0になるね。
さらに積分しよう。
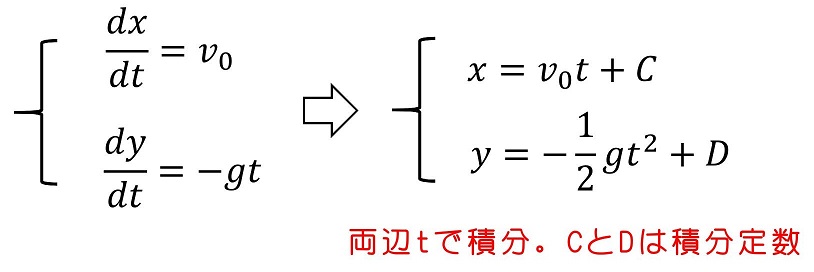
初期状態を考えよう。初期のx座標はゼロだが、y座標はHになるよ。
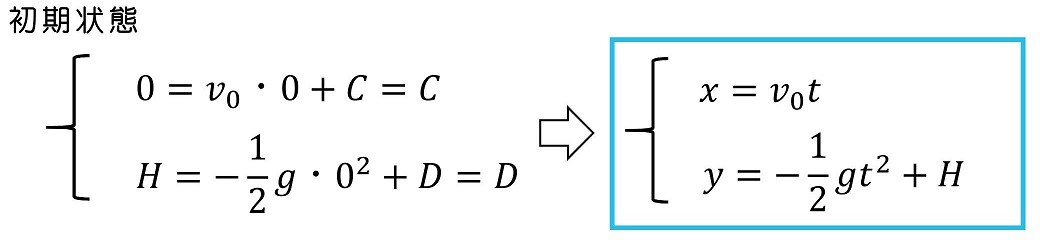
④運動を表す式を解釈しよう
落下する位置は、どこになるだろう?y座標がゼロに達するような 時間は何秒後かを、まずは考えるよ。
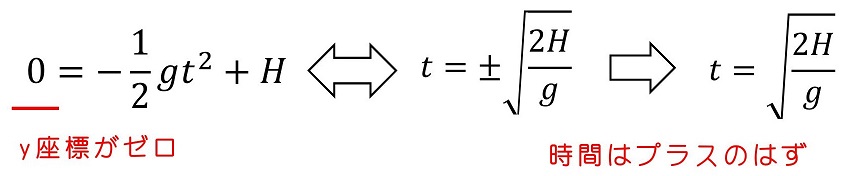
さて、地面に到達するのにかかる時間がわかった。その間、x軸方向にはどれだけ移動するだろうか?x方向の式のtに上で求めた時間を代入すればよいよ。
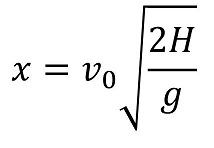
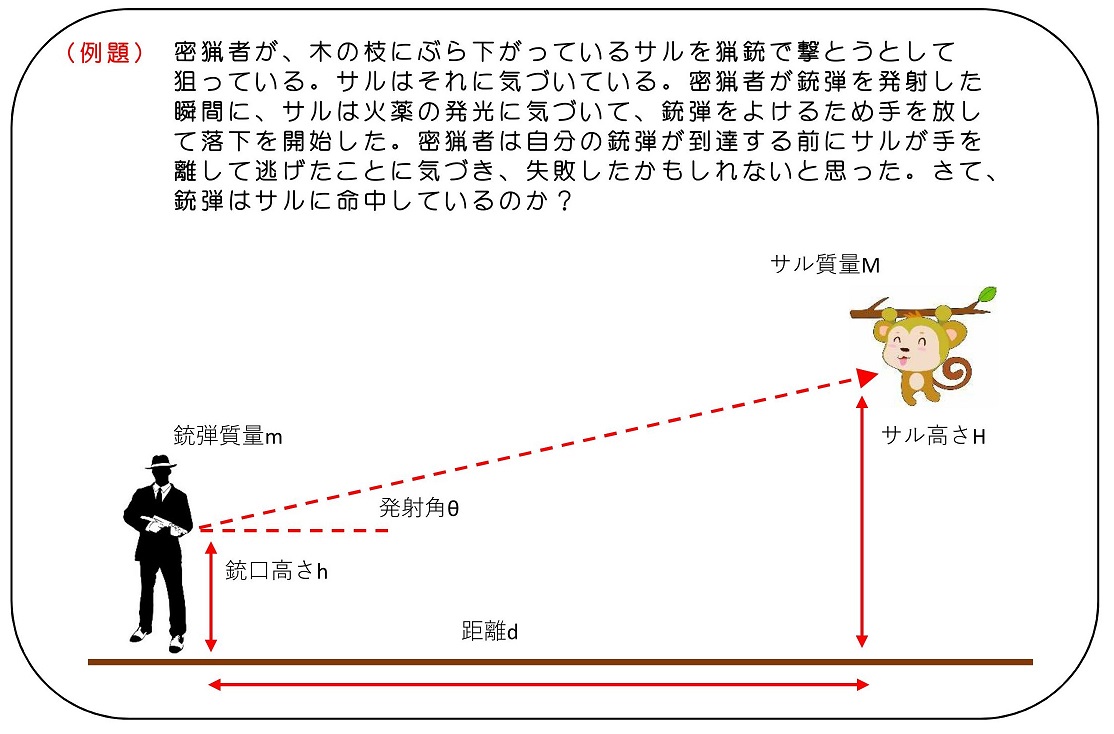
①運動を予想しよう
サルが撃たれていたらかわいそうなため、銃弾が当たっていないことを願いたい。銃弾の飛行もサルの落下も、重力下の物体の運動だよね。運動方程式を用いて、それぞれどのように運動をするか考察しよう。注意すべきは、銃弾にもサルにも重力が働くということだ。銃弾は発射角θの斜方投球の問題になるよ。一方、サルは自由落下の問題になるよ。
②運動の軸を決めよう
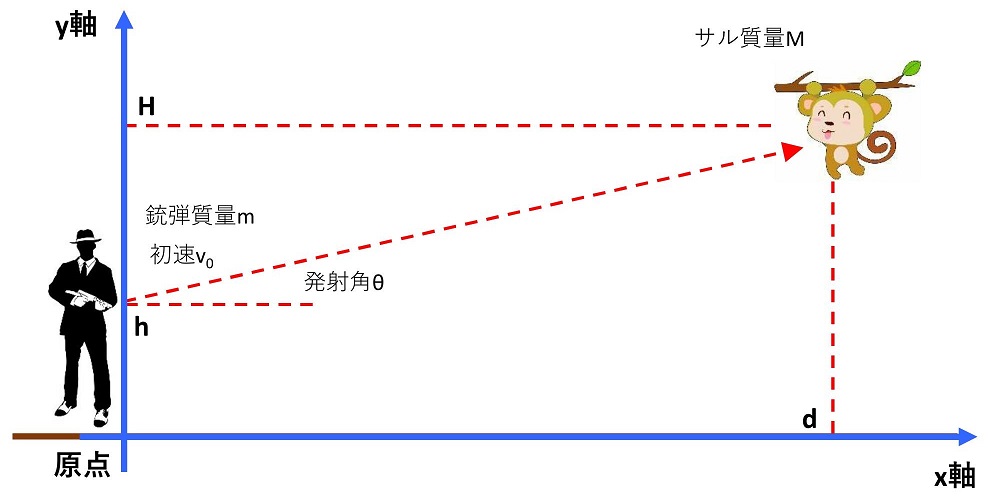
サルは1次元的な運動だが、銃弾は2次元的な運動になるだろう。よって、サル、銃弾共通でx軸とy軸を図のようにとろう。
③運動方程式をたてよう
銃弾とサル、それぞれで運動方程式をたてるよ。質量が違うことに注意だよ。また、サルのほうの位置、速度、加速度は『'』をつけて銃弾と区別することにするよ。
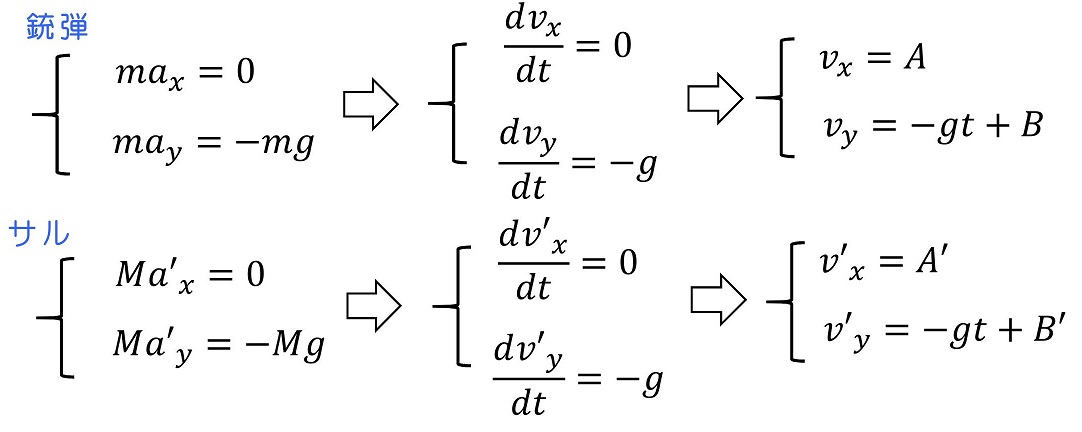
初期条件を考えるよ。銃弾の初速はθ方向にv0で発射され、サルは静止していたとしよう。
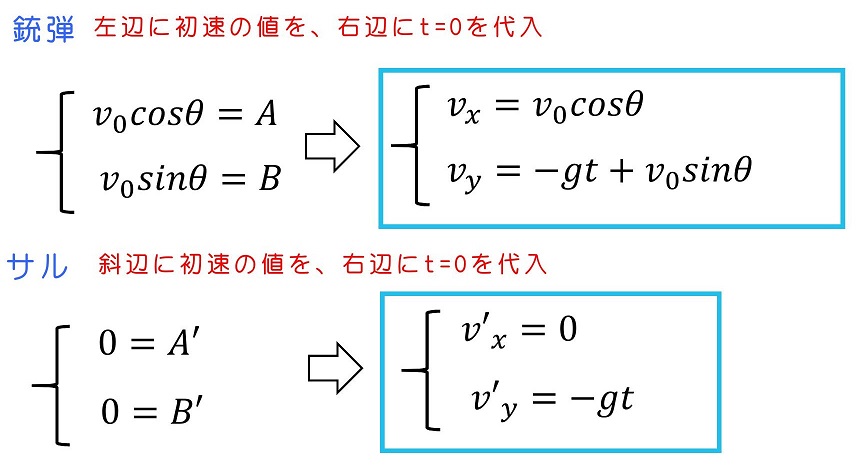
さらに位置座標の時間変化も求めよう。
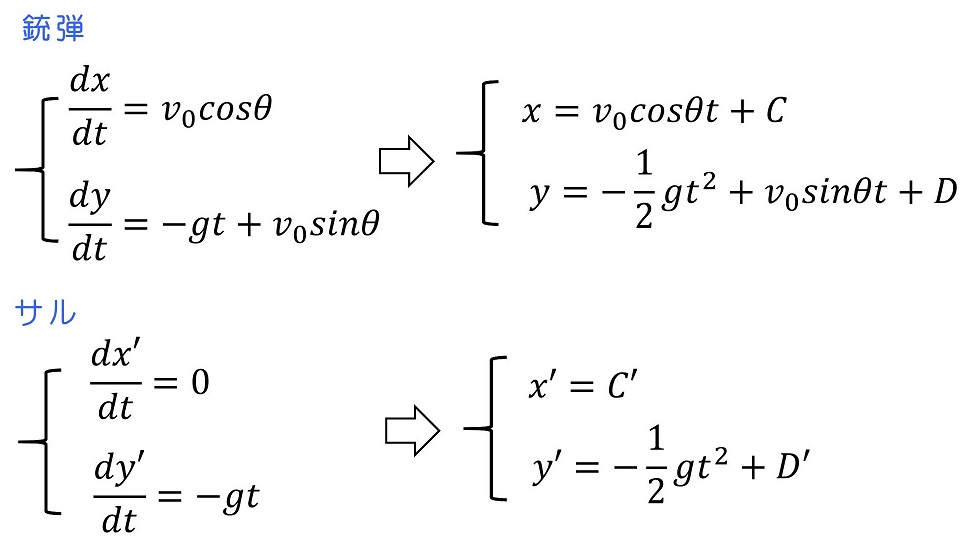
初期条件を考えるよ。銃弾の初期位置は(0,h)であり、サルの初期位置は(d,H)になるよ。
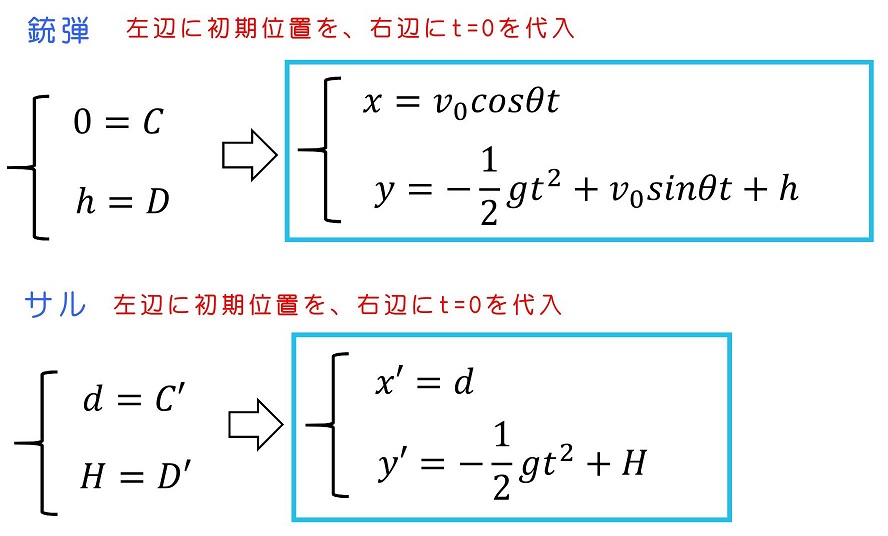
④運動を表す式を解釈しよう
銃弾がx=dに至るまでの時間を求めよう。銃弾の式を用いればよいね。

このときの銃弾とサルそれぞれのy座標を求めてみよう。
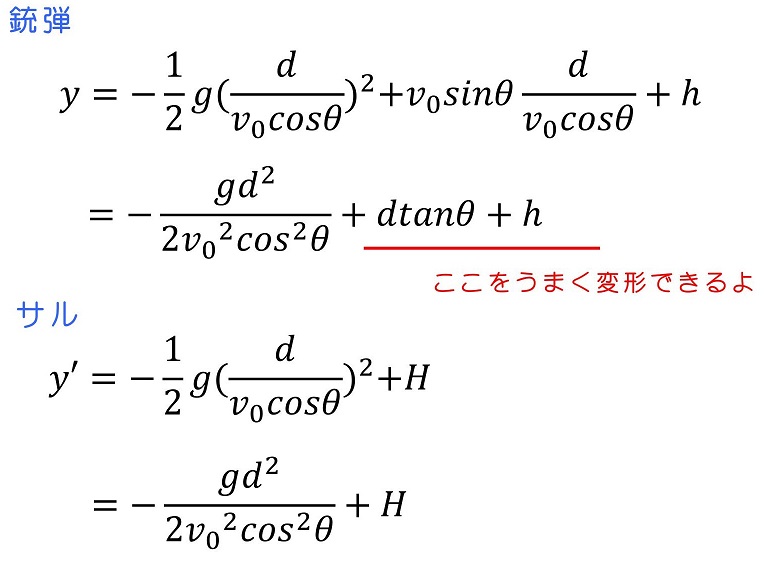
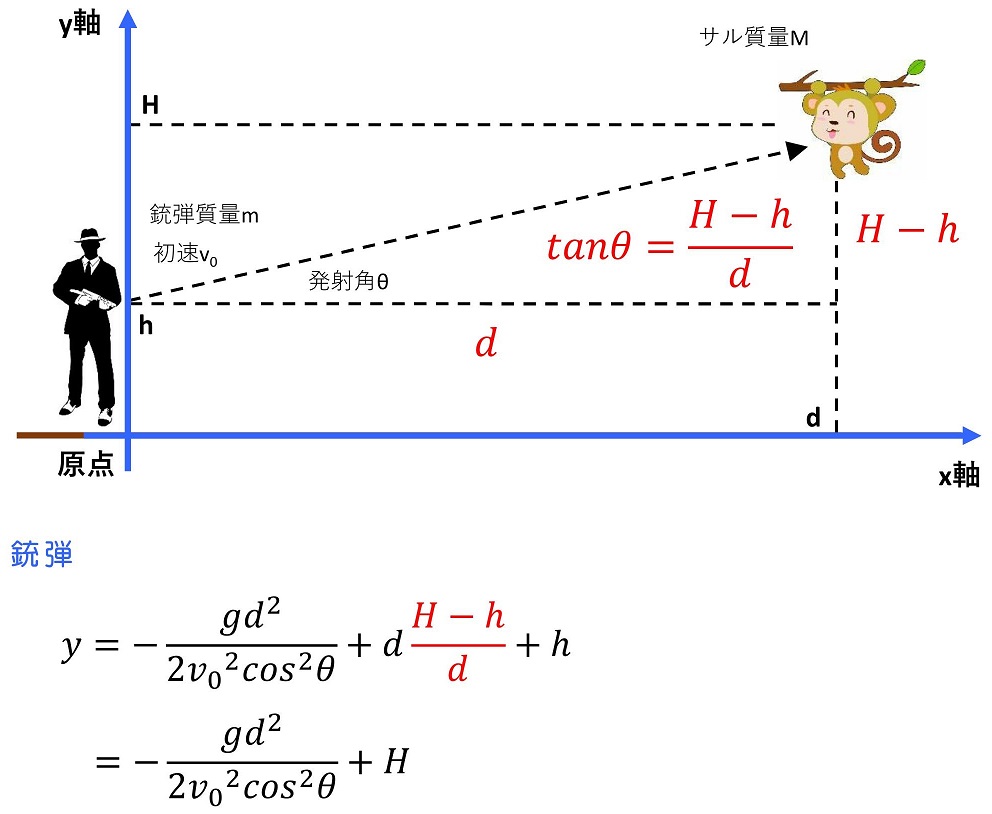
サルのy座標と、銃弾のy座標が一致したよね。つまり、銃弾はサルに『命中する』が正解になるわけだ。銃の狙いを定めるときはまっすぐサルをスコープで狙うわけだけど、実際には銃弾にも重力が働くからね、銃弾はわずかに下方向に引っ張られてしまうわけだ。サルが落下する分と、銃弾がまっすぐとんだ位置から下に引かれる分が一致するため、銃弾は当初の狙い通りサルに当たるわけだよ。つまり、もしサルが逃げようとして手を放さなかった時のほうが、狙いがそれることになるわけなんだね。