6.1 運動方程式を積分しようその2!(エネルギー保存の法則)
運動方程式を、単純に時間で積分することで、運動量保存の法則を導き出していたね。エネルギー保存の法則は、積分前に簡単な演算をしておくことで、導くぞ。運動方程式の両辺に速度vをかけて時間tで積分してみよう。<エネルギー保存>
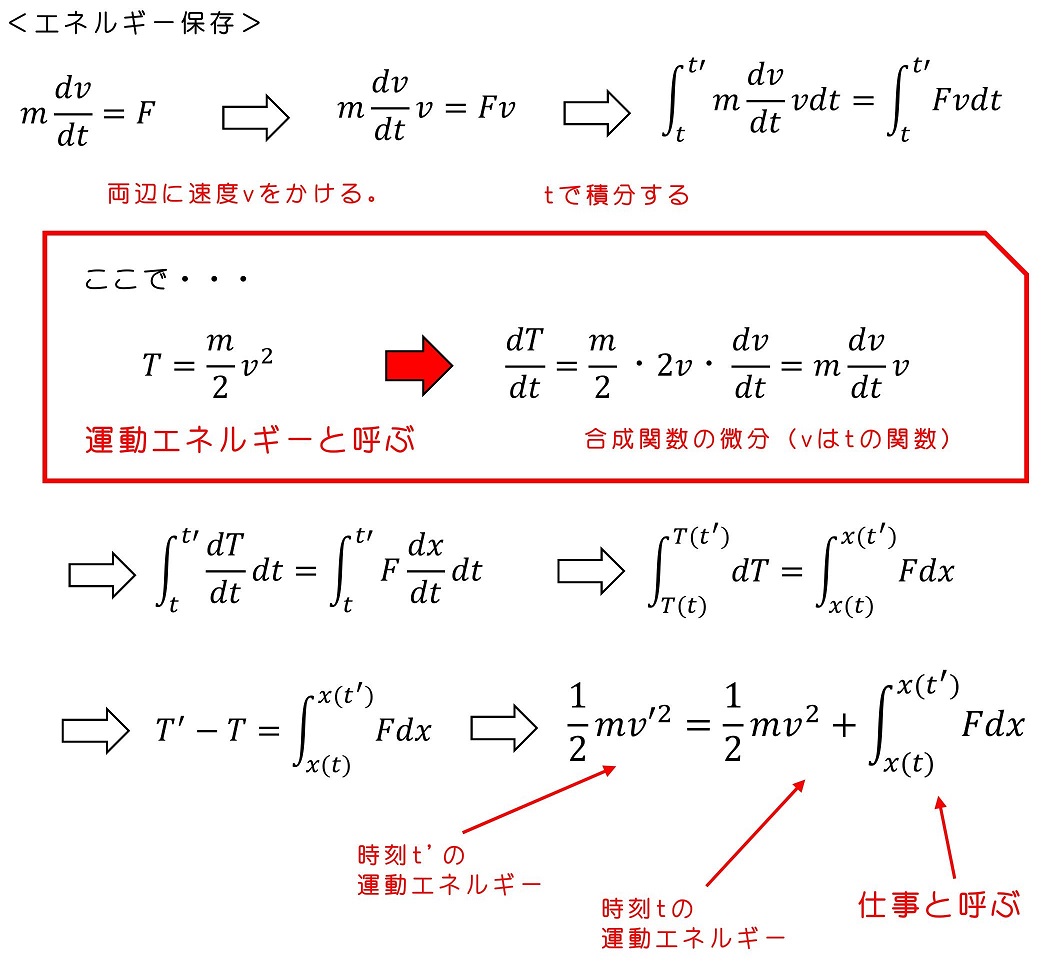
運動方程式を積分することで、新たな法則が得られたよ。時刻t'の運動エネルギーは、時刻tの運動エネルギーに仕事を加えた量だよ。

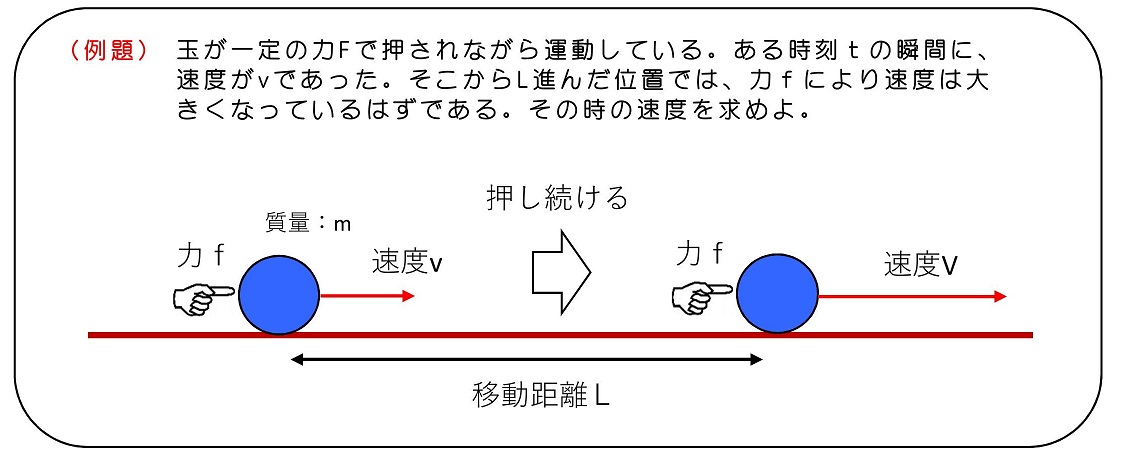
運動を予想する
一定の力で玉を押すと、加速度=f/mである等加速度運動になるはずだね。運動と同じ向きに力がかかっているため、玉は加速されて、最初は速度vであったとしても、だんだん速度は大きくなっていくよ。単位時間あたりに移動する距離がどんどん増えていくということだね。移動距離がLになった時の速度を求めよ、という問題だね。
軸を決める

玉が進む向きにx軸をとり、原点を速度vの時の玉の位置にしよう。求めたいのは、x座標がLの時の速度になるね。
式をたてて運動を解釈する
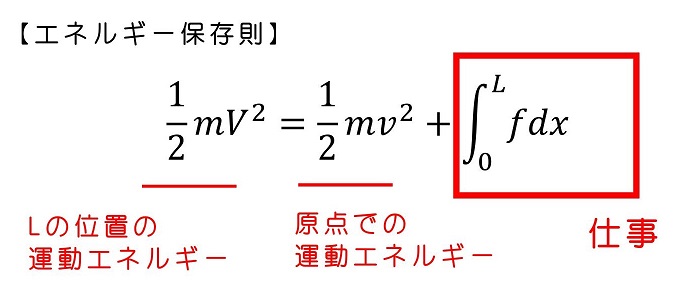
それぞれの位置での運動エネルギーを求めるのは難しくないだろうね。問題は、仕事を求めるときだ。

仕事と運動エネルギーより、式変形を行うことで移動後の速度が求まるよ。

仕事という名前がついている意味についても、少し言及しよう。『外力によって、玉は仕事された』という文脈で『仕事』という単語は使うんだよ。世間一般でいう、金銭を対価として要求する社会活動としての仕事とは異なり、物理での仕事とは、玉の運動エネルギーを増加させるような作用の大きさのことを言うよ。
6.2 3次元座標系でのエネルギー保存則
力が運動と同じ向きを持つ、1次元的な運動のエネルギー保存は知ることができたね。ただ、世の中には運動の向きと働く力の向きが不一致であることもよくあるよ。エネルギー保存則も3次元空間に拡張しておくと便利だよ。
1次元の時と何が違うの?と思うだろうね。1点、vを掛け算するわけだけど、ベクトルの内積という考え方を使ったところが異なるよ。
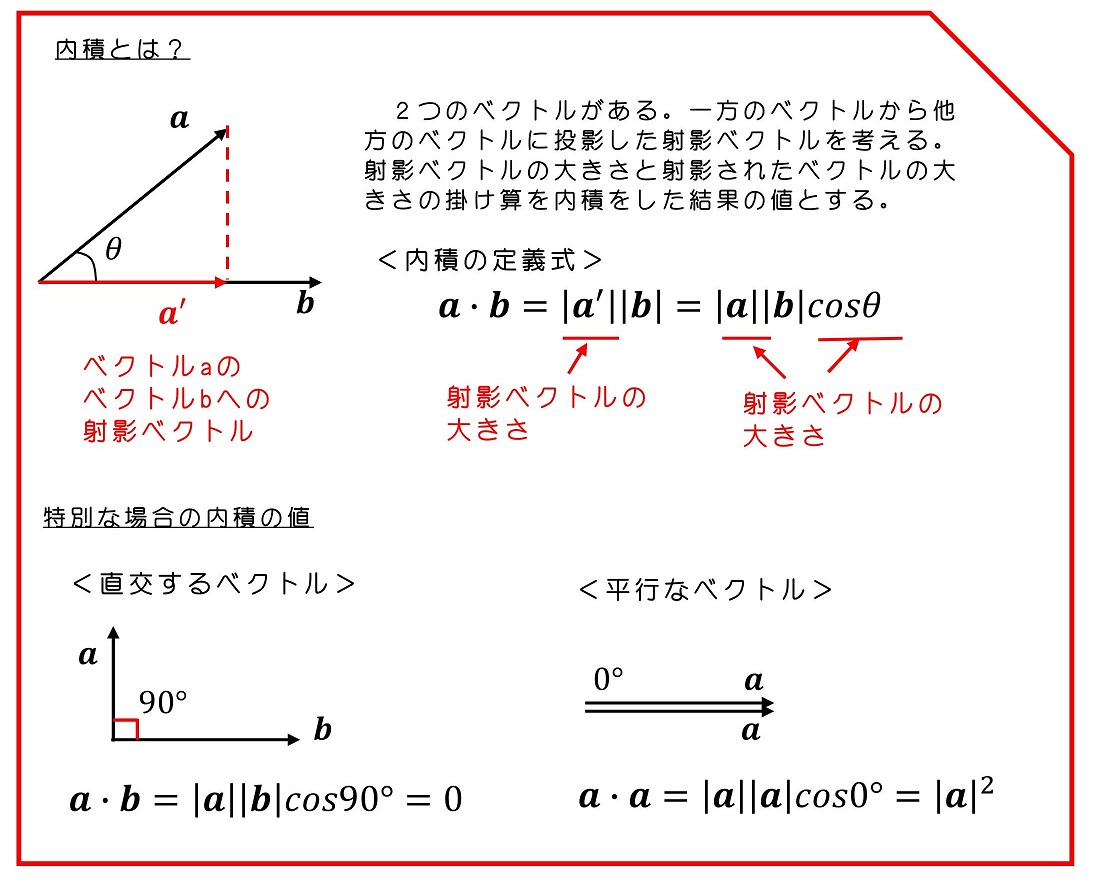
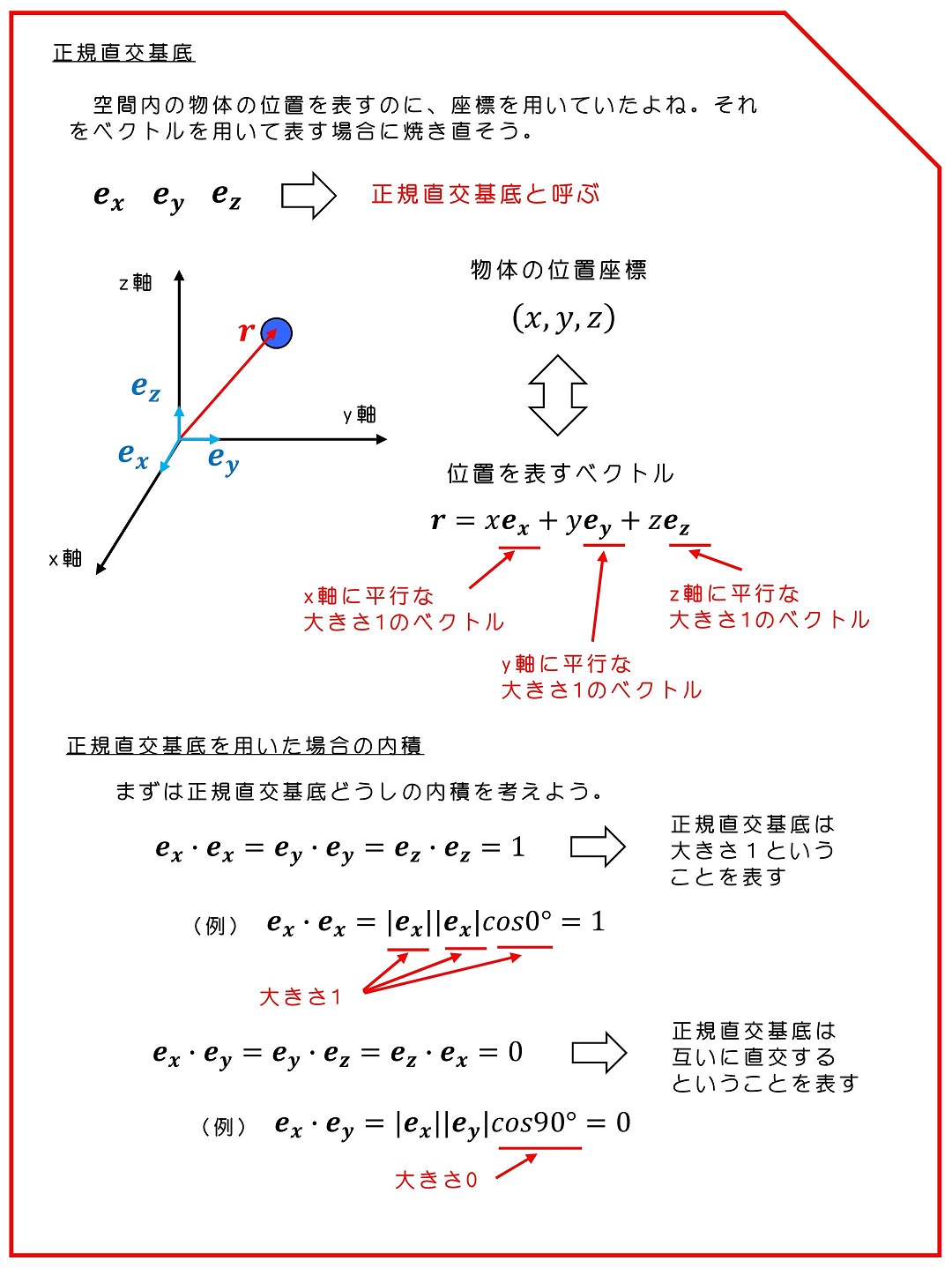
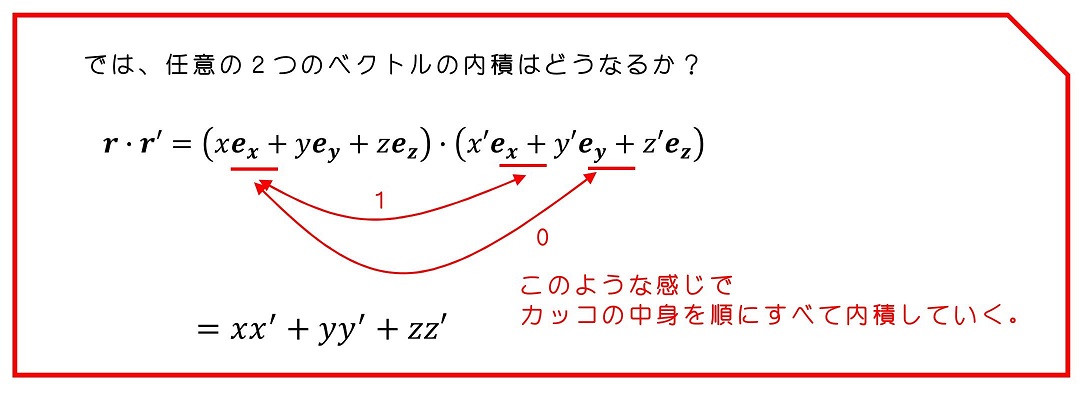
3次元座標系での運動エネルギーを次のように定義するよ。すると運動エネルギーの時間微分も求められるようになるよ。


1次元座標系でのエネルギー保存則と、同じような形式だね。運動エネルギーは先にも定義しているから、問題ないだろう?問題は、仕事の部分だね。例題を用いて考察を行おうか。
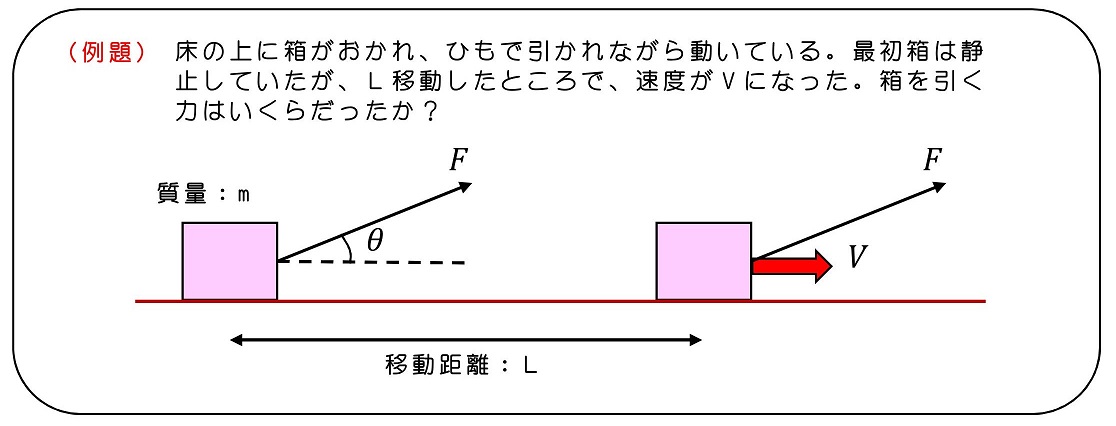
運動を予想しよう
力の向きが運動の方向と異なっているね。2次元的な運動と扱うのが良いよ。上下方向に運動は変わっていないため、力のつり合い関係にあるだろうね。一方横方向には加速しているよ。加速の原因となっているのは、斜め方向に引く力の横方向成分になるわけだ。
運動の軸を決めよう

式をたてて運動を理解しよう
エネルギー保存則を用いて運動を解釈しよう。
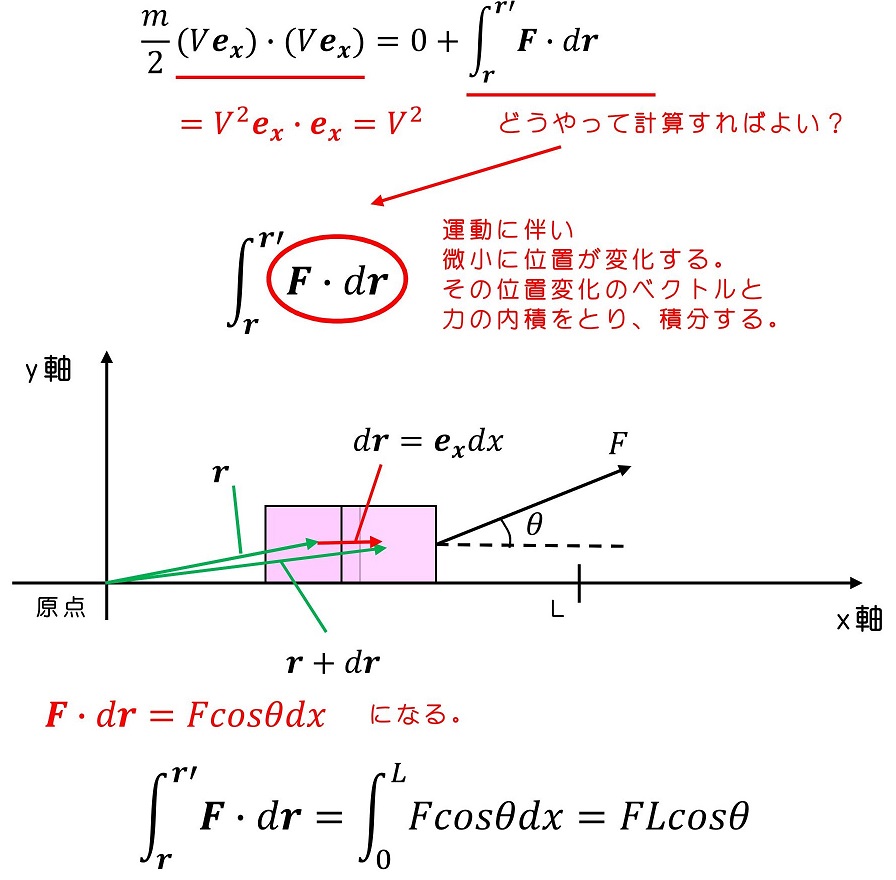

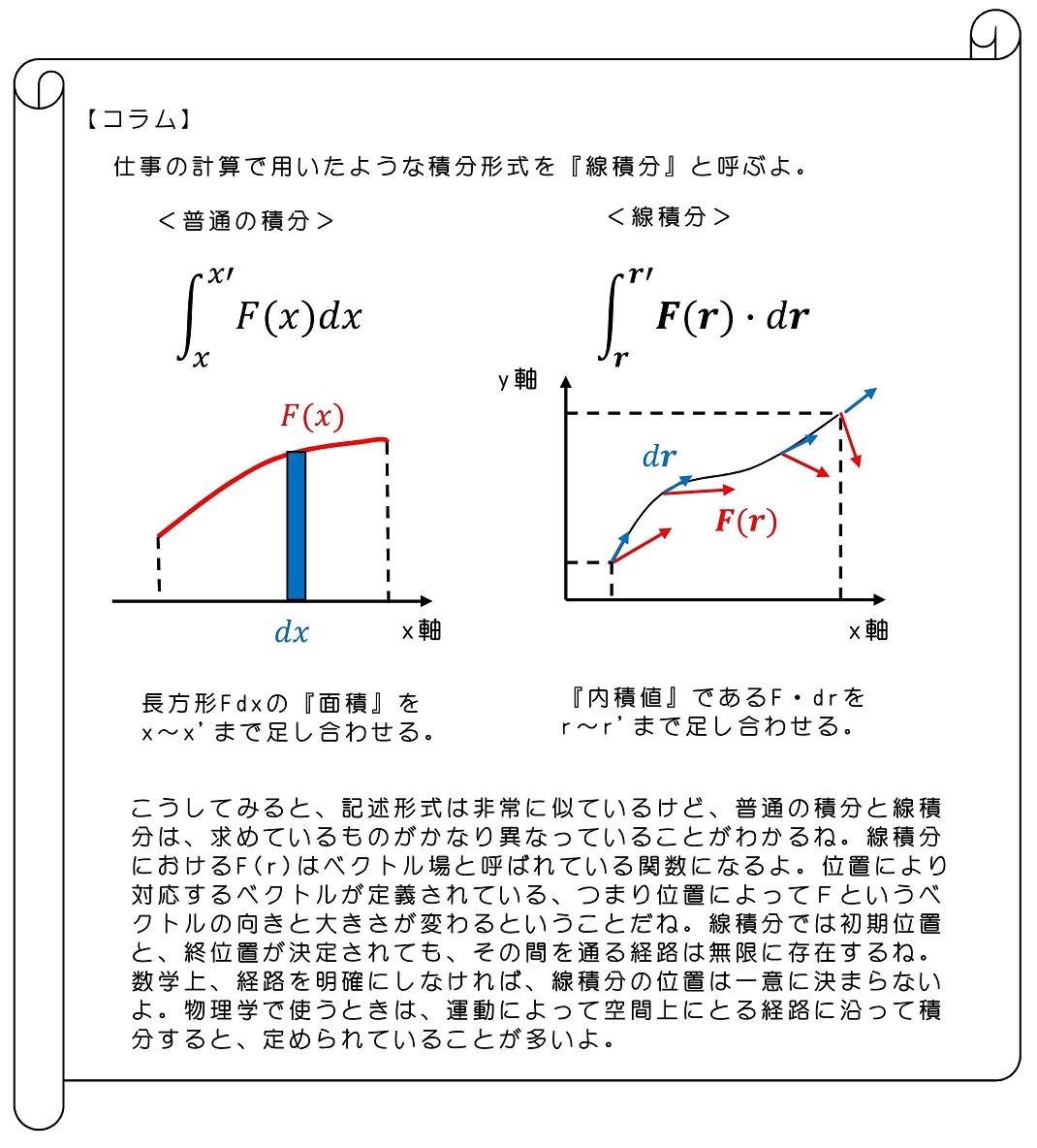
6.3 保存力による仕事
人間が仕事をすることで、運動エネルギーが増加する場合を考えてきたわけだけれど、自然界に存在するいろいろな力が仕事をすることによって、運動エネルギーが増加する場合もあるよ。自然界に存在するいくつかの力によついて議論していこう。まずは重力の場合だ。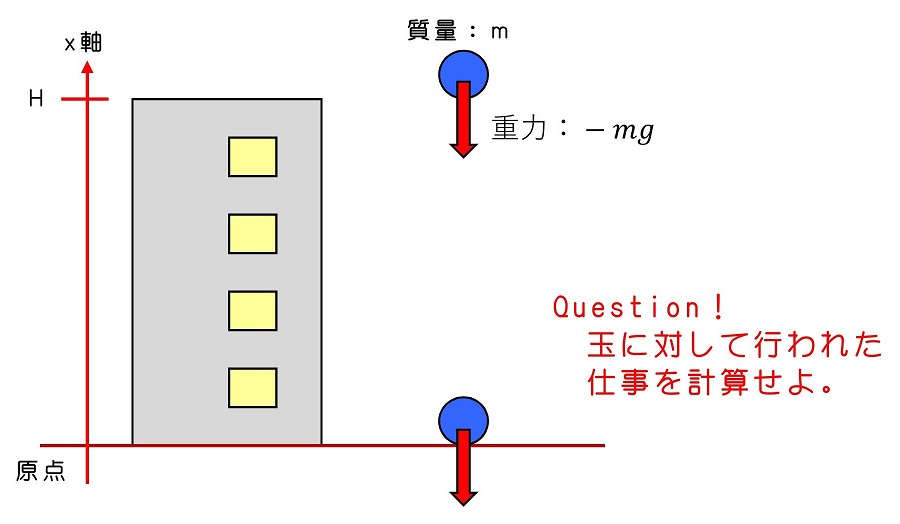
x軸を上向きにとって、ビルの頂上から地面に落下するまでの間の、重力が玉に対して行った仕事を計算しよう。運動の向きと力の向きが一致しており、1次元的な運動と考えることができるね。仕事も同様だ。

さて、似たような問題だが、もう一つ重力による仕事に関連して例題を考えておこう。
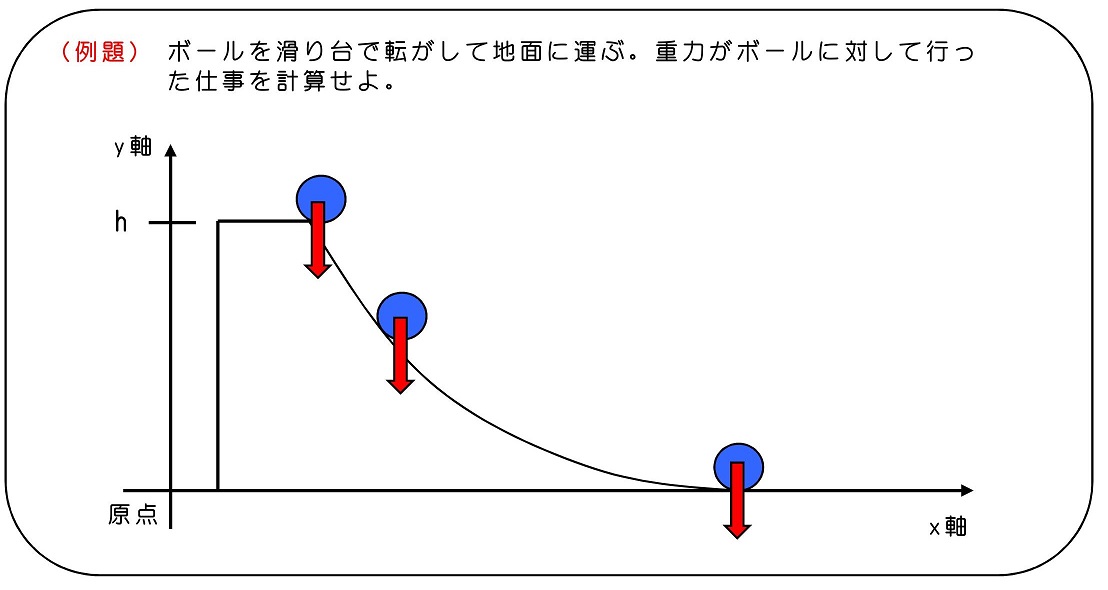
垂直落下と異なるのは、玉が滑り台に沿って、運動することだ。力の働く向きは常に下向きだが、運動は斜め下から横に、滑り台に沿って変化していくよ。2次元運動として、x軸とy軸を設定し、玉に対してなされる仕事を具体的に計算しよう。
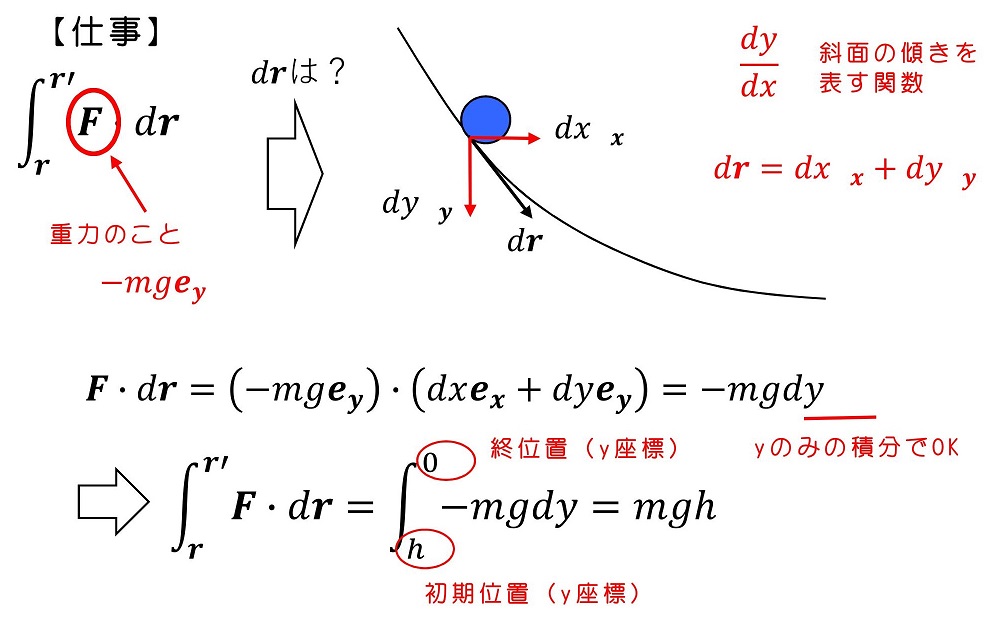
ここで、非常に重要な保存力という考え方を定義しよう。(重力は保存力の一つだ)今、斜面を転がるときの重力による仕事を計算したね。斜面の形状によって、この仕事の値は変わるだろうか?
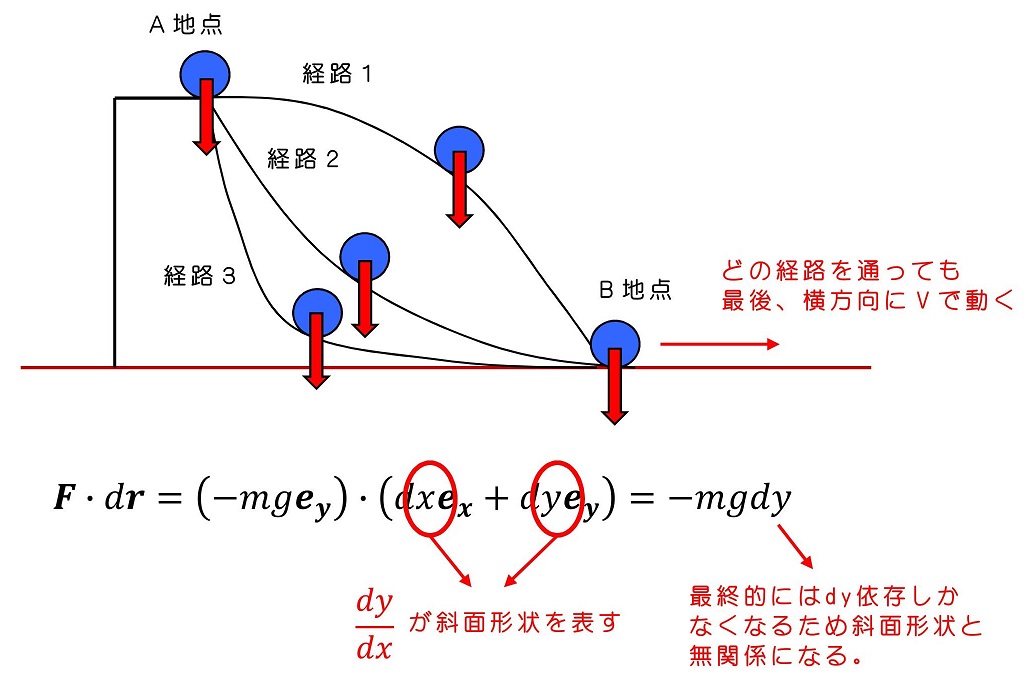
経路1~経路3いずれを進んだとしても、なされる仕事はmghになるよ。このため、B地点に到達したときに玉が持っている運動エネルギーはどのルートをとったとしても、同じになるよ。
このように、始点と終点が等しければ、経路によらず仕事が等しくなるような、自然界に存在する力のことを『保存力』と呼ぶよ。

6.5 重力による位置エネルギー
位置エネルギーという考え方を導こう。h1からh2に移動したときの仕事と運動エネルギーを考えよう。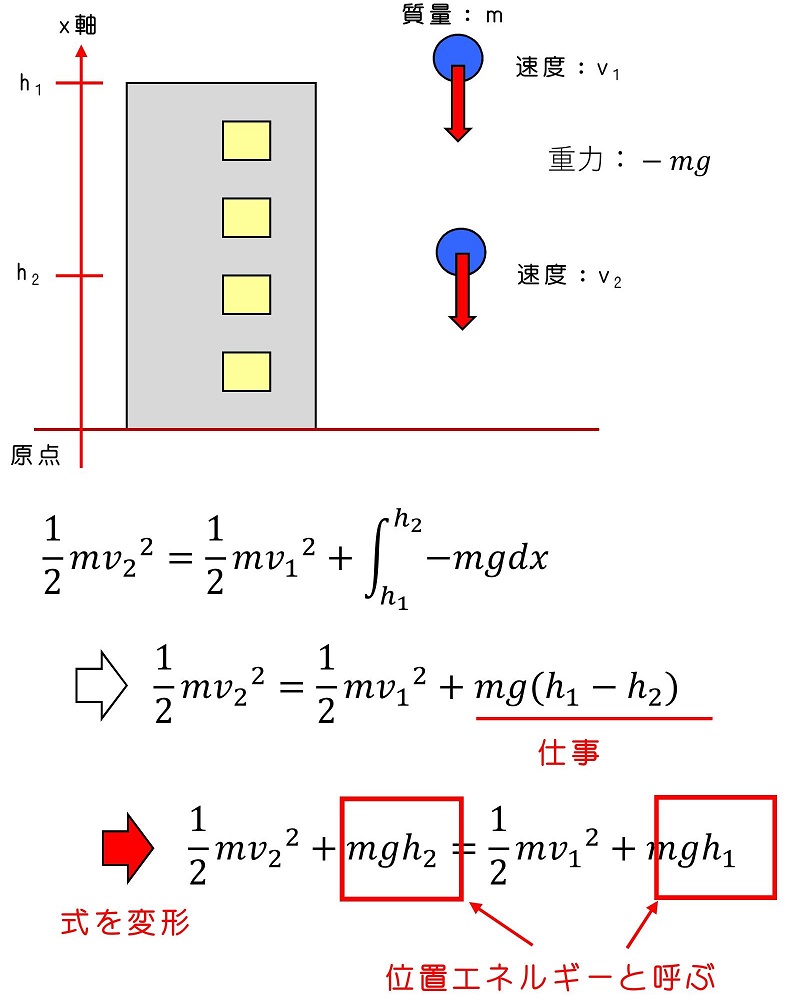
仕事という考え方と位置エネルギーという考え方は、似ているようで、『かなり』異なっているよ。そのあたりを少し議論しておこう。
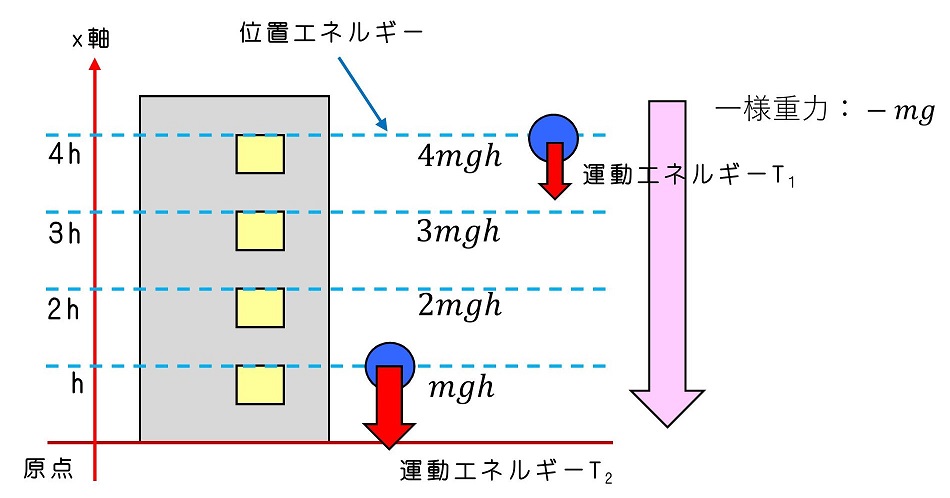
重力がなければ、物体は運動エネルギーしか持たないはずだよ。しかし、重力下に置かれることによって、エネルギーがかさ増しされるよ。物体のおかれる位置(高さ)によって、かさ増しされる量が決定されるため、このかさ増し分を『位置エネルギー』と呼ぶよ。
特に、重力は保存力であり、重力によってなされる仕事は運動の経路によらず、『高さにのみ』依存するね。働く力が保存力であるということは、高さが決定すれば、対応する位置エネルギーが一意に決まることを保証しているよ。また、位置エネルギーのことを物体がその場に存在するだけで、潜在的にエネルギーのかさ上げを受けるという意味で、『ポテンシャルエネルギー』とも呼ぶよ。

運動エネルギーと位置エネルギーの和を力学的エネルギーと呼び、運動において保存することから、特に力学的エネルギー保存の法則と呼ぶよ。
6.4 ばねの力による位置エネルギー
ばねをつなぐことによって、位置に依存した力が働くわけだね。ばねにつながれた物体の運動に対しても、位置エネルギーを導入するよ。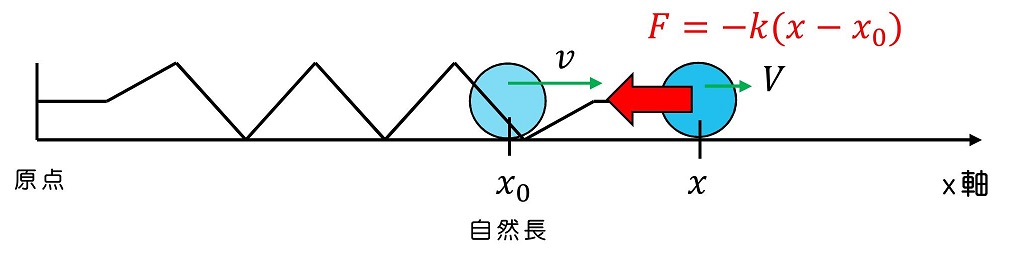
x0の位置に速度v右に動いていた。xまで動いたときの速度をVとする。運動エネルギーと仕事の関係を用いて式をたてる。

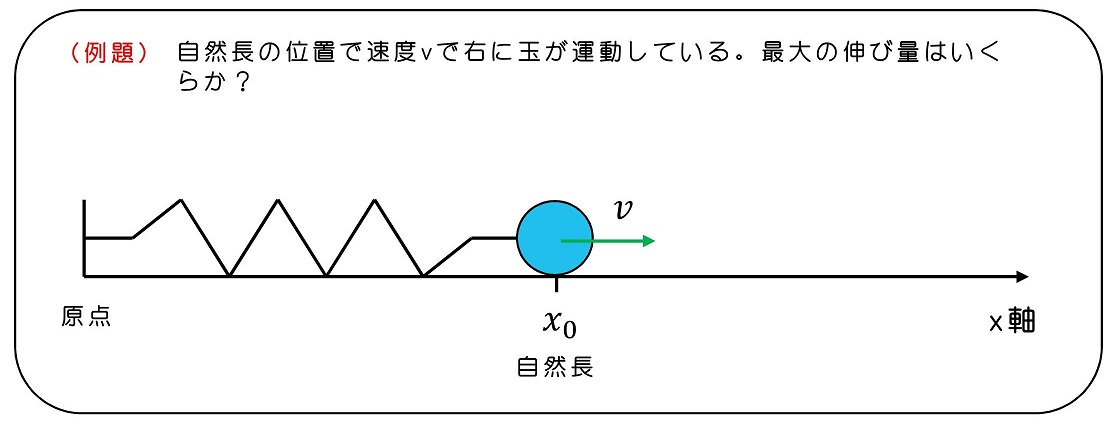
運動を推測する
自然長の時に右に動いていると、ばねを引き延ばしながらさらに右に動こうとする。ただし、ばねの伸び量が大きくなってくると、自然長に戻ろうとする力が強くなる。その結果、玉はどんどん減速されて、一定の箇所まで伸びたら、今度は向きを変えて左に戻ろうとする。最大伸びになっている瞬間は、速度がどんどん小さくなり、ゼロになった瞬間だ。
式を用いて運動を解釈する
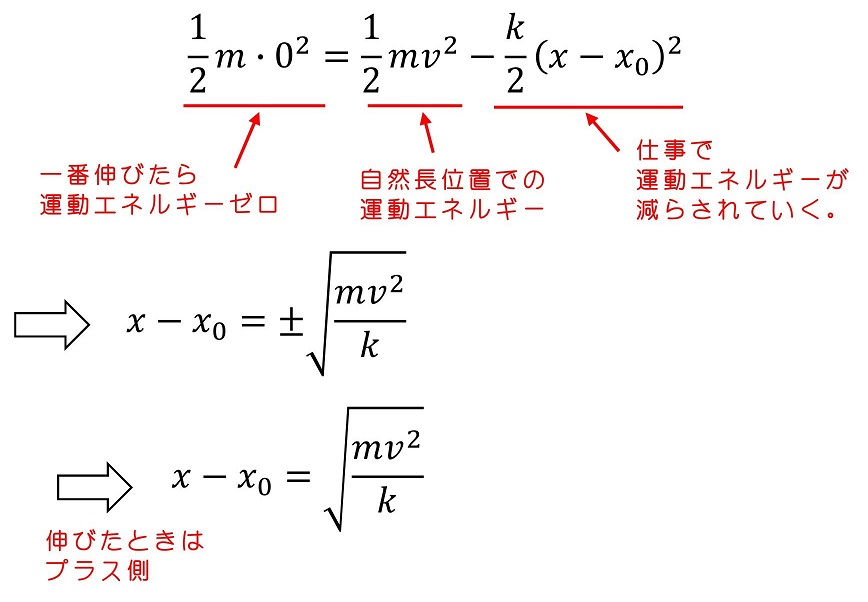
ばねの場合も、位置エネルギーを定義することができるよ。
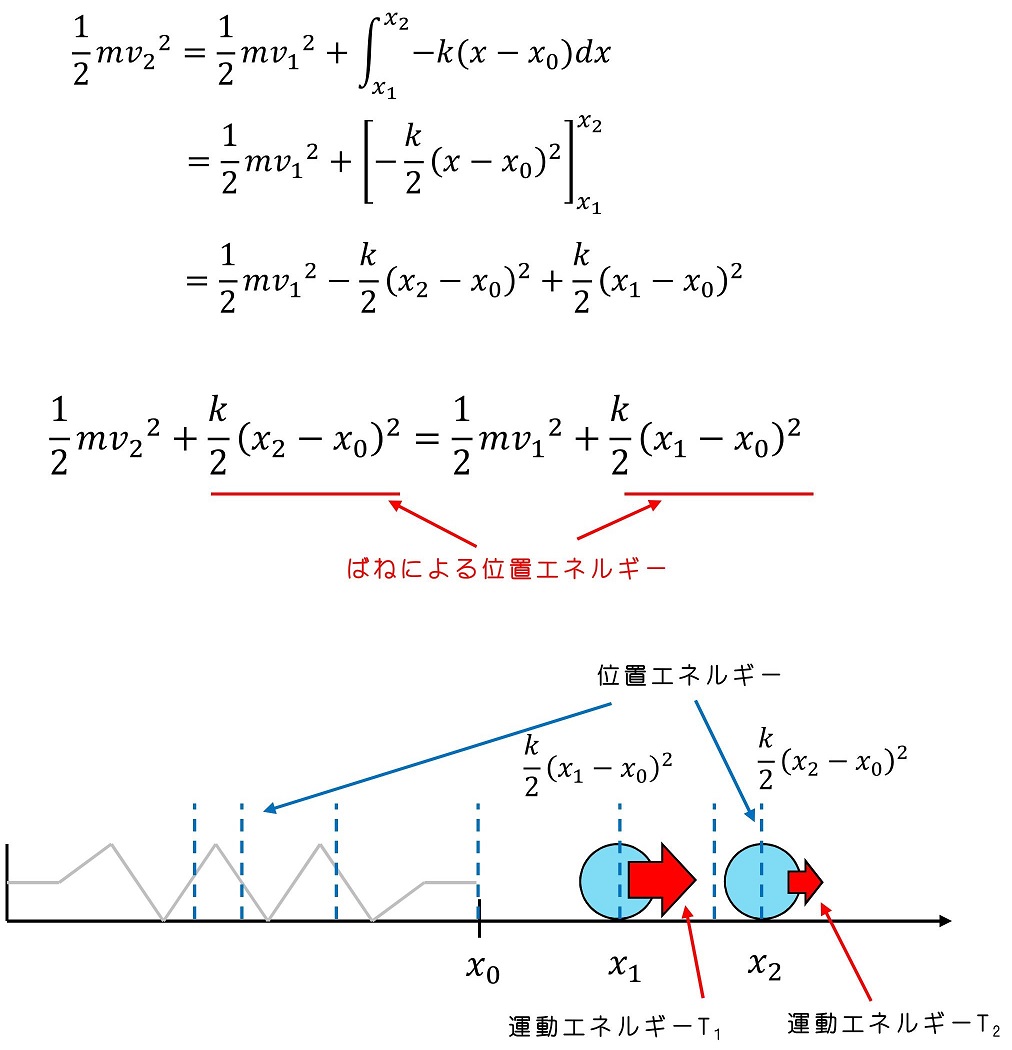
ばねにつながれていることで、位置によってエネルギーがかさ上げされるよ。伸びる方と縮むほうは、対照的にエネルギーがかさ上げされるよ。つまり、伸び量がΔxの時と縮み量がΔxの時の位置エネルギーは等しく1/2×k×Δxになるんだよ。