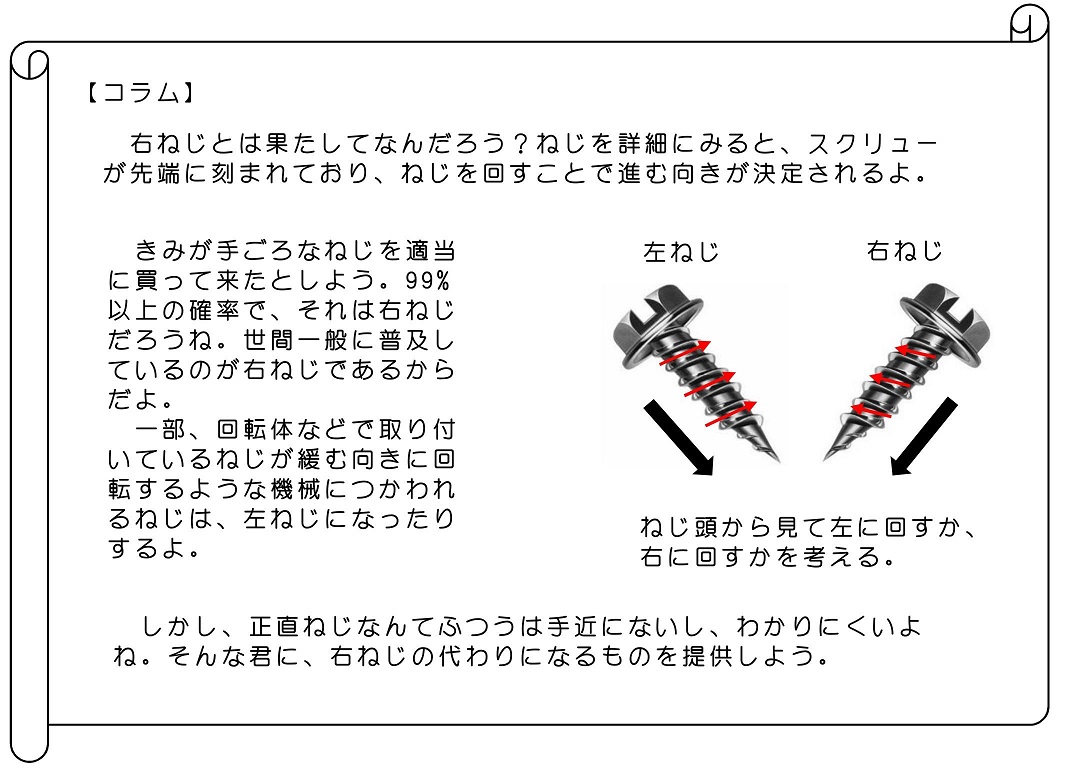
7.1 運動方程式を積分しようその3!(角運動量保存則)
最後の保存則について議論しよう。角運動量という物理量の保存則になるよ。まずは、角運動量について定義しよう。<角運動量を直感的に知ろう>
角運動量とは、物体の原点周りの『回転の向きと強さ』を表す量だよ。さて、回転の強さとは何だろう? 今、原点に『近い位置』を『ゆっくり』と『軽い』白玉が運動しているとするね。一方原点から『遠い位置』を『素早く』『重い』黒玉が動いているとするね。どちらの回転の強さがきついだろう?
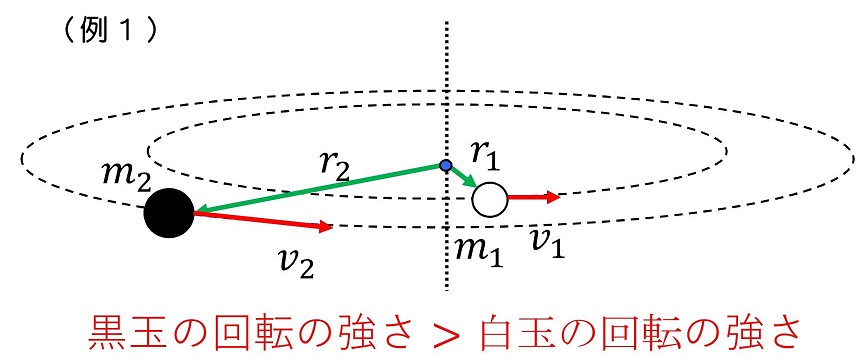
原点から『離れた位置』を『素早く』『重い』ものが動いているほど、回転の強さはきついと定めるよ。きみの直感と一致するかな?
回転の強さを表すのは難しい。原点からの距離や、速度の大きさ、質量だけで回転の強さは決定しない。例えば、下の例を考えてみよう。原点から物体までの距離が等しく、動く速度も等しく、質量も同じとしよう。異なるのは、原点に対して直角に移動するか否か、だね。どちらが原点周りの回転が強いと言えるだろう?
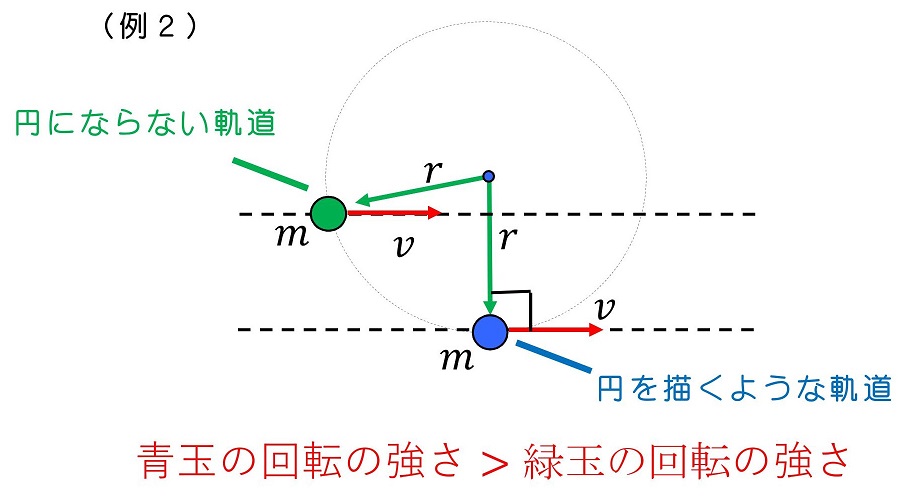
位置を表すベクトルと、速度を表すベクトルが直行している(青玉)場合に、原点周りの回転が強いと定めよう。直感と一致するかい?
さあ、回転の強さは、以上だ。次に回転の『向き』について考えよう。
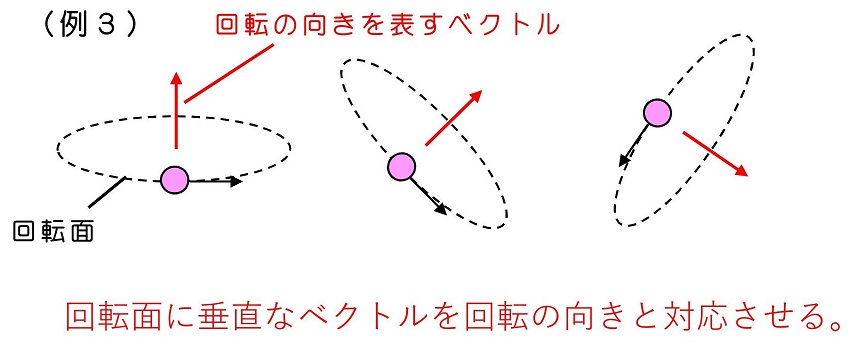
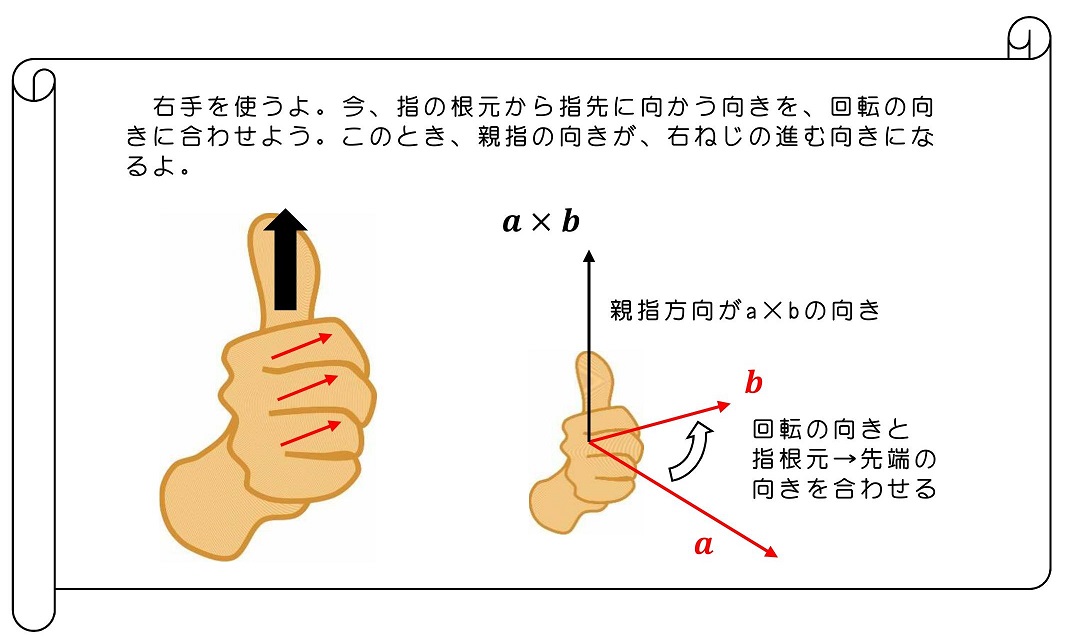
力学現象が発現するのは3次元空間だね。回転する向きも、3次元的にいろいろな向きをとりうるよ。回転の向きに対応させて、回転平面に垂直なベクトルを考えるよ。物体の実際に回転する方向と回転を表すベクトルの向きは『右ねじ』の回転とすすむ向きに対応させるよ。こうすると、任意の向きの3次元空間内の回転を表せるよ。

<角運動量を数学的に定義しよう>
運動量と比べ、角運動量は依存するパラメータが多く、式で表すのが難しそうだ。角運動量を表すのに最適な数学のアイデアがあるよ。ベクトルの外積という考え方だ。
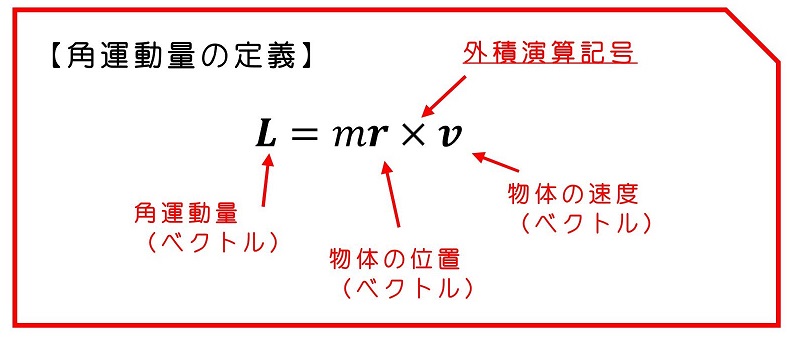
さて、外積の数学的な定義をここでは与えておこう。
<ベクトルの外積とは?>
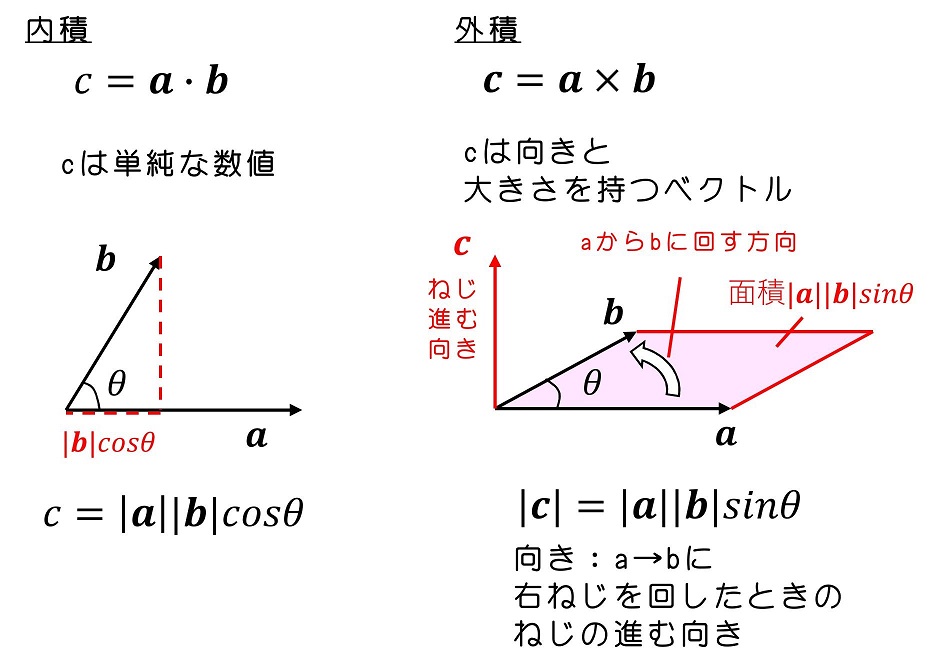
ベクトルの内積は、演算記号を「・」で表すが、外積は「×」で表す。内積は演算結果が「数」になるが、外積の演算結果は「ベクトル」になる。外積演算した結がどのようになるかを説明しよう。
<正規直交基底の外積>
座標とベクトルを対応させるために、正規直交基底を導入するよ。まず、正規直交基底同士の外積は何か知ろう。


<任意のベクトルの外積の成分表示>

外積の成分表示の計算結果は、サイクリックになるよ。
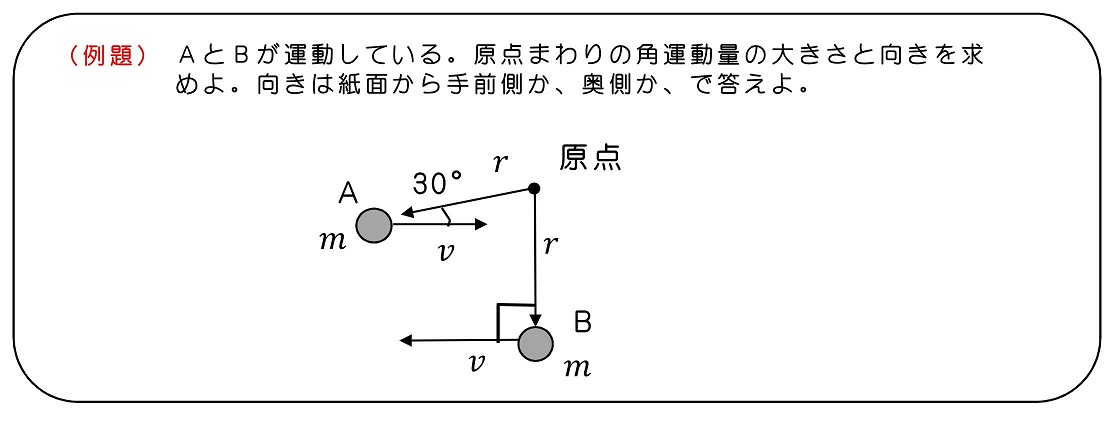

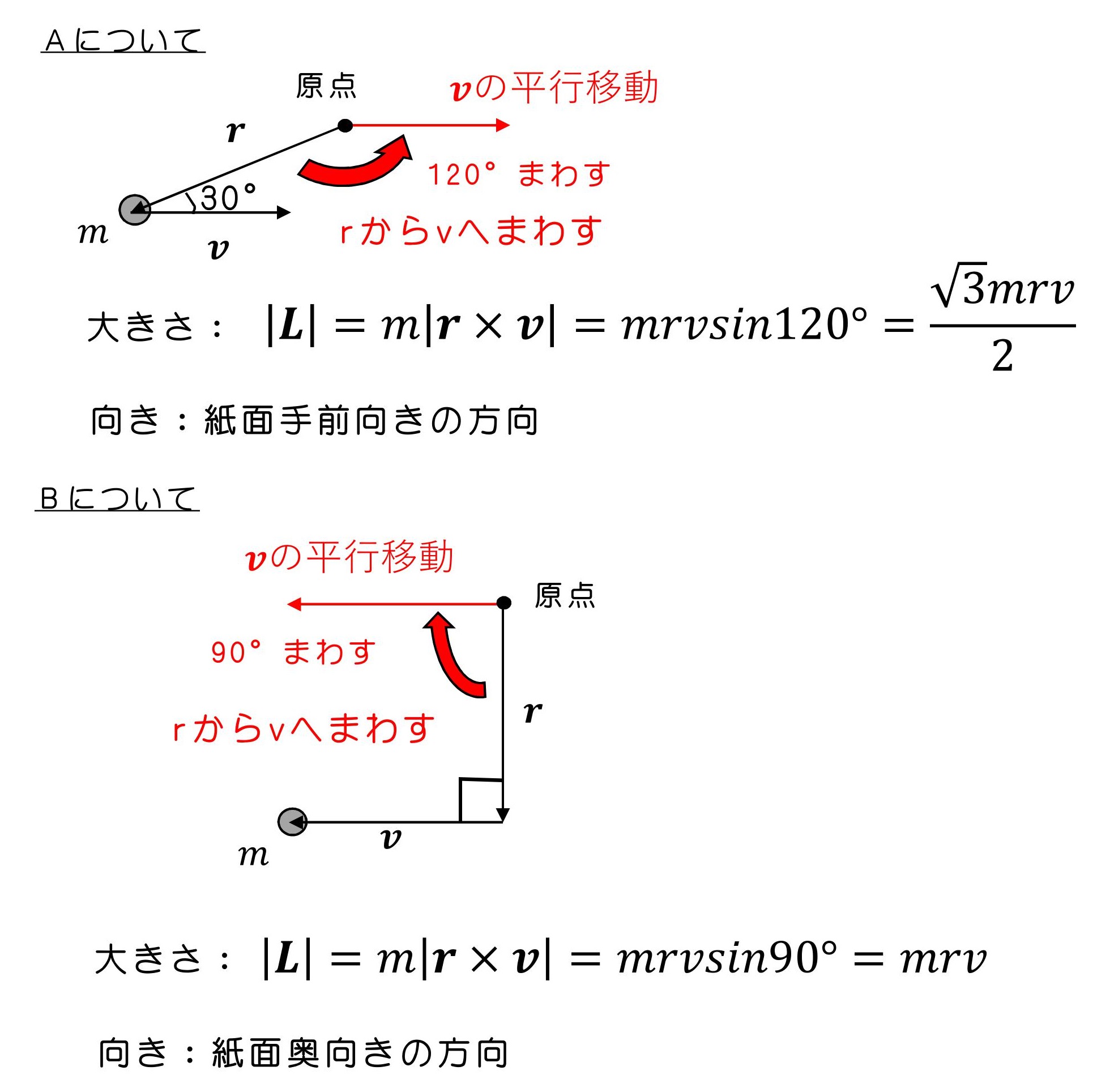
7.2 角運動量保存の法則を導こう
2体の物体があるとしよう。それらが、内力によってのみ力を及ぼしあっているとする。2体それぞれは、時々刻々の角運動量を持つわけだが、その足し合わさった量はどんな時間でも一定だ。これを、角運動量保存の法則と呼ぶよ。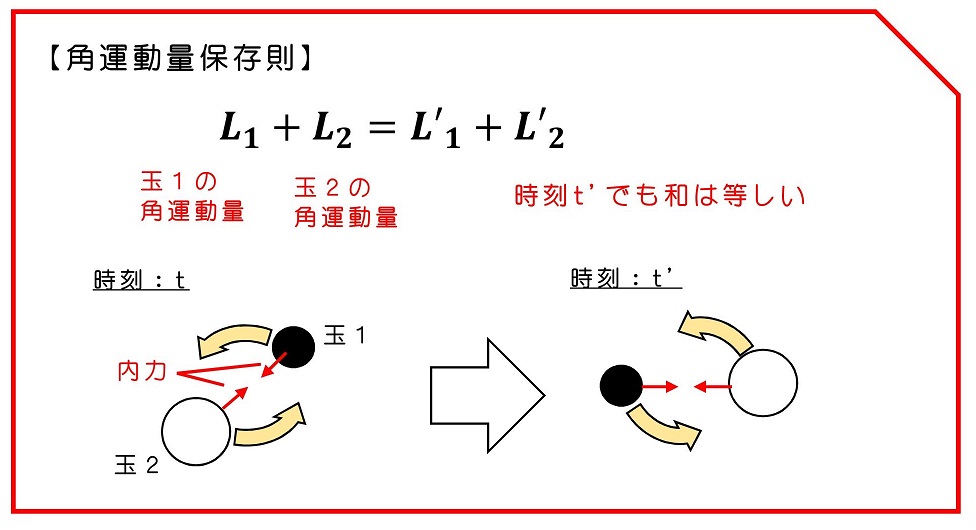
角運動量保存の法則は、運動方程式に所定の演算を行って、導くことができるよ。
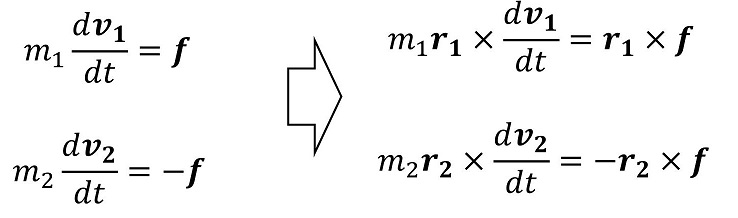
ここでいったん、角運動量の時間微分を導いておこう。
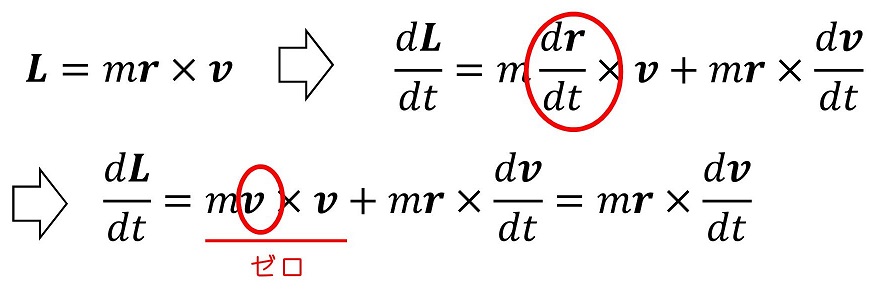
角運動量の微分を用いて、式を表そう。
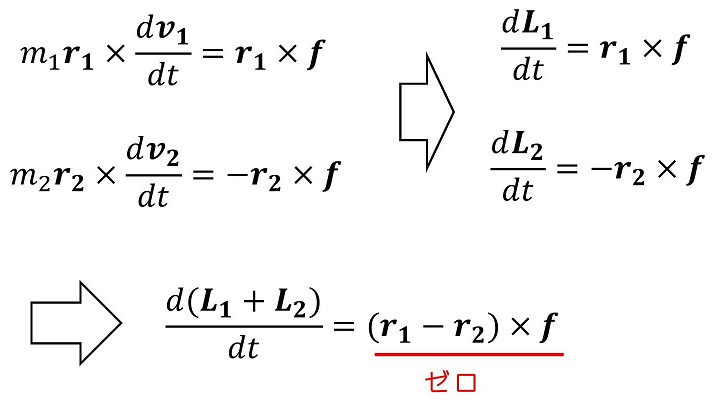
ここで、右辺がゼロになることが、物理的に導くことができるよ。
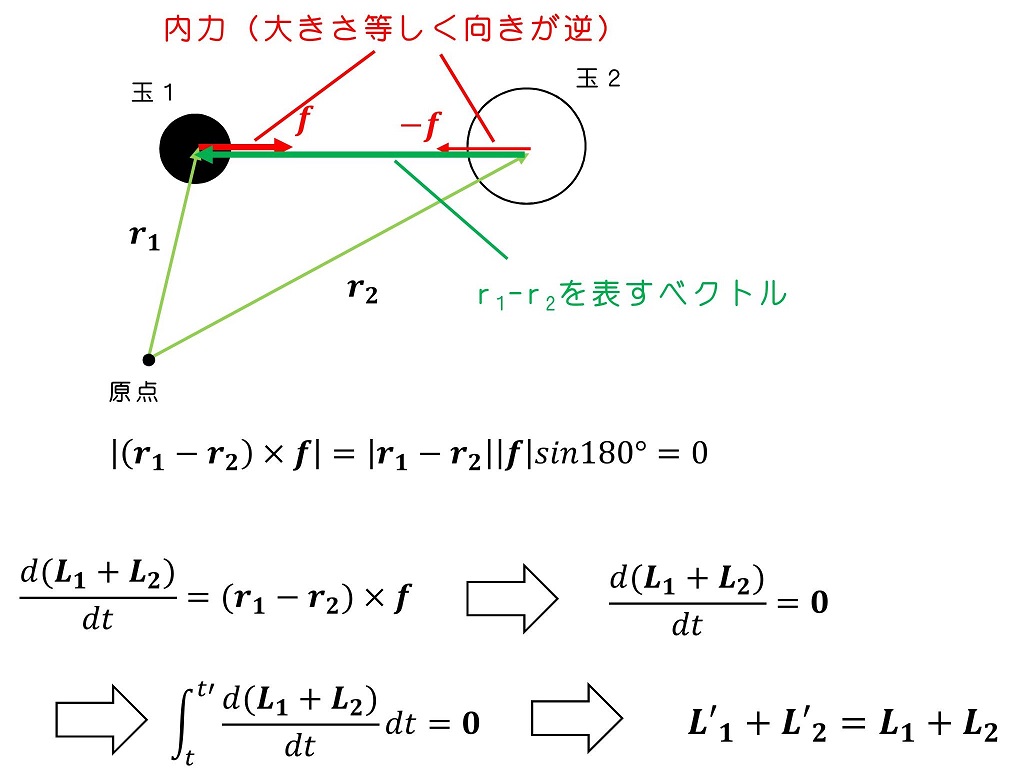
運動の様子を推測する
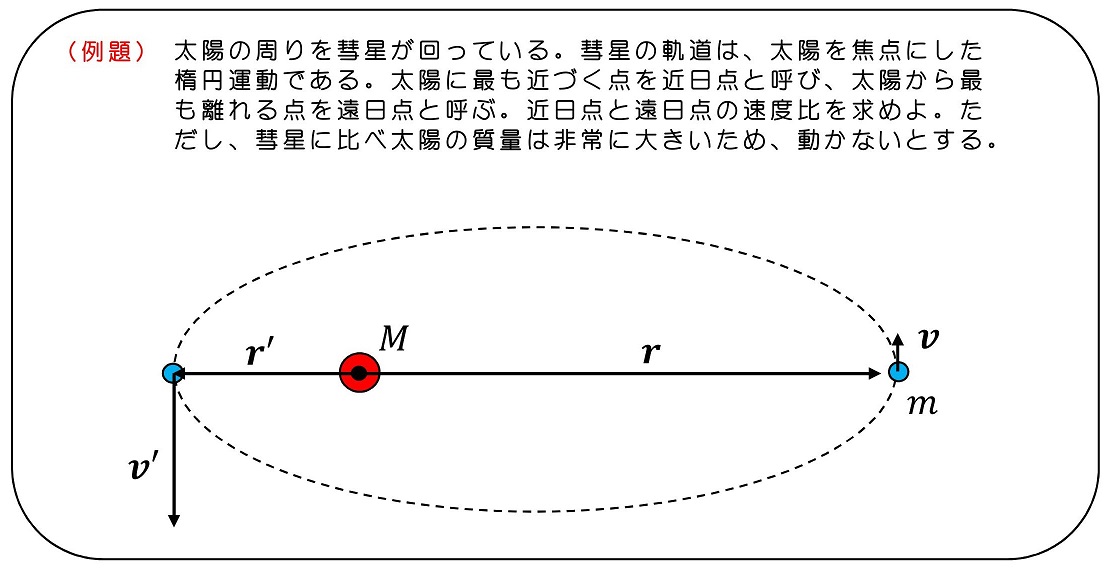
太陽がほとんど動かないと考えている。ある瞬間に太陽が原点位置にいたとすると、彗星との間に働く重力により位置が変わりうるが、太陽自身の質量が大きく、加速度が限りなく小さいため、太陽は彗星が運動している間、原点からほとんど位置変化しないと考える。
彗星の原点周りの角運動量を考える。近日点および遠日点では、位置ベクトルと速度ベクトルが直行している瞬間である。位置ベクトルから速度ベクトルの向きにねじを回すと、ねじは紙面手前側に進む。太陽は原点から動かない、つまり角運動量もゼロと考えるわけで、彗星の角運動量が保存すると考えるわけである。近日点は原点からの位置が近いので、角運動量が保存すると考えると、速度が遠日点に比べ大きくなるはずだ。
式をたてて解釈する
遠日点の瞬間を時刻tとし、近日点の瞬間を時刻t'として、角運動量保存の法則を用いる。

近日点の角運動量の大きさと、遠日点の角運動量の大きさを考える。