8.1 調和振動について
ばねにつながれた玉は、ばねによる復元力によって、きわめて調和のとれた振動運動を行うよ。ばね以外にも、長いひもにつながれた振り子なども調和のとれた振動を行うよ。これらを調和振動と呼び、いろいろな種類の振動の基礎をなすと同時に、波の挙動や量子力学の定式化にも一役かっているよ。非常に重要な概念であるため、細部の議論を行っていこう。調和振動とはなにか?
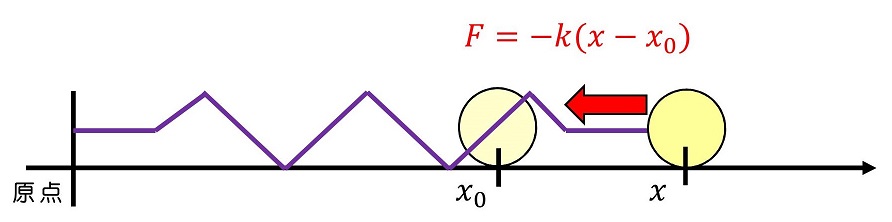
ばねに玉がつながれている場合において、運動方程式から運動を求めてみよう。

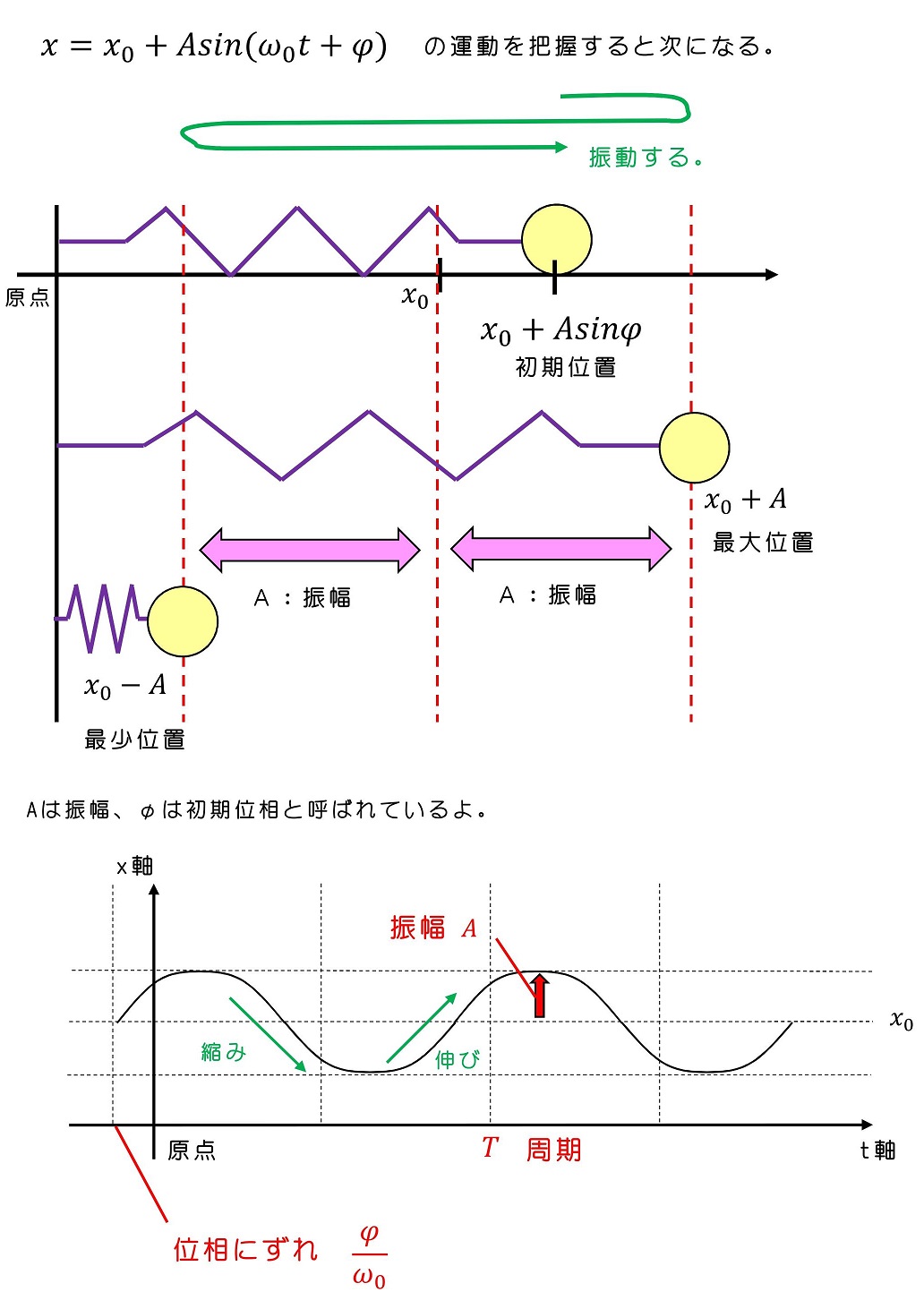
この解を理解するため、任意定数のうちA=x0/2、φ=0の場合を考えよう。
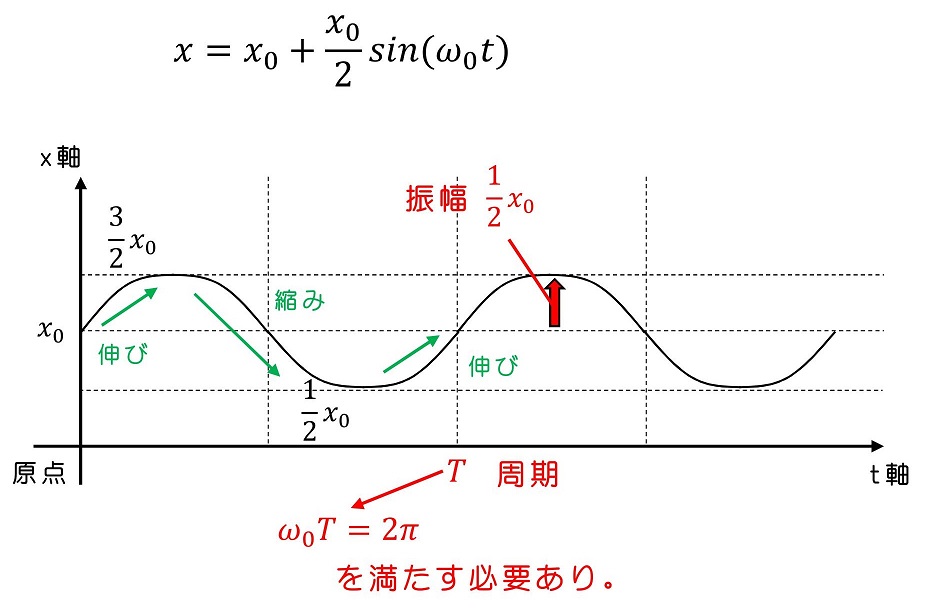
位置座標が時間とともに変位し、初期は自然長位置のx0にいたが、次に振幅x0/2で最大位置までばねは伸び、今度は逆向きに変位し最少位置までばねは縮み、最後にもとに戻る動きになるよ。元に戻るまでの時間を周期と呼ぶよ。
ω0は振動の周期と密接な関係があり、角振動数と呼ばれているよ。

これをベースにして、一般解の場合を考えよう。
あらわれてくる解が、純粋な正弦波という、非常に調和のとれた振動になっているよ。(通常自然界に存在するのはもっと複雑な振動だ)運動の解が正弦波のような波形になる場合を『調和振動』と呼ぶよ。
さて、方程式の解を天下り的に導入したわけだがこれを自ら求めることはできるだろうか?



8.2 空気抵抗がある場合のばね運動について
非調和振動の例をあげよう。まずは空気抵抗がある場合の運動についてだ。基本的に、ばね力によって往復運動をさせられるわけだが、抵抗により減衰させられて、最後は速度ゼロになって停止することが予想されるね。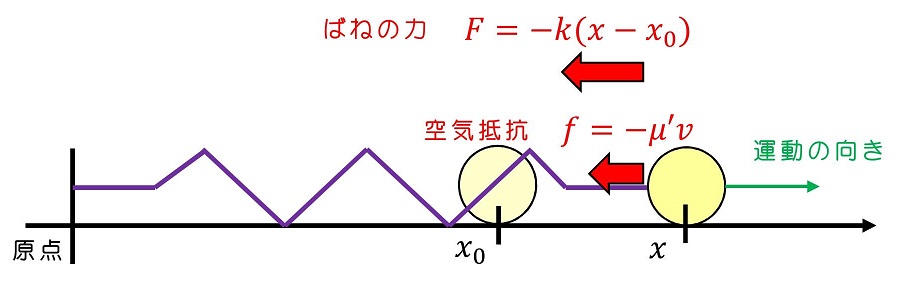
<運動方程式をたてよう>
空気による抵抗は、運動する物体の形状や材質によって非常に複雑に決定されるものだが、この問題としては単純に、速度に比例するとして扱おう。

<運動方程式を解こう>
解き方としては、8.1の時の調和振動の方程式と全く同じだ。

一般解を求めよう。
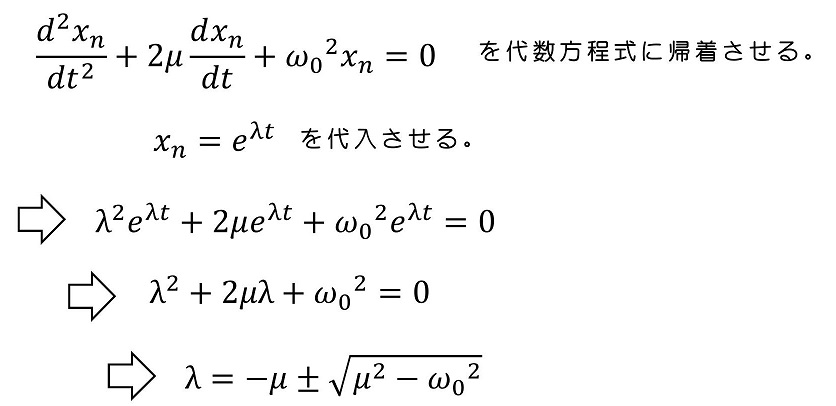
さあここで、2次方程式の解が①実数解になる場合 ②複素数解になる場合 ③重解になる場合で運動の様子が変わるよ。それぞれ詳細を把握していこう。
①実数解になる場合
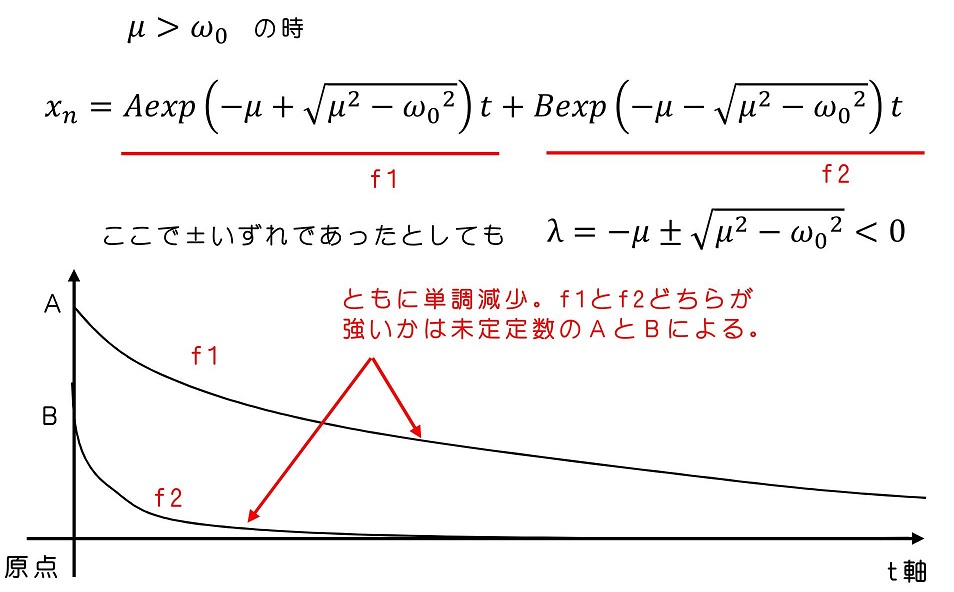
μが十分大きいとは、空気抵抗が十分に強いという意味である。ばねにつながれてはいるが、ばねの効果より空気抵抗が強いために、振動のモードに入ることなく、斉次解がゼロに減衰していくという意味である。(全体的な解としてはx0すなわち自然長に向かって減衰してゆく)
②複素数解になる場合
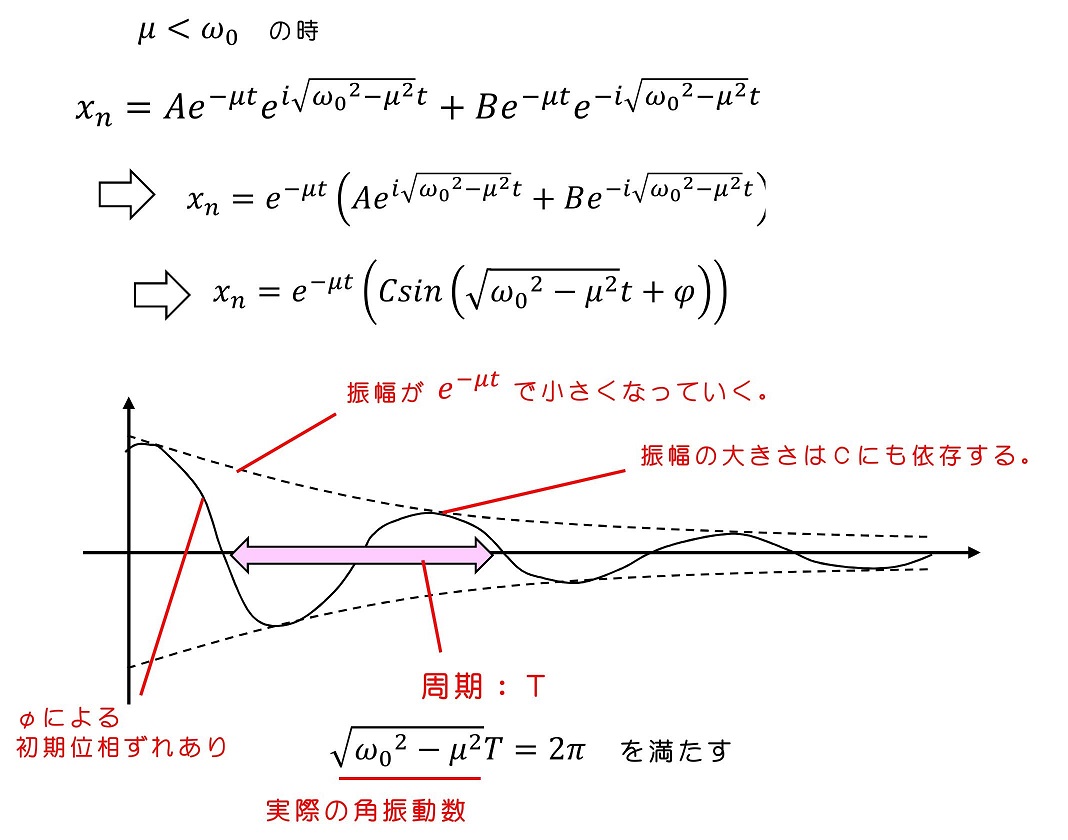
μが小さいと、ばねによる振動が強くなるよ。その結果、基本的には正弦波的に振動をするわけだが、抵抗もあるため徐々に減衰していくよ。抵抗が小さいほど、減衰速度は遅くなり、周期も調和振動に近くなっていくことが、式的にも理解できるね。
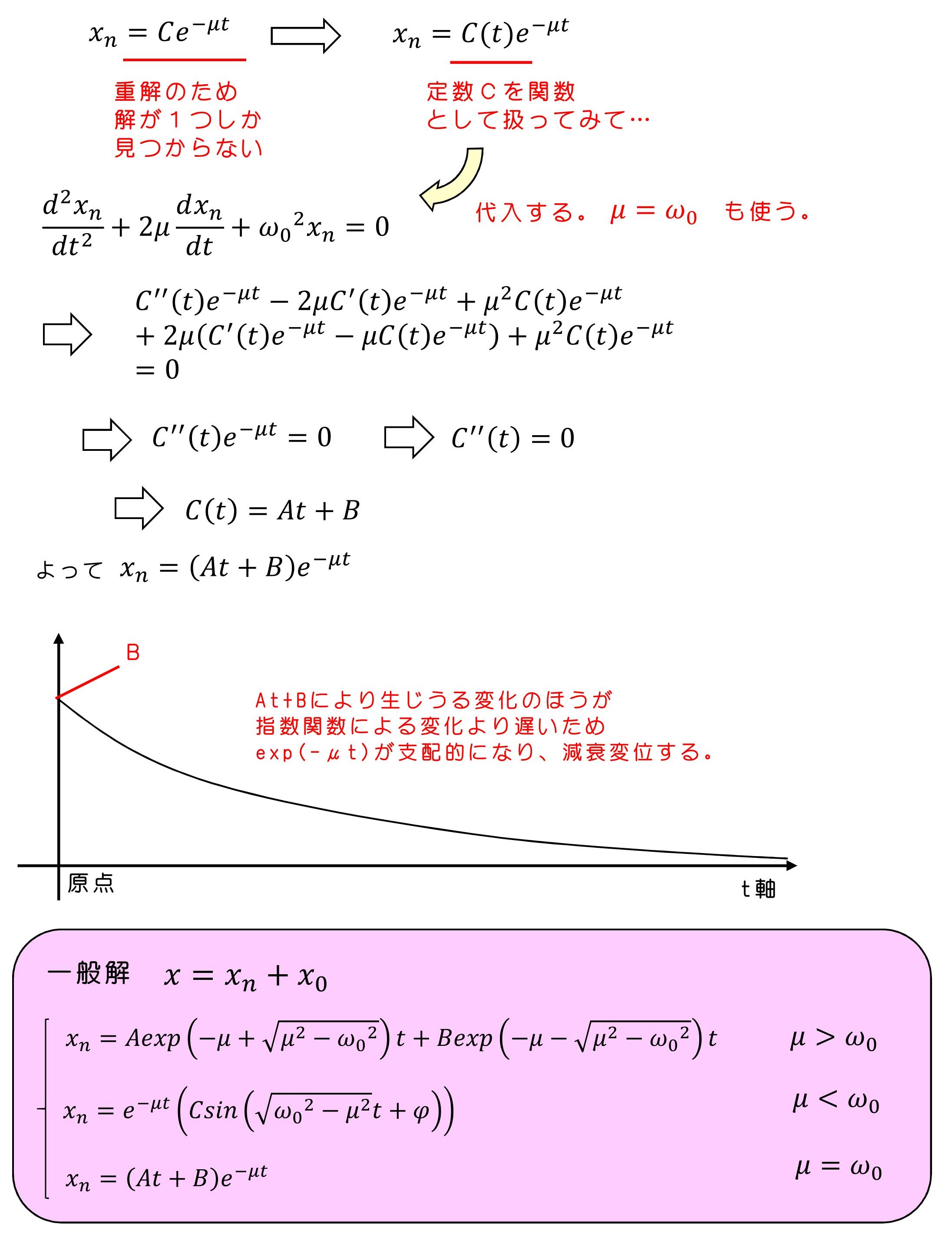
③重解になる場合
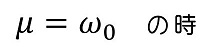
解が2個見つかり、その線形結合をすることで、未知数2個をもつ一般解を探していたわけだね。重解の場合、解が1つしか見つからないため、ストーリーから外れてしまうよ。さらに特別な処置が必要だ。
<定数変化法を用いる>
8.3 外部強制力のある振動について
外部から人間の力で強制的に振動を加えたときの運動について考えよう。加える力はFsinωtとするよ。また議論を単純化するために、ω0>μとしよう。また、自然長の位置を原点としよう。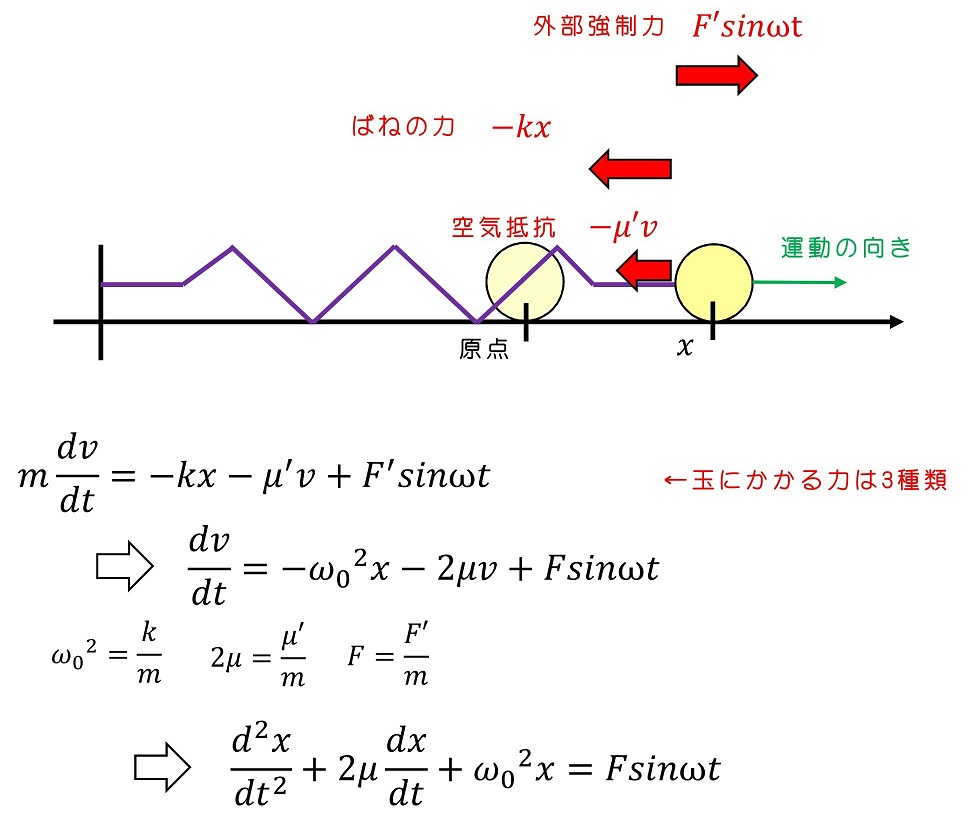
<運動方程式を解こう>
基本的に、解法は全く同じ考え方でよいよ。斉次方程式の解と特別な解の2つの和を考えればよいよ。斉次方程式の解は、強制力がない場合の解と全く同じだけれども、今回は特解を求めるのが非常に難しいね。

特解を求める前に、まずは斉次方程式の解をもう少し簡単にしておこう。
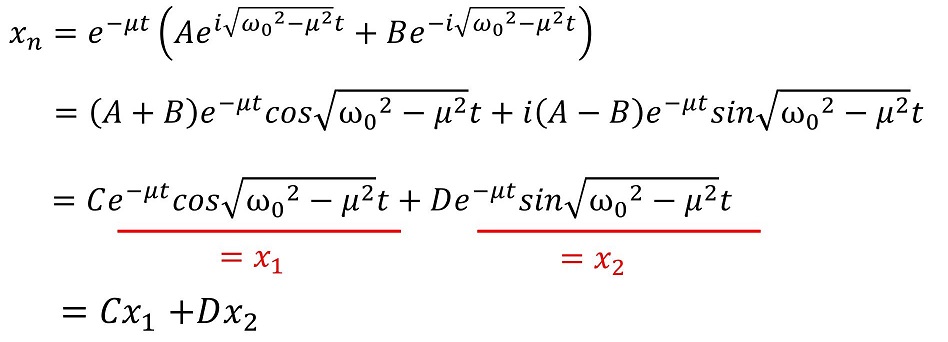
xnは必ず実数であるべきなので、CとDは実数、すなわちA+Bは実数であり、A-Bは虚数であることがわかるね。つまり、AとBは複素共役ということだ。さあ、ここをベースにして特解を求めよう。

さらに、2階微分も求めよう。
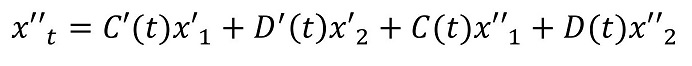
では、微分方程式に代入しよう。

さあ、2つの式が導出されたよ。今、x1とx2は既知であるため、CとDを求めるのが使命だったね。連立方程式を解けばよいよ。
<2式を行列で表示する>


両辺積分すれば、C(t)とD(t)が求まるよ。右辺積分する前に、簡単な積分を実行しておこう。


これで、C(t)とD(t)が求まったことになるね。今は適当な解を1つだけ求めればよいので、積分定数は無視しているよ。以上を総括して、一般解が求まるね。
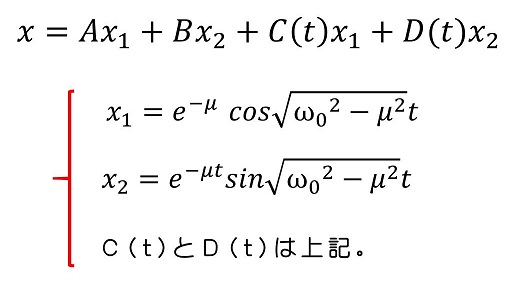
<解を解釈しよう>
本当に重要なのは、式変形で解を求めることではなくて、算出された解がどのような物理現象を表しうるか、を考察することだ。今、時間が十分長い時間経過した場合、どのような式の形になるかを把握してみよう。


さて、指数関数の部分は、x1やx2にある指数関数部とちょうどキャンセルされ、消えるね。そのため、無視可能だ。これにより、特解内にある関数はすべてサインやコサインになるため、減衰してゼロになることはない。
8.4 共振現象について
摩擦が十分に小さく、ゼロと考える。また外部から加える力の周波数がωに対して、これがばね定数と空気抵抗によって一意に決まるΩに限りなく近い値だと仮定する。この時、どのような現象が起こるか?8.4で求めた解から計算することができる。

外力の周波数が、系の持つ固有振動数(この場合ω0)と一致する場合、効率的に系にエネルギーを加えることができ、振幅は非常に大きくなる。このような現象を共振と呼ぶ。振動を取り扱う物理においては非常に重要な現象である。

8.5 2連振動について
二つの玉をばねで壁に固定したのちに、さらに二つの玉をばねで連結し、運動させよう。どのように運動するだろうか?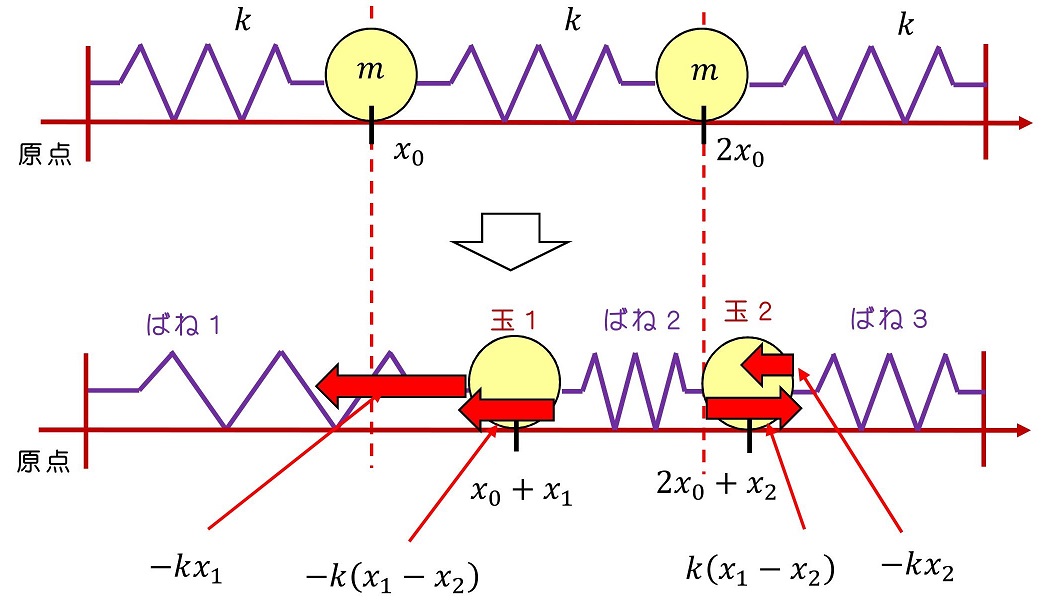
玉1の自然長からの変位量をx1、玉2をx2としよう。上の図は、x1>x2の場合に、玉にかかる力を示している。式にすれば、一般化されるためx1<x2も包括的に表すことができる。
運動方程式をたてて解こう

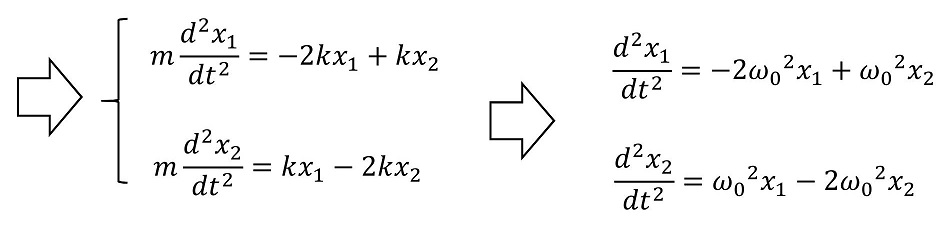
2階1次の連立微分方程式だ。この方程式を、最終的には調和振動に結び付けられる方法を利用して解こう。
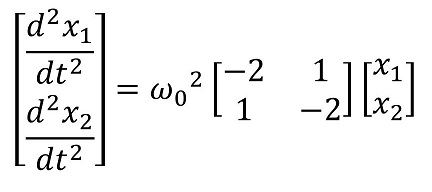
今ここで、行列の対角化を利用しよう。行列の対角化に必要な考え方として、固有値と固有ベクトルという考え方が存在するよ。
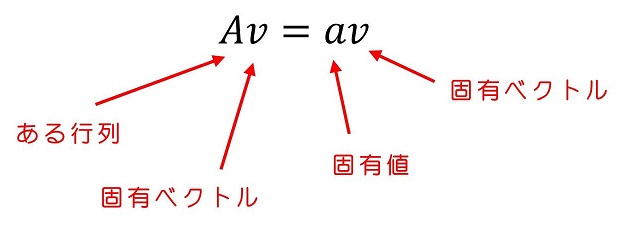
【固有値、固有ベクトル、対角化】
ある行列Aが与えられる。Aの種類によっては、Aに対応したベクトルとある値が存在する。このベクトルvとある値aは、Aにvを作用させると、vのa倍になるという条件を満たす。vをAの固有ベクトル、aをAの固有値と呼ぶ。
具体例でみてみよう。

注意すべきは、当然、すべてのベクトルが固有ベクトルになりうるわけではないことだ。

今は天下り的にベクトルを与えたら、それがたまたま固有ベクトルであり、固有値も求めることができた。固有ベクトルと固有値を直接求めるにはどうすればよいか?
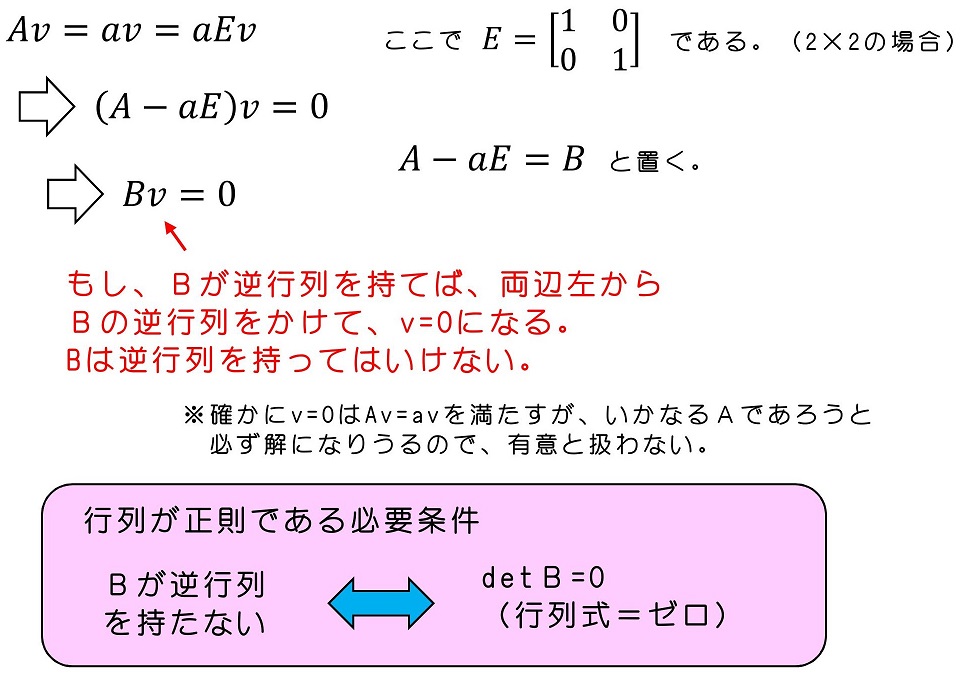
行列式=0という条件から、固有値aがすべて求まる。それをベースにして対応するベクトルを探してゆけばよい。ここから先は例があったほうが良いから、そちらで示そう。

固有ベクトルを用いて行列の対角化を行うことができる。
対角化とは?
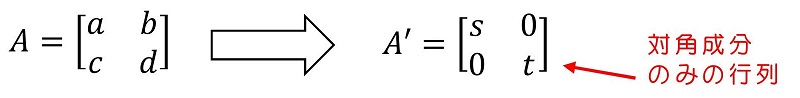
Aに特定の演算をすることでA'に変形すること。
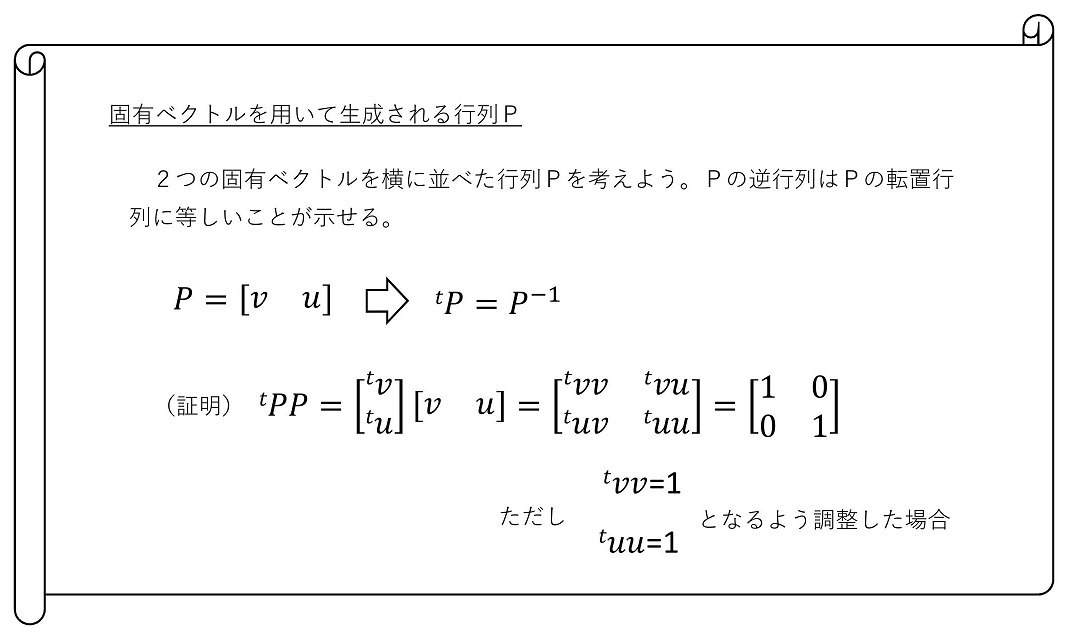
対角化とは、行列の斜め成分以外をゼロにする操作のことだ。対角化は所定の行列で両側から挟む演算をすることで、行うことができる。どのような行列で挟めばよいか?固有ベクトルを用いて作成された行列だ!
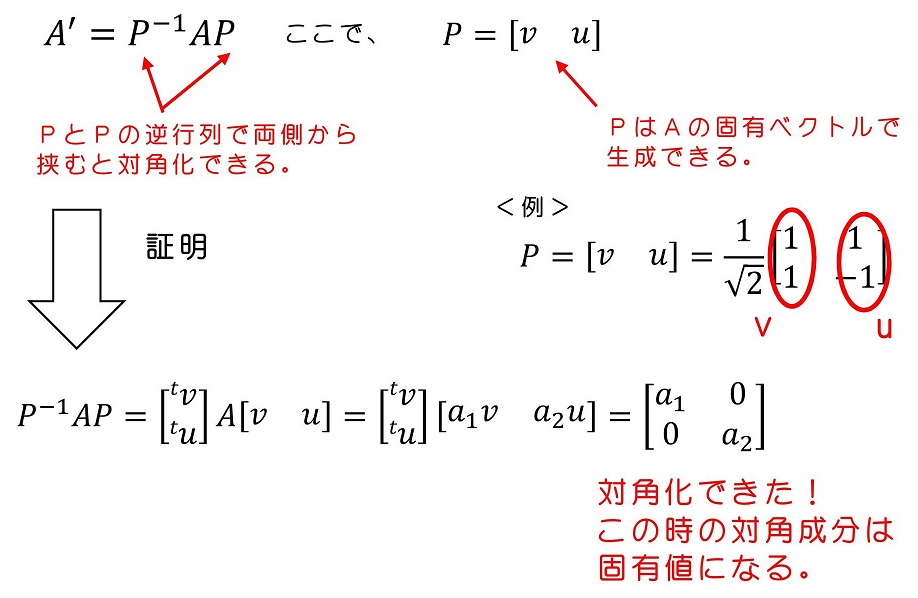
ここで、固有ベクトルおよびそれで生成される行列Pの『直交性』という重要な性質を用いた。冗長になるため、詳細は後で述べよう。さて、ここまで来てようやく微分方程式を解く数学的な準備が完了したよ。
【基準座標を導入しよう】

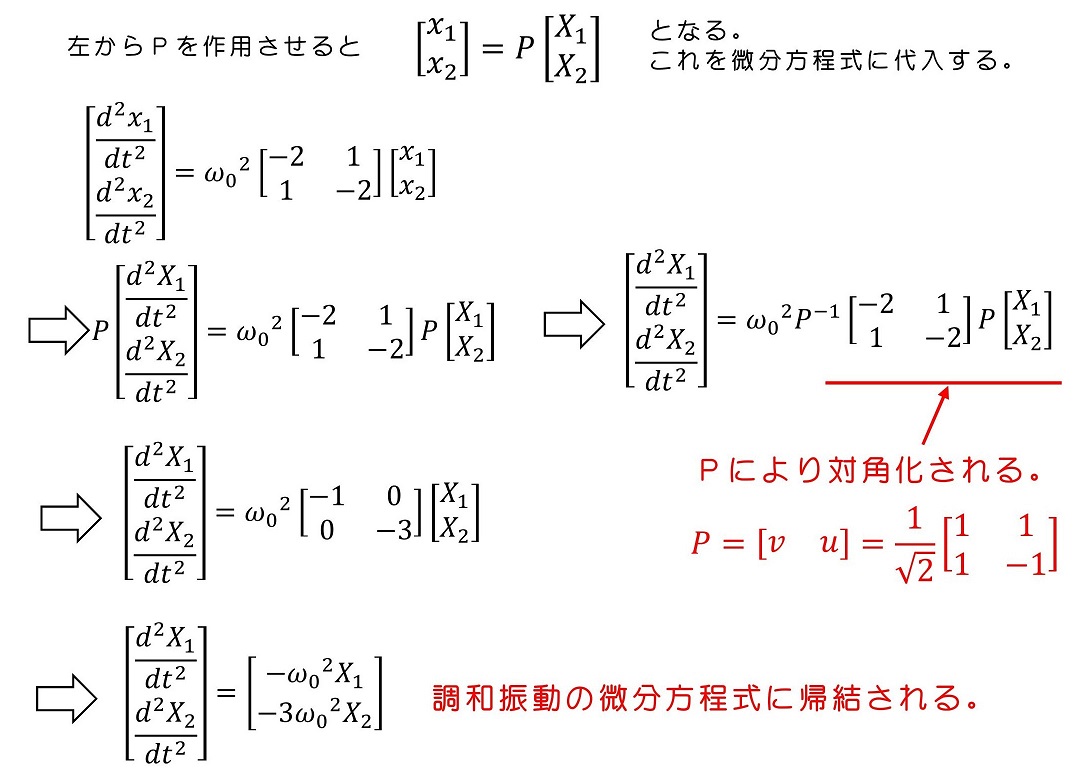
最初に座標変換を行い、基準座標という概念を導入することで、調和振動として微分方程式を解くことができるようになったよ。
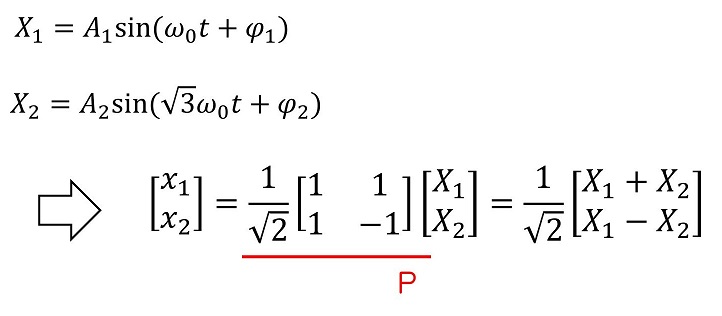
運動を解釈しよう
玉1の運動と玉2の運動は、直感的には複雑に動くような気がする。だが解いてみた式を解釈すると、実はシンプルに表すことができて、ω0の振動と√3ω0の振動の重ね合わせで表現できる。