9.1 重心と相対座標
万有引力を伴う天体現象を扱いたい。天体運動の中で最も簡単なのは2体の運動になる。2体はそれぞれ運動方程式に従って、運動する。2体の運動を第三者的な視点で見つめていると、互いが互いの周りをまわりながら、運動するという、非常に複雑な運動をしているように見えてしまう。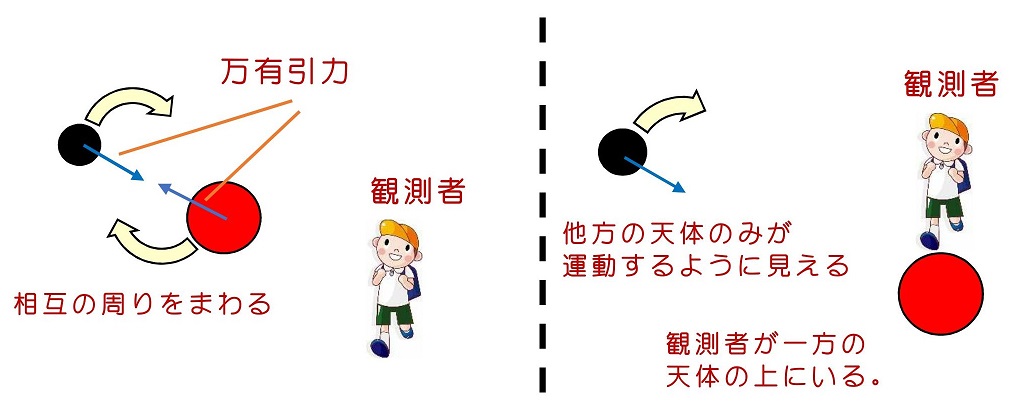
しかし、一方の天体の上に自分がたっており、もう一方天体の動きを観測する場合、運動はかなり簡易になる。このことを示したい。そのためには、相対座標と重心座標という考え方を導入する必要がある。
相対座標と重心を定式化する
天体1がr1の位置に存在し、天体2がr2の位置に存在していたとしよう。また、天体1、天体2の質量はm1、m2としよう。天体2から見た天体1の相対位置、二つの天体の重心はどうなるだろう?
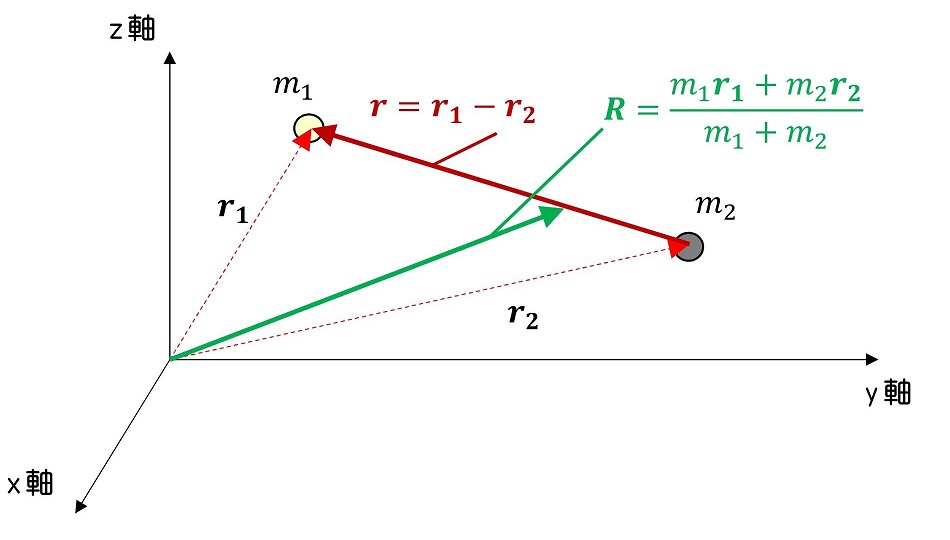
重心は天体1、天体2の間をm2:m1に内分する点である。重心の定義は『重心位置からの腕の長さ×その先端の質量が、すべての質点に対して等しくなるような位置』である。
運動方程式を重心と相対座標を用いて表そう
運動方程式はr1およびr2に関する方程式である。相対座標と重心座標の式を連立させることで、r1とr2をrとRで表現することができる。
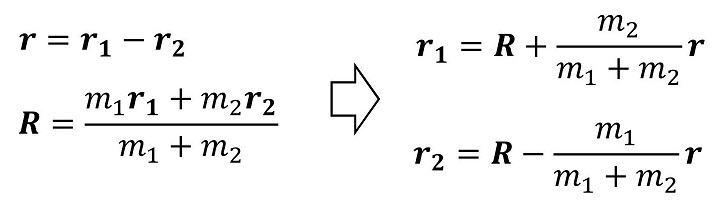
運動方程式
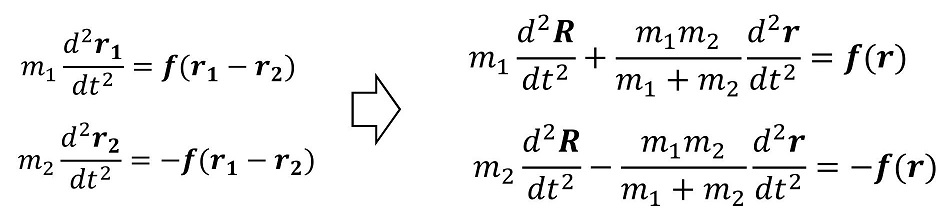
ここで両天体に働く力は内力fのみであり、その大きさは両天体の相対位置にのみ依存するとした。(万有引力がまさしくこれに当てはまる)天体1と天体2に働く力は、作用・反作用の法則により大きさは等しく向きは逆だ。
単純にこのままの方程式ではあまり意味のある方程式にならない。少し変形してみよう。

非常に有意な結果が得られたね。2式を足して得られた式は、重心座標の運動を表し、引いて得られた式は相対位置の運動を表している。今回の例では外力を考えなかったため重心は等速で変化することがわかる。一方、相対位置は万有引力の影響で運動する。相対位置の運動を表す運動方程式上の質量は、m1でもm2でもない、換算質量μになっている。
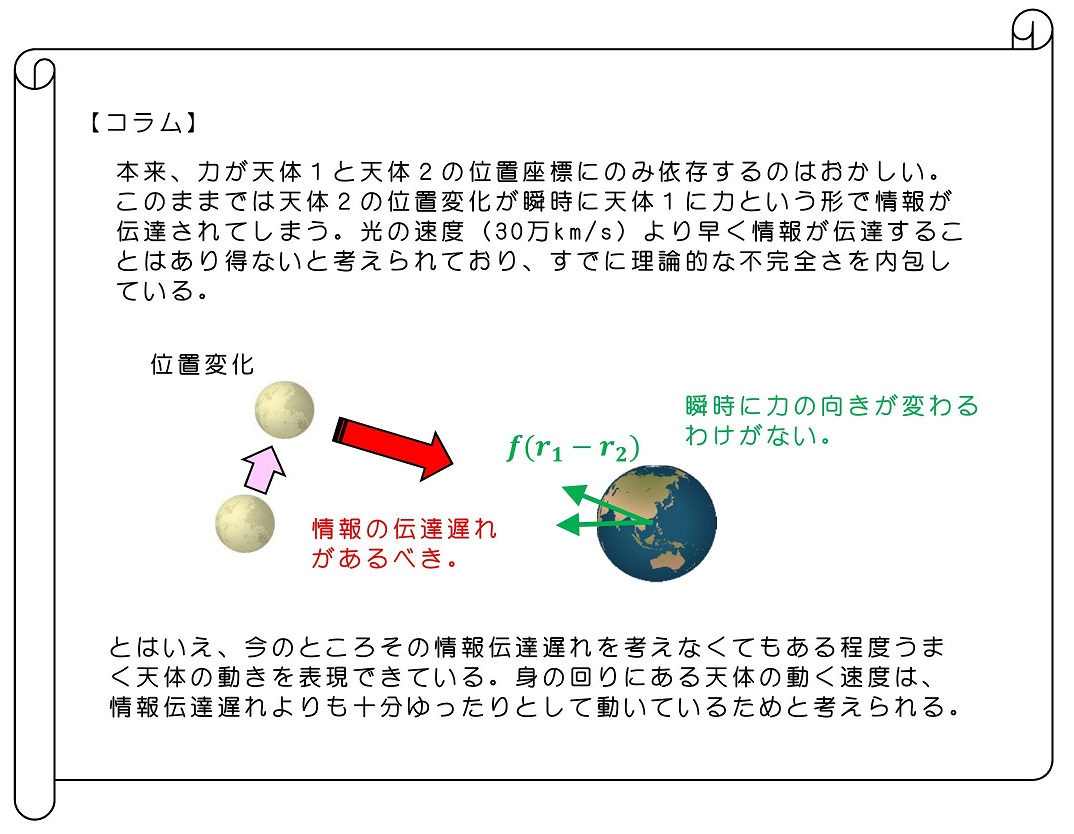
2体を各々の運動方程式で考えたときは、力が両天体の位置に依存するため、一方の運動が他方の運動に常に影響を与えており、複雑に運動するように見える。だが、天体2から見た天体1の運動は、換算質量の物体に、万有引力が働いた場合の運動方程式と完全に一致する。かなり簡易的に理解できるわけだ。
9.2 運動の極座標表示
さあ、今までは運動をxyzの座標系で考えてきていたが、天体運動のような回転運動を考えるときは、極座標を使うと記述しやすい。なぜならば、原点からの距離および原点周りの回転角によって座標を表すほうが、回転運動をうまく表現できるからである。そればかりでなく、慣性力の一種である遠心力など、非常に重要な概念も極座標表示を利用すれば自動的に算出できるようになる。とはいえ、極座標表示に移行するのはあまり簡単ではない。その理由を簡単に説明しておこう。
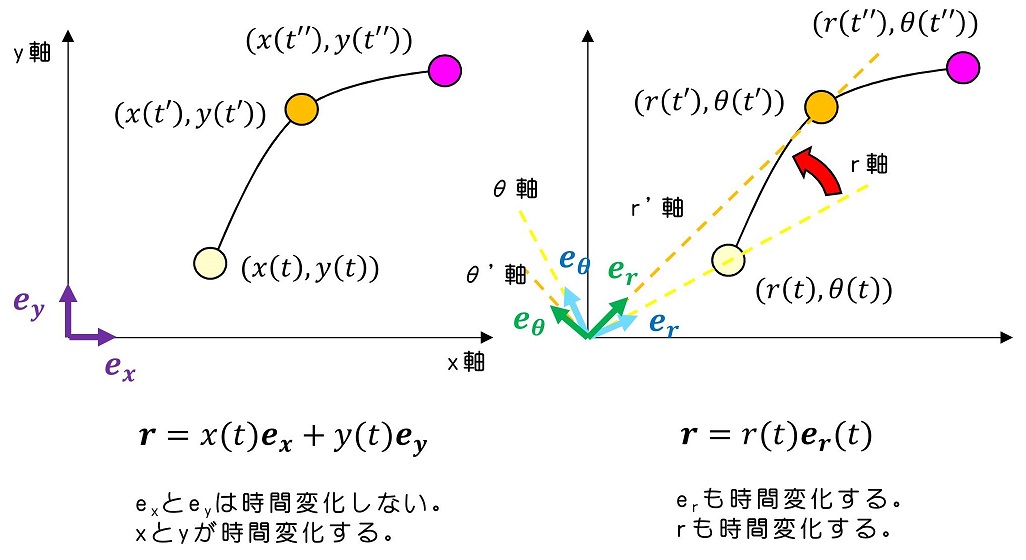
今、rベクトルは単なる座標を表すわけではなく、運動の軌跡に沿った位置変化を表している。x-y座標では時間変化分をxとyに押し付けて、単位ベクトルは変化しないと考えていたが、r-θ座標では単位ベクトルまでも時間変化すると考える。

極座標系での時間微分を計算しよう
運動方程式は微分方程式である。極座標表示を運動に導入するためには座標の微分を行わねばならない。どうなるか?
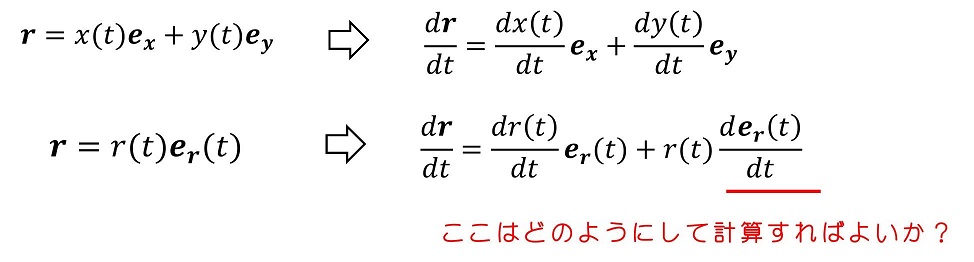
単位ベクトルが時間依存すると、単位ベクトルの微分が存在するので、erの微分をerとeθで表す必要が出てくる。どのようにすればよいか?
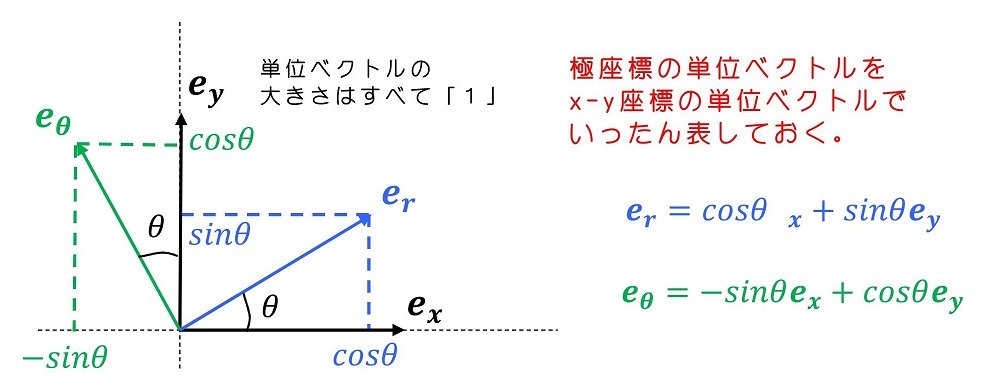
exとeyは時間変化しないことを考慮に入れて、erとeθの時間微分を計算しよう。
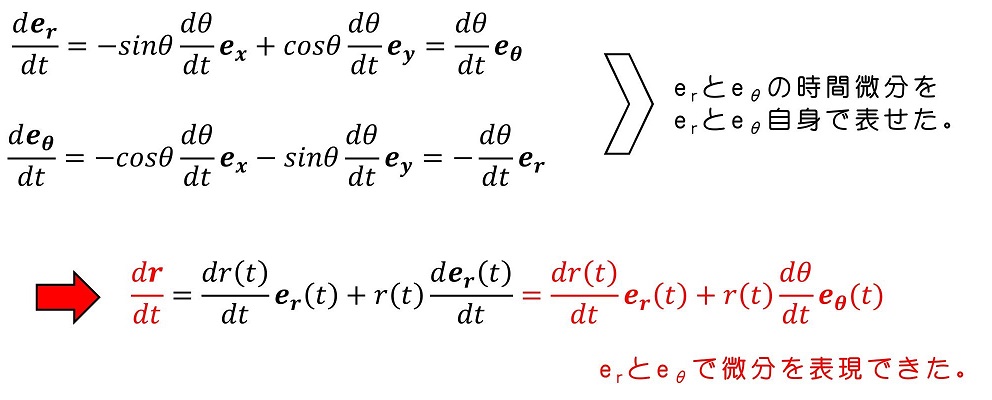
微分方程式は2階微分のため、さらに微分をしよう。

ここまで来て、運動方程式を極座標で表示できるようになった。

er方向とeθ方向は完全に独立である。そのため、等式は両辺のer成分およびeθ成分が一致しなければならない。

9.3 運動方程式を解釈しよう(θ方向)
運動方程式がかなり簡略化してきたことはわかるかい?当初はx-y座標を用いて2体それぞれの運動方程式を考えていたわけだが、それを重心運動と相対運動に分解し、内力しか働いていないときは、重心は等速運動することがわかった。相対運動をさらにr方向とθ方向に分解すると、実際に内力が関与するのはr方向のみであることがわかった。θ方向は、実は非常に重要な保存則を表している。角運動量を重心座標と相対座標で表そう
唐突だが角運動量を考えてみよう。

内力しか働いていない系のため、天体1と天体2の角運動量の総和は保存する。また、内力しか働いていない場合、重心は等速直線運動もしくは静止していると考えられる。一般に、重心の角運動量はゼロではない。だが、原点を特定の位置に選ぶことによって、重心の角運動量をゼロにすることができる。
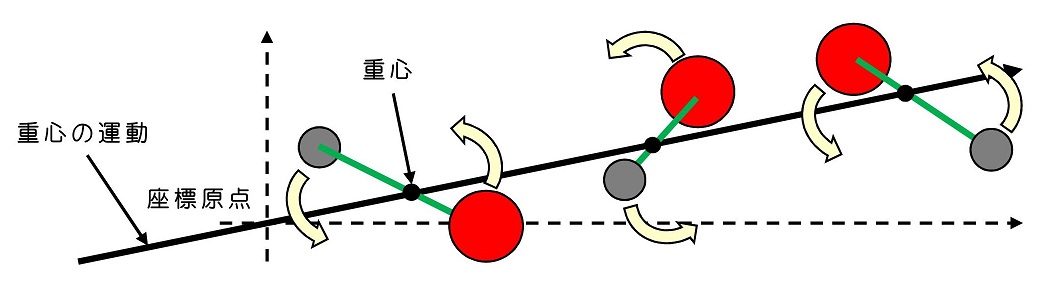
重心は直線運動をするため、その運動の軌跡上に座標原点をとる。(原点は別にどうとっても良い)こうすると、重心の位置を表すベクトルと、重心の速度を表すベクトルは平行になるため、重心の角運動量はゼロになる。

相対角運動量を極座標で表そう

さて、角運動量を微分しよう。ここで、ezは時間依存するか?今はrとθ方向の単位ベクトルは時間とともに変化しうることを想定しているが、ezはexやeyと同じように時間変化しないと考えられる。そのため、ezの時間微分はゼロである。すでに、相対角運動量が保存することは結論づいているため、微分したらゼロになるはずだね。
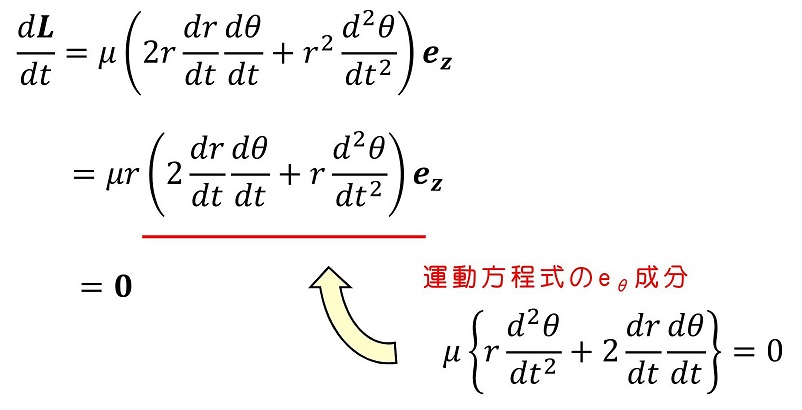
確かに、相対角運動量の微分がゼロになり、保存することがわかった。この時利用したのは運動方程式のeθ成分である。運動方程式のθ成分は、角運動量保存の法則を担保している。
運動方程式は、運動をする物体の座標の時間変化を求めるのに利用される。相対角運動量が保存されることを用いて、回転角の時間変化を求めることはできるだろうか?

9.4 運動方程式を解釈しよう(r方向)
さあ、いよいよ運動の本筋である、運動方程式のr方向成分の解釈を始めよう。ここでf(r)は万有引力を表す。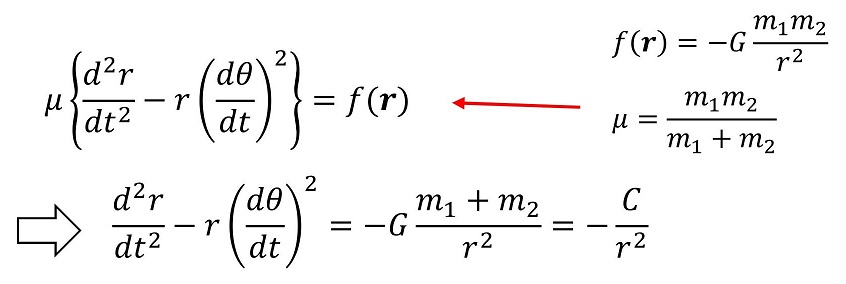
ここで要注意なのは、f(r)がマイナスであることだ。天体2から見た天体1の方向をプラスに定義するため、引力(天体1を引き寄せる側の力)はマイナスになるよ。今、万有引力定数や2体それぞれの質量は一定値のためすべてまとめてCとおくよ。
実は、さらに表式の中で固定値になりうるものがある。それは何か?角運動量が保存するわけだった。これを用いよう。

さあ、これでrの微分方程式が求まった。もしこの微分方程式を解くことができれば、rの時間発展が求まり、θの時間発展も求まる寸法である。しかしこの2階1次非斉次の微分方程式を解くのは非常に難儀である。
万有引力による運動を考える際に、むしろ重要になってくるのは、rとθの関係式である。rとθは媒介変数tによって関連付けられているとするわけである。これにより求まるのは極座標方程式である。今、求まっている次の2つの方程式に対して、知らないとなかなか思いつかない、テクニカルな式変形を行うことで、極座標方程式を求めることができる。

rをuという変数に変換して2式を連立させると、媒介変数であるtが消去され、uとθの微分方程式に変形できる。この方程式は非常に簡易な解をもつことが知られている。

①斉次方程式の一般解の求め方

②非斉次方程式の特解の求め方

③非斉次方程式の一般解は?
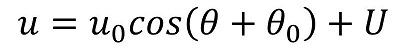
uをrに戻して式を整理しよう。
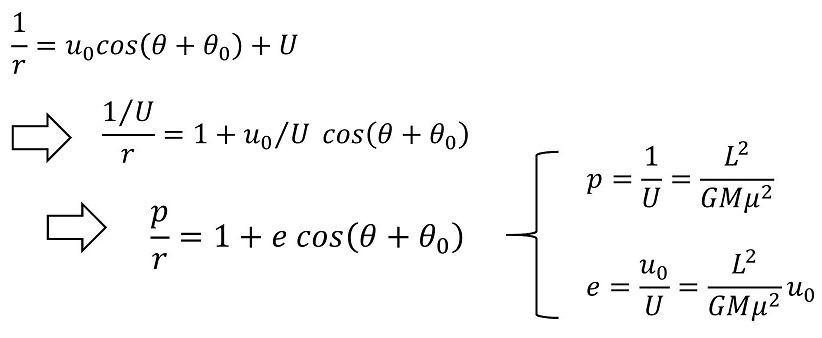
どのような系(質量や総角運動量)であったとしても、必ずrは正でなければならない。そのためには、u0≧0でなければならない。(一番上の式を見よう。例えば総角運動量Lが非常に大きいとき、Uはほぼゼロに等しい。u0がマイナスの値もとりうるなら、このような運動でrがマイナスになってしまう。)以上より、pは無論のこと、eも正の値orゼロをとりうる。
さて、微分方程式から始めた計算は、かなり特徴的な解まで到達してきたね。あと少しだ。実はこの解は『円錐関数』と呼ばれる図形群を一般的に表す、焦点を原点に持つ極座標の方程式になるんだよ。x-y座標系にするとわかりやすいね。変形しよう。
x軸からの変位角がΘ=θ+θ0となるようにx-y座標を選ぶ。

(1-e2)≠0の時
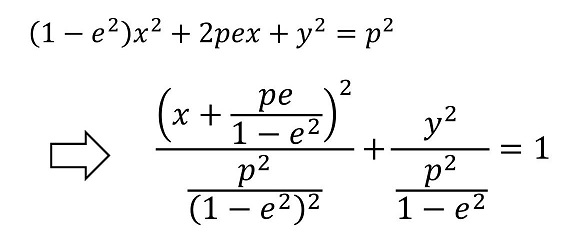
(i)e=0の時

(ii)0<e<1の時
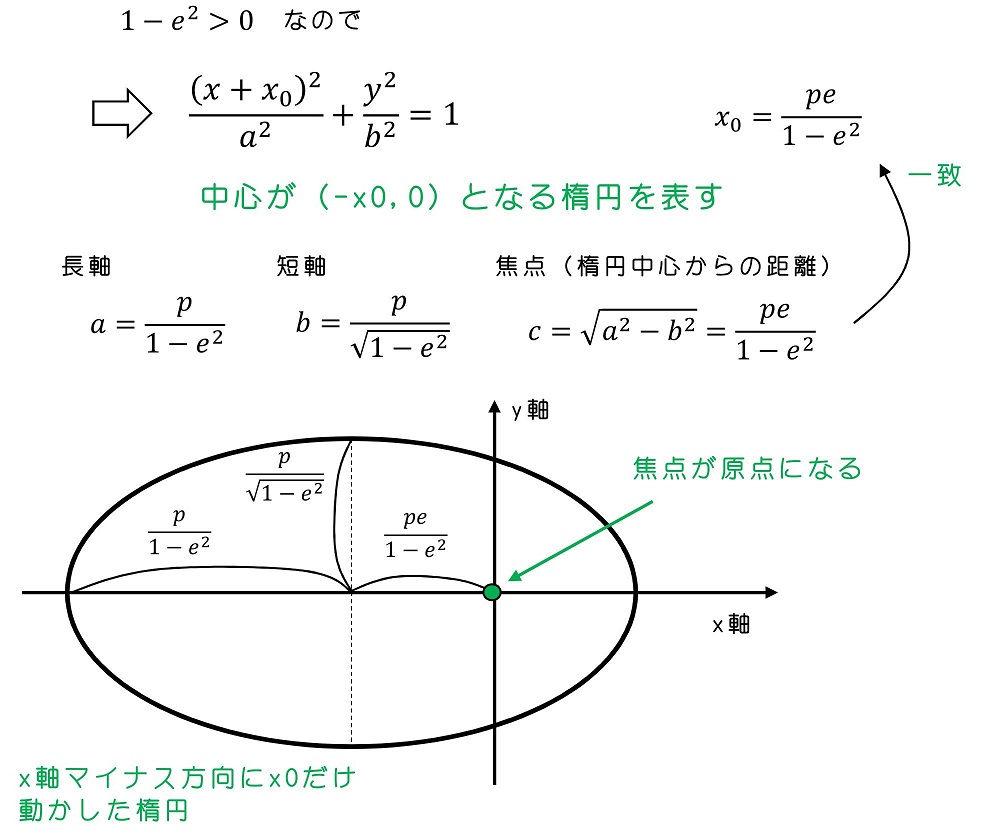
(iii)1<eの時
(1-e2)=0の時
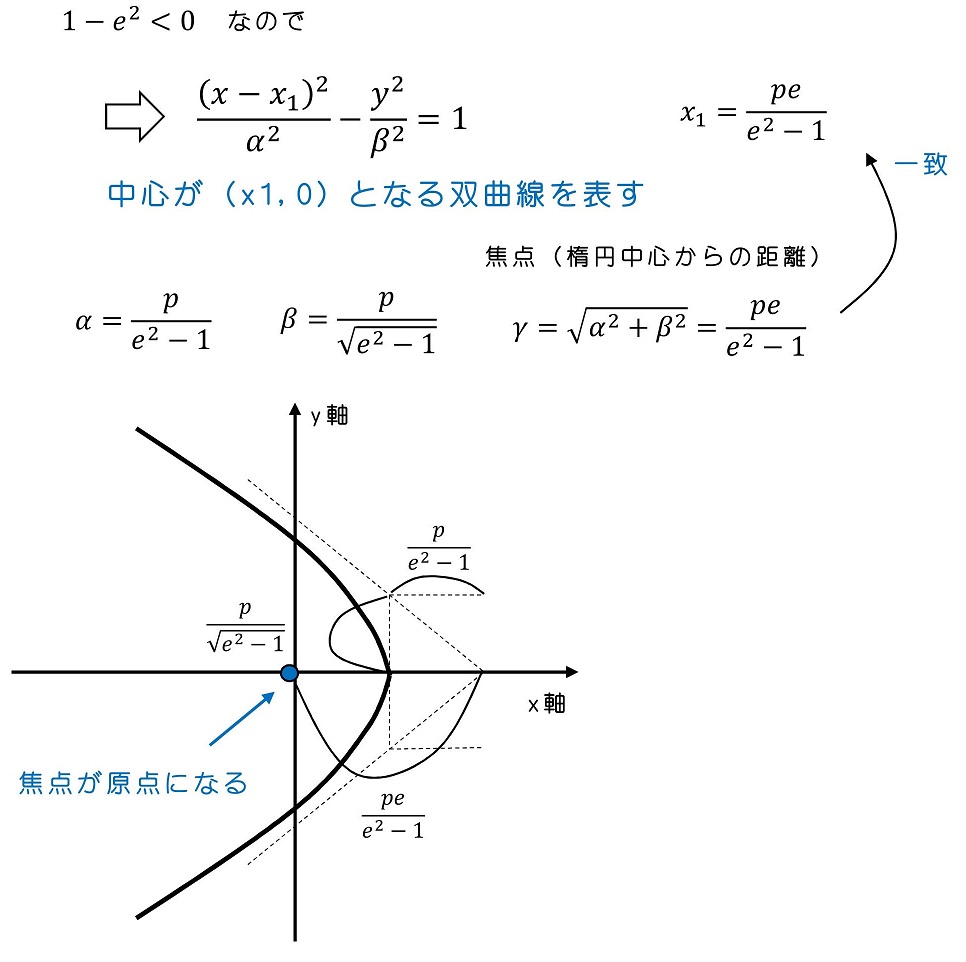
(iv)1=eの時
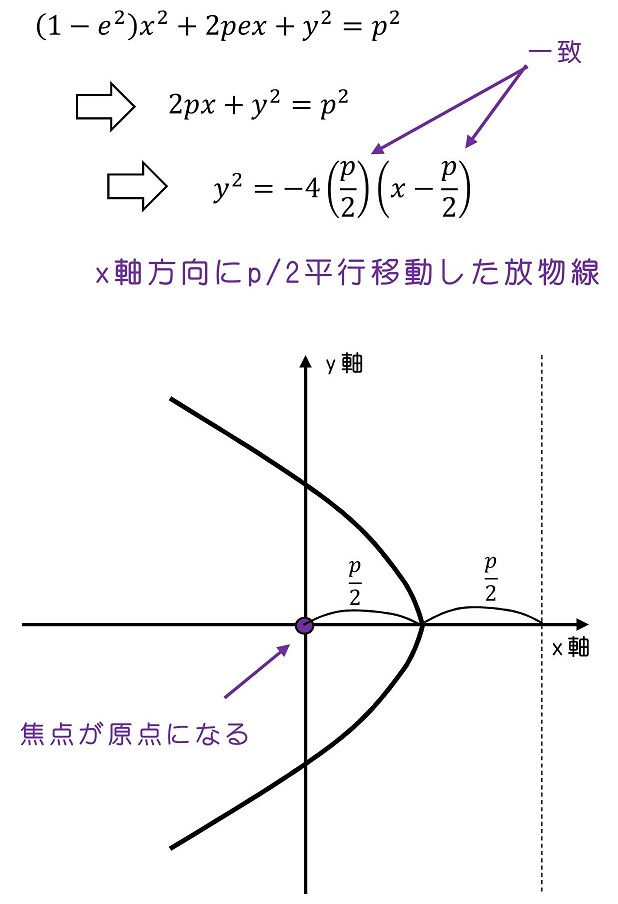
いわゆる円錐曲線とは、楕円(円含む)、放物線、双曲線のことを言う。
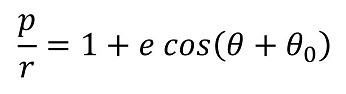
実際、この形の極座標表示では、必ず原点は焦点となる。eによって楕円(円)、放物線、双曲線のいずれになるかが決定され、pによって、半径などその図形のスケールに相当する値が決定される。eを離心率と呼び、pを通径と呼ぶ。
9.5 極座標表示を用いたエネルギー保存則
2つの万有引力の働く天体の運動を把握しようとしたとき、重心は等速運動をしつつ、相対的には『楕円(円)軌道』か『放物線軌道』、もしくは『双曲線軌道』を描くことがわかったよ。確かに時間とともに座標がどう変位していくのかはわからないが、軌跡を把握できたのは非常に大きな進歩だ。さて、とはいえ運動の軌跡が3パターンあることがわかったが、現実的に運動は1通りしか存在しないはずである。(急に物体が分身して3つの軌跡すべてを描くなんてことは怒らない)では『どのような』条件の時に、『どのようにして』3つの中から、1つの軌跡が選ばれるのだろうか?
軌跡が3つのうちどれを選択するかを議論するとき、エネルギー保存則を用いるとわかりやすいことが知られている。運動方程式や角運動量を極座標で表してきた。今度はエネルギー保存則を極座標を用いて表してみよう。まずは内力のみが働く2体の運動方程式を積分してみよう。
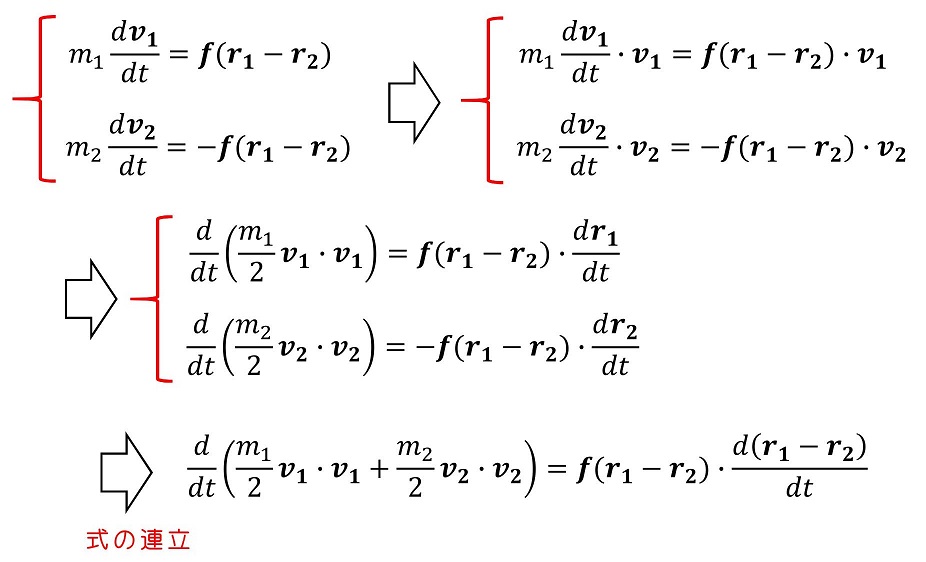
以上より、内力のみ働く2体のエネルギー保存則を導くことができる。
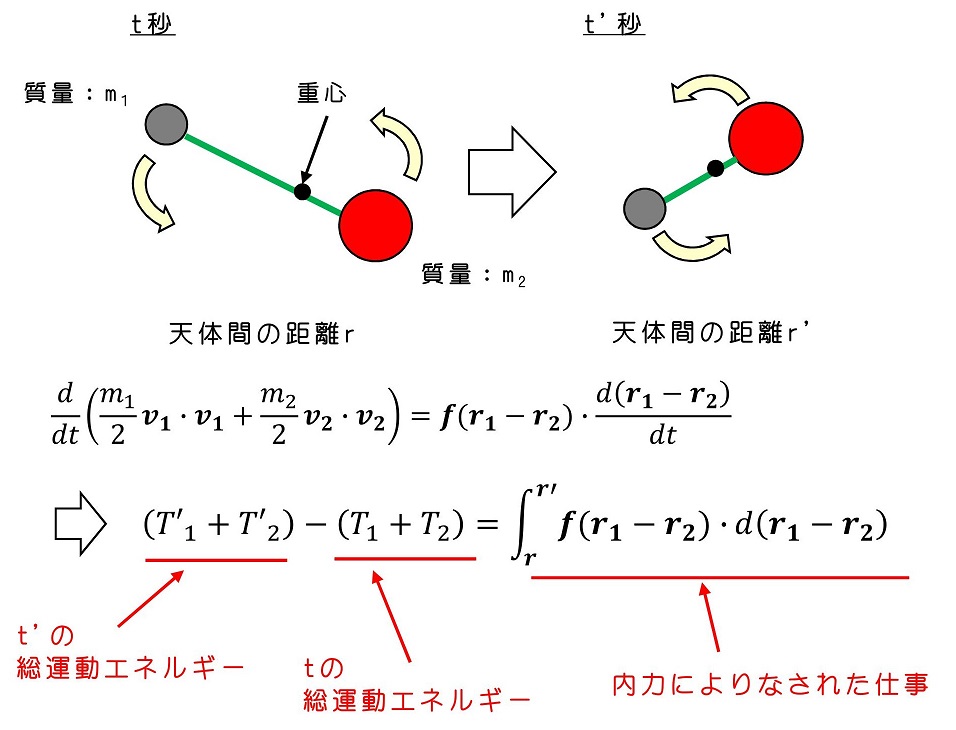
また、例のごとく内力によってなされた仕事を計算するのが、やっかいそうだね。ひとまずはここで重心座標と相対座標を導入したのち、相対運動に対して極座標表示を導入しよう。
運動エネルギーの総和
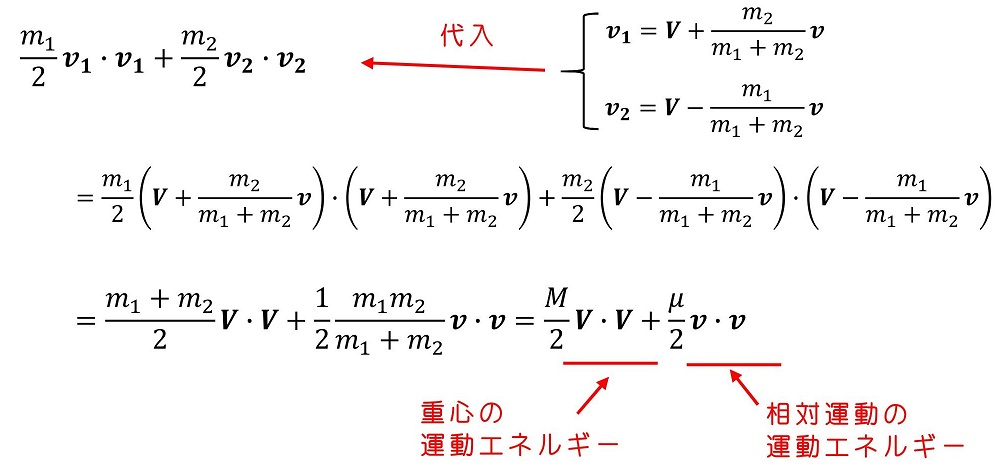
直感と一致する形になってくれるからありがたい。本来は天体1と天体2の運動エネルギーの総和だったが、実際分解してみると、『重心に全質量が集まって、重心速度Vで移動したときの運動エネルギー』と『天体2から見た天体1の場所に、換算質量μが存在していると考えたときの、天体2から見た天体1の相対運動エネルギー』になる。では、相対運動の運動エネルギーを極座標表示しよう。
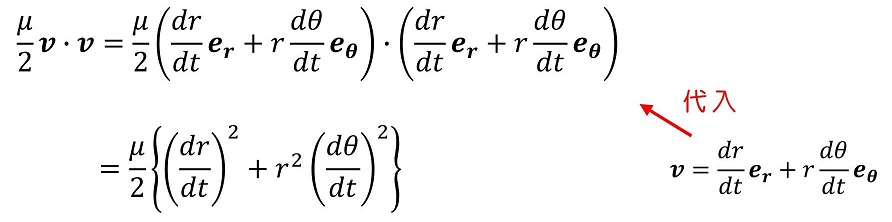
erとeθが直行する、それぞれ大きさ1のベクトルであることに注意しよう。ここで、相対座標での角運動量を利用してさらに運動エネルギーを変形しよう。

内力により2天体になされる仕事
さあ、次は仕事の部分だ。天体2から見た天体1の相対座標を用いて記述しなおそう。
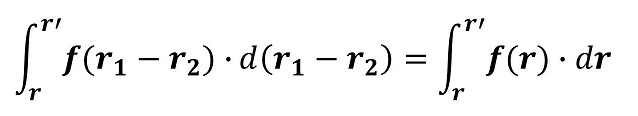
ここでf(r)に具体的な万有引力の式を導入しよう。万有引力は、r方向にのみ向きを持つよ。
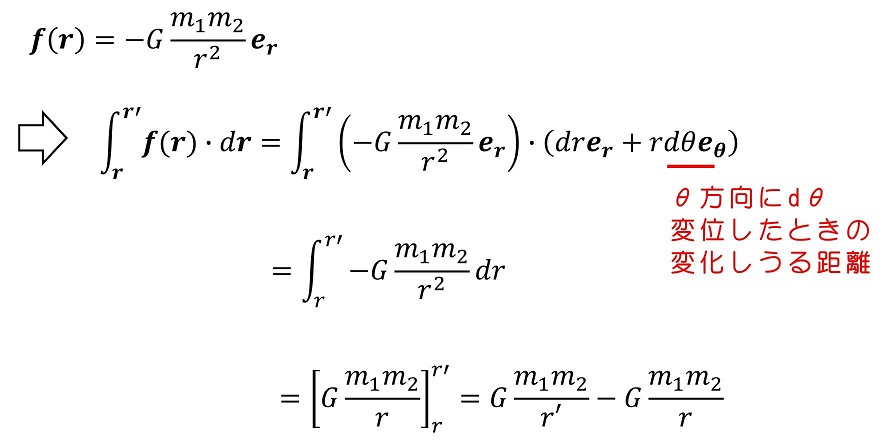
どのような経路で積分したとしても、仕事の値は変わらない。このため万有引力は保存力である。また、rに依存しするだけで、潜在的にエネルギーの底上げができるという、ポテンシャルエネルギーという考え方も導入できる。
力学的エネルギーと有効ポテンシャルエネルギーの導入
もう一度、エネルギー保存則を書き下そう。

またこの時、重心は等速直線運動を行っている。そのため、重心としての運動エネルギーは保存される。そのため、相対座標に関連した力学的エネルギーが保存すると考えればよい。
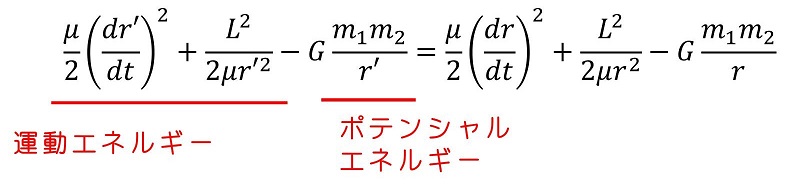
t'の時とtの時の相対運動に関連した力学的エネルギーが保存している。

もう一度、力学的エネルギーを見返してみよう。本来2体の相対運動部分は、2次元的な運動である。(r方向とθ方向が存在する)しかし、力学的エネルギー保存則の式の中に、θは出てきているだろうか?もともとはθが存在していたが、角運動量が保存するという条件を用いることで、θ成分が消去され、あたかもrのみで記述される運動とみなすことができる。角運動量の項は位置によって一意に決定されるポテンシャルエネルギーとみなすことができるのである。
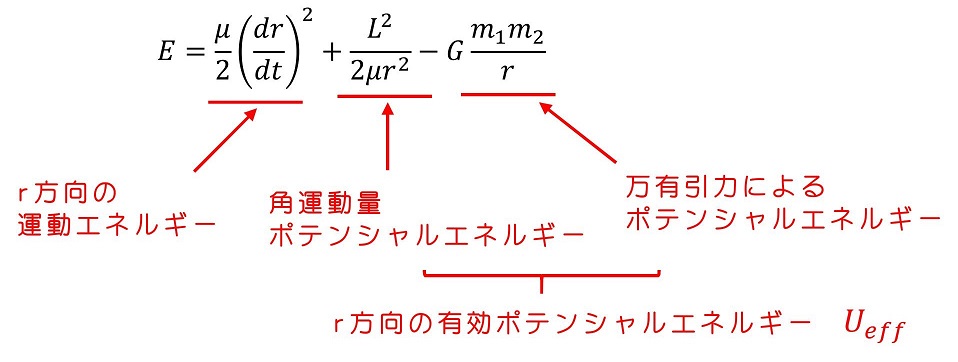
【エネルギーのグラフ】
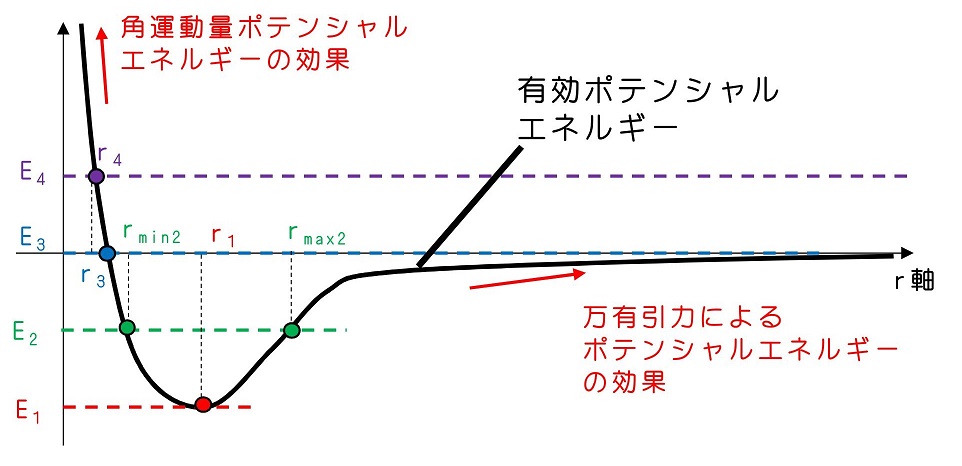
角運動量ポテンシャルと万有引力ポテンシャルの合計を、r方向の運動として有効に働くポテンシャルとみなせるため、有効ポテンシャルと呼ぶ。有効ポテンシャルをグラフとしてプロットすると、極小値を1つもつ形状になる。rが大きいときは、マイナス側からゼロに近づいていく。これは、万有引力ポテンシャルの効果が強く働くからである。一方、rがゼロに近づくと、+∞に近づいていく。これは、角運動量ポテンシャルの効果、つまり角運動量は保存するわけだから、rがゼロに近づくときは原点周りの速度がより早くなる。これによりエネルギーの潜在的かさ上げ量が増えていくわけである。
ここまできて、運動の軌跡が『楕円(円)』『放物線』『双曲線』のいずれに合致するかは、力学的エネルギーの大きさE1~E4と、有効ポテンシャルのグラフ形状により、把握することができる。
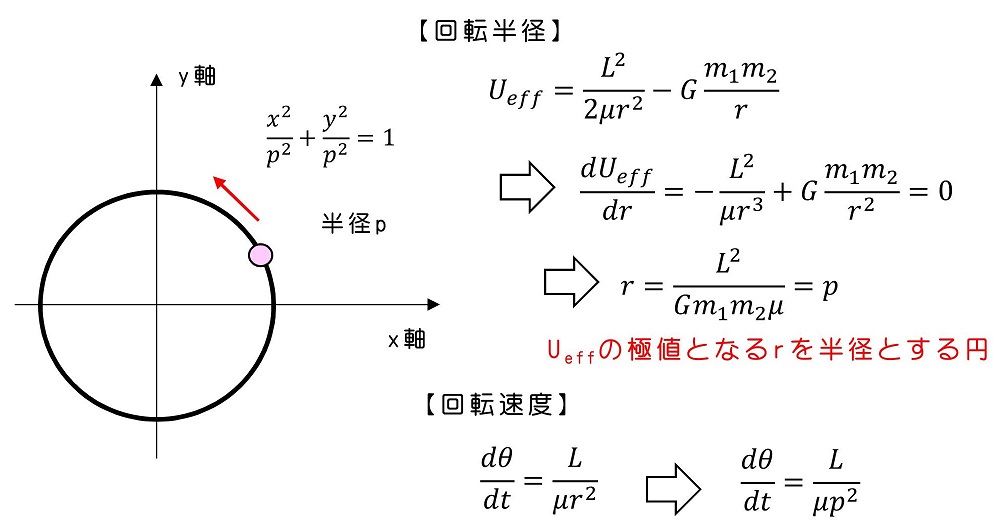
力学的エネルギー=E1
今、有効ポテンシャルがr→∞でゼロに収束する。力学的エネルギーがマイナスとは、有効ポテンシャルの影響を受けないはるか遠くに物体が存在しえると仮定すると、r方向の運動エネルギーがマイナスを表す。しかし、運動エネルギーは必ず『プラス』であるはずである。つまり、r→∞にいくと仮定すると、エネルギー保存則の式が成立しなくなるため、仮定は物理的に反する運動になる。こんな運動は存在しえない(r→∞に行けない)ということになる。ではどのような場合が存在しうるか?
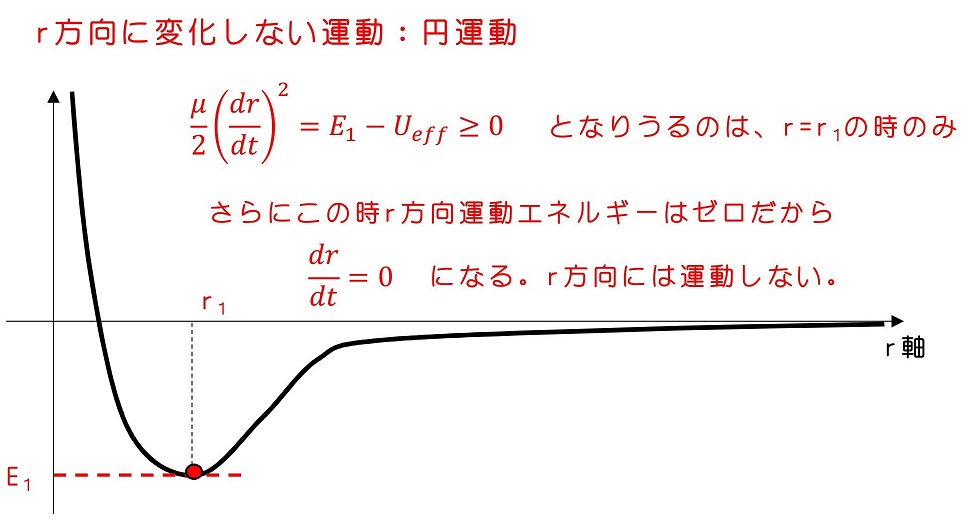
もちろん、r=r1のみが存在しうる唯一の軌跡で、この時のr方向の運動エネルギーがゼロだからと言って、物体が一切動いていないわけではない。r方向の運動エネルギーはゼロだが、θ方向の運動はしているわけである。r方向の運動エネルギーがゼロとは、r方向に変位しない、つまり径が常に一定で動き続けるというわけだ。
力学的エネルギー=E2
同様の考察をおこなう。今、力学的エネルギーがE2の時もやはりr→∞はr方向の運動エネルギーがマイナスとなり不可能な運動となる。ただ、エネルギーがE1のときよりかは、r方向に自由の利く運動になる。
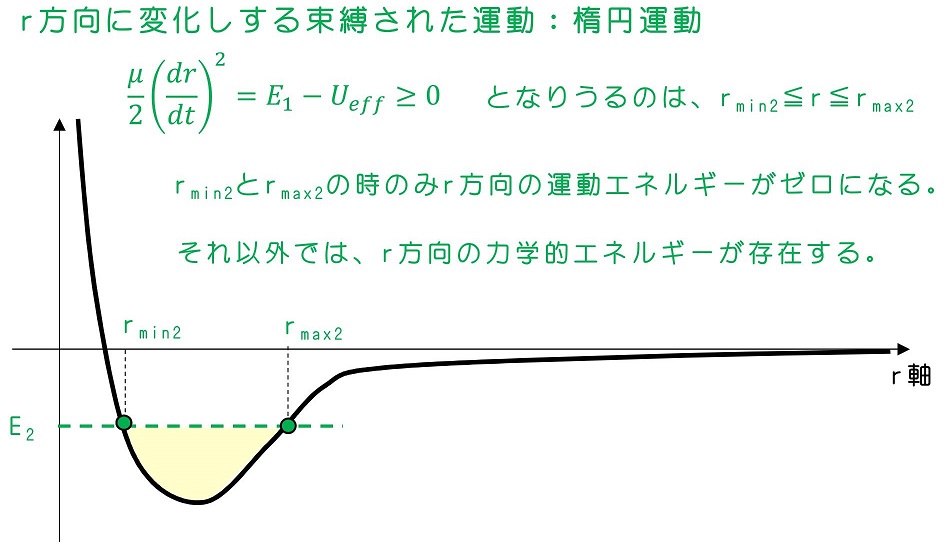
エネルギー保存則を用いるのみでは、とりうるrの範囲がわかるだけで、実際の運動軌道まではわからないが、すでに軌道は『楕円(円)』『放物線』『双曲線』のいずれかをとるとわかっているため、束縛という条件のみで『楕円』と考えることができる。
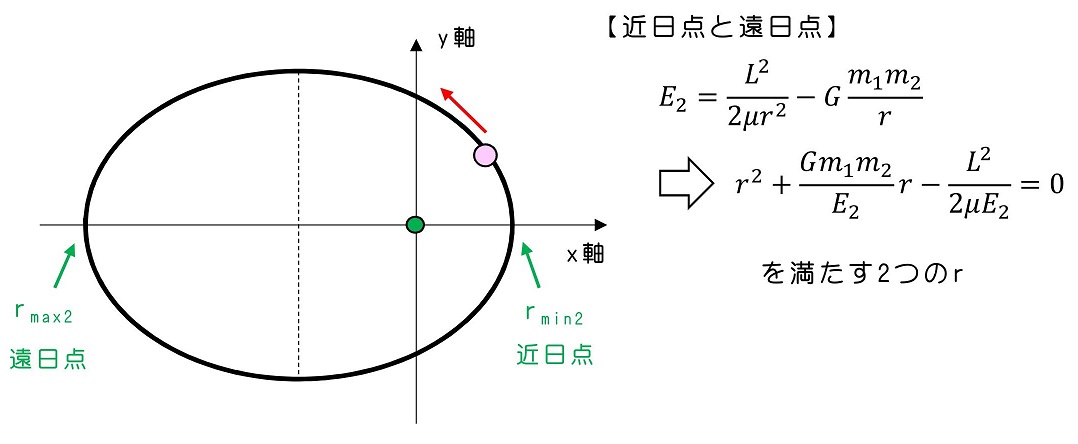
力学的エネルギー=E3とE4
力学的エネルギーがゼロになった瞬間に、ぎりぎりr→無限まで到達することができるようになる。楕円から双曲線に切り替わる瞬間であり、これが放物線軌跡になる。また、力学的エネルギーが正になると、無限遠に到達し、さらにその時のr方向の運動エネルギーも存在する。双曲線軌跡である。これは、無限遠での運動エネルギーが十分大きければ、中心に存在する天体2による力が足りず、束縛できないことを示している。
9.6 ケプラーの法則
ニュートン以前に、天体運動をつぶさに観察し、天体運動が満たすべき法則を発見した人物としてケプラーがあげられる。彼は3つの法則を提起した。ニュートンの運動方程式は、この3法則を包括するよう構築されているため、ニュートン力学を用いて、この法則を導くことができるはずである。
ここで、太陽や地球と限定せず、恒星や惑星と呼称しているところが肝心だ。すなわち、太陽系に限定せず、この世に存在するすべての恒星とその周りをまわる惑星について、①から③の法則が成立するわけだ。①はすでに証明済だから、②と③について議論しよう。まずは②についてだ。
②面積速度一定の法則とは?
まずは面積速度とは何かが不明だ。あまり聞かない概念だからね。
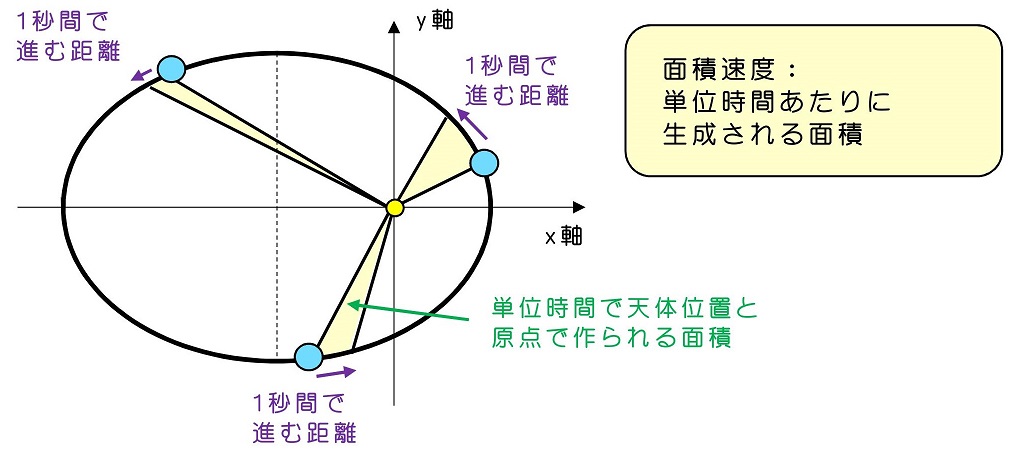
今、一般には楕円軌道を描きながら運動をする。それに伴い、原点からの距離が離れたり、近づいたりする。面積速度が一定になるためには、原点に近づいたときには単位時間で進む距離が長くなるべきであり、原点から離れたときは単位時間で進む距離が短くなるべきである。面積速度を具体的に表すと、次のようになる。
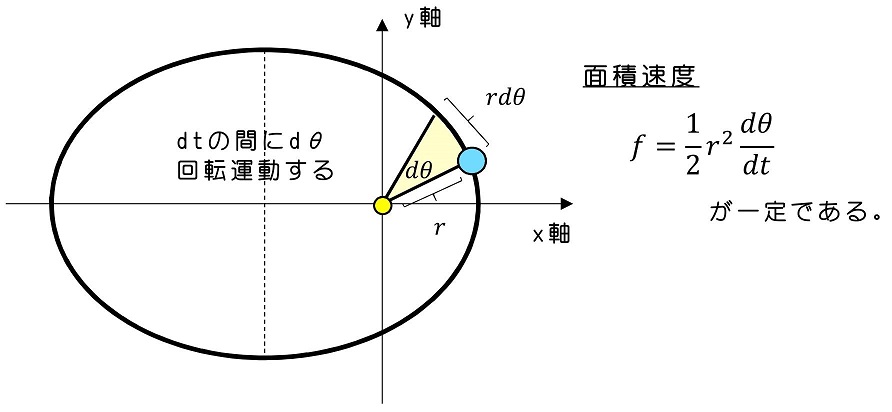
面積速度が一定ということは、角運動量保存の法則と密接に結びついている。
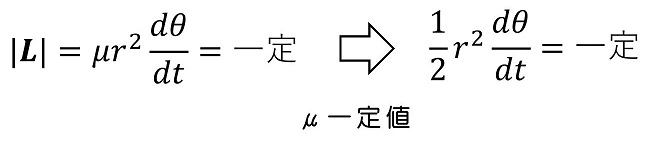
内力のみが働く場合、角運動量が保存する。面積速度も角運動量の大きさに比例する値であり、同じく保存すべきであることがわかる。
③T2乗がaの3乗に比例
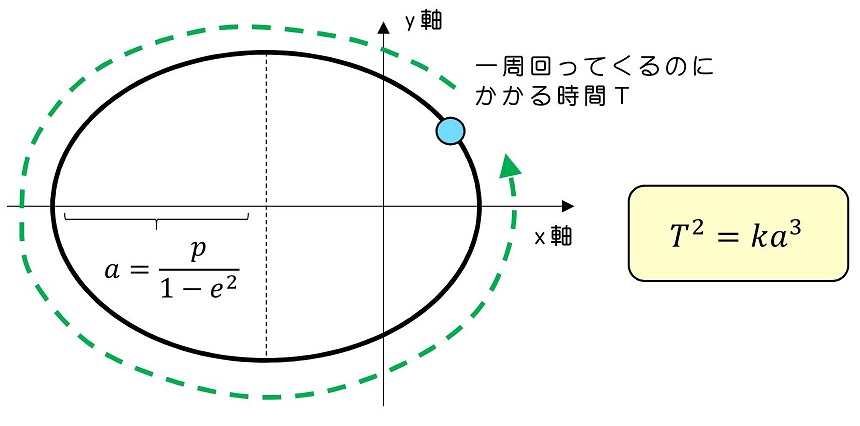
概念的にはそれほど難しくない。だがこれを運動方程式から証明するのは、面倒だ。実はラグランジュの運動方程式と呼ばれる、ニュートン方程式に同値な方程式を用いると、運動の相似性から証明可能である。とはいえ、そちらの証明はラグランジュ方程式の章に譲るとして、今回はただの円の場合、T2乗が半径の3乗に比例することを示そう。
角運動量保存の法則より、一周運動するときの周期を求めることができる。
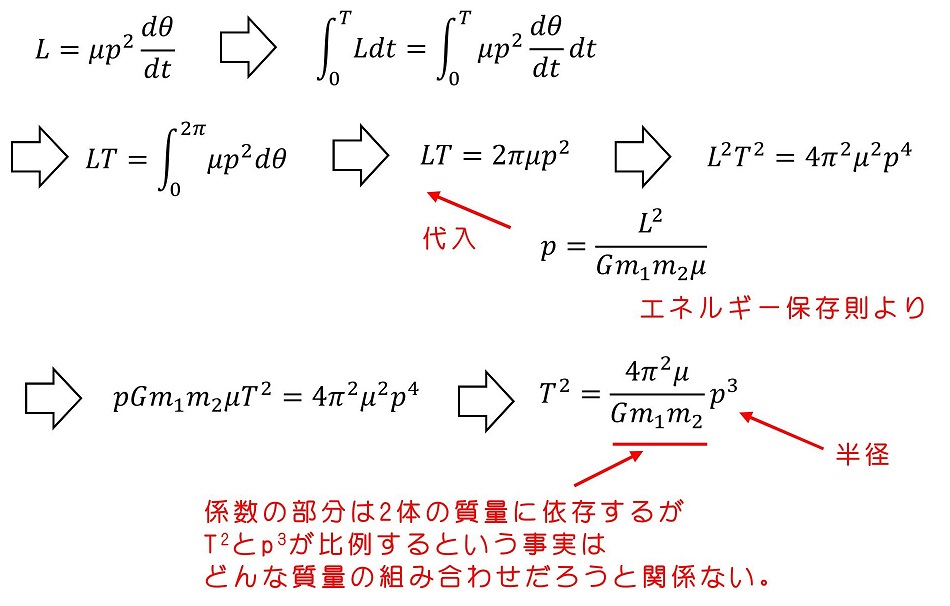
9.7 等速円運動
ここまでは、内力による運動の一般則を導くために、忠実に方程式を解いてきたが、より簡略化してもう一度運動を見直そう。
Ⅰ:太陽質量が地球よりもはるかに大きいことを模擬する。

Ⅱ:運動が完全な円軌道と考える。

ここで運動方程式、角運動量、エネルギー保存則をつぶさに観察しよう。
角運動量
角運動量は保存している。これは円運動だろうとなんだろうと関係なく、内力のみが働く系では保存することがわかる。x-y座標の原点を太陽位置とすれば重心もx-y座標の原点に存在することになり、相対座標の原点もx-y座標の原点と一致する。重心位置が原点のため、重心のの角運動量はゼロとなり、全角運動量とは、相対運動の角運動量と一致する。非常にわかりやすい構成となる。

エネルギー保存則
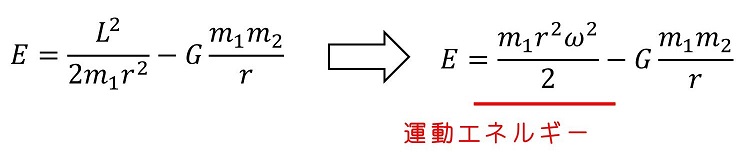
角運動量ポテンシャルとみなしていたが、実際はθ方向の運動エネルギーであった。今回はr方向の運動エネルギーは存在しない(rは一定)だから、有効ポテンシャルという考えを導入する意味はあまりない。角運動量ポテンシャルだった部分は、角振動数ωで等速円運動をするときの運動エネルギーを表している。
運動方程式
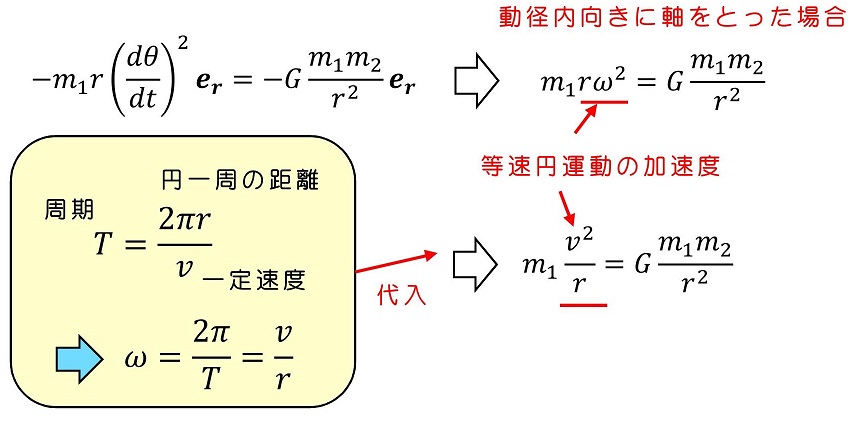
等速円運動の場合、角速度ωを円の半径と運動速度の大きさで表すことができる。運動方程式の加速度をrとωを用いて表現することもできるが、rとωを用いて表すこともできる。

運動を予想する
真横にロケットを打ち出した時、円運動をして戻ってくるような速度のことを、第1宇宙速度と呼ぶ。この問題は第1宇宙速度を求める問題である。ロケットの質量が、地球の質量に比べ非常に小さく、運動も円軌道になる。角運動量が保存するのは万有引力のある2体運動すべてに言えることであり、軌道半径が一定とすると、角速度も一定になる。このため、運動速度の大きさも一定である。重心が地球中心とほぼ同じ等速円運動になると期待される。等速円運動の運動方程式を用いればよい。
式をたて、解釈する
等速円運動の加速度はrとvを用いて表すことができる。力は万有引力である。今、軸を中心向き正にとる。
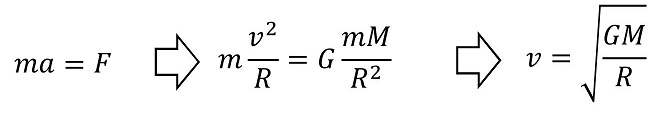
地球質量と万有引力定数、地球中心からの距離によって、等速円運動の速度が決まる。ちなみに、もしこれより速度が小さければ地面に落下し、これよりも大きかったら楕円軌道になる。
9.8 鉛直打ち上げ運動
簡略化のもう一つの運動として、鉛直方向への打ち上げ運動がある。例えば地球からロケットを鉛直情報に打ち上げる場合がそれにあたる。この時、運動方程式、角運動量、エネルギー保存則はどのように表されるか?
角運動量
rは変位するが、θは変位しない。そのため、角運動量はゼロになる。
エネルギー保存則
r方向のみの方程式になるが、角運動量ポテンシャルがゼロになる。
運動方程式
回転しないため、単純な1次元運動に帰結する。加速度もrの2階微分になる。
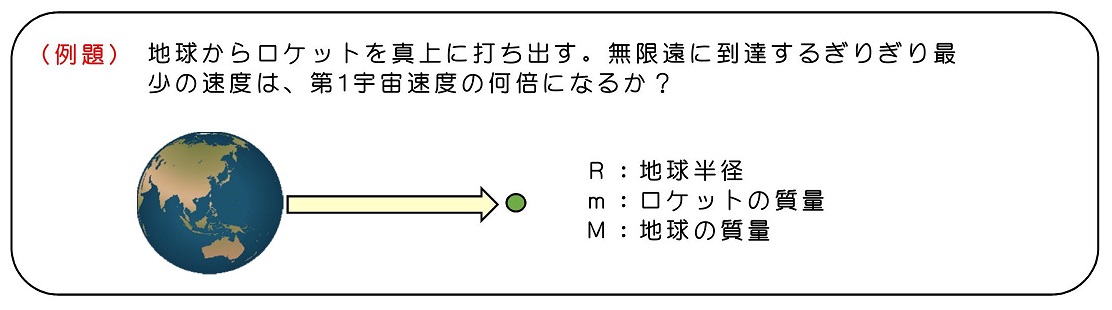
運動を予想する
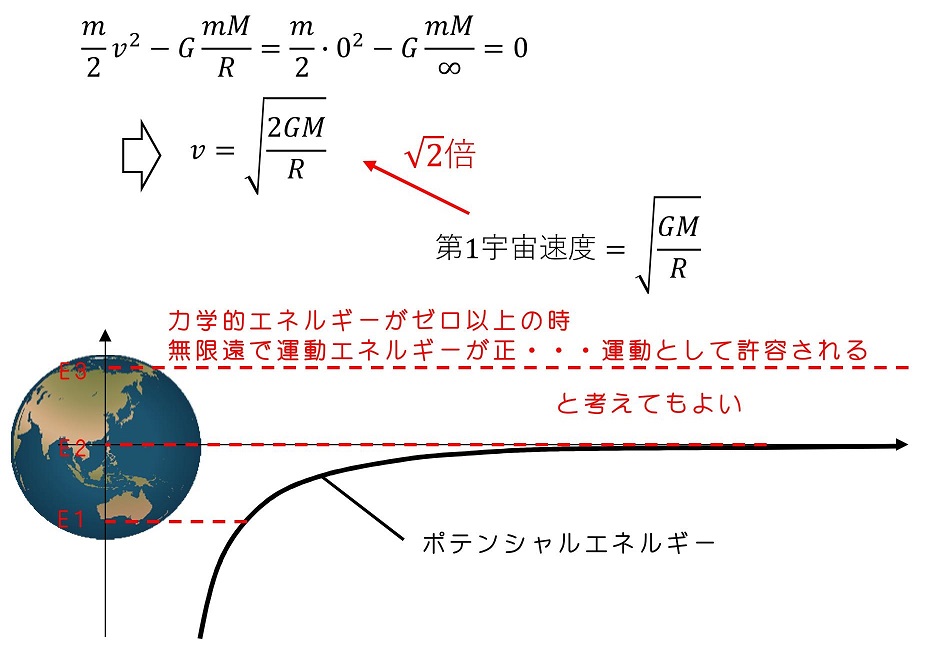
真上にロケットを打ち出して、ぎりぎり戻ってこない速度のことを第2宇宙速度と呼ぶ。打ち出す速度が小さいと、引力が存在するためある程度まで到達すると引き戻される。打ち出す速度を次第に増やしていくと、到達できる距離は遠くなっていく。いずれは無限遠に到達できるようになる。
式をたてて、解釈する
運動方程式の積分である、エネルギー保存則を利用したほうが簡単である。地球上から打ち上げるときの力学的エネルギーと、無限遠での力学的エネルギーで保存則をたてる。無限遠にぎりぎり到達できる状態を知りたいので、無限遠で速度がゼロになると考えればよい。