10.1 ガリレイ変換と相対性原理
座標を設定するときに、原点を空間の任意の場所に置き、好きなほうを座標のプラスに設定していた。こんなことをしてよかったのだろうか?地球の上に置かれた机の上で、箱が滑る運動を扱うときは、机の端を原点としていたが、本来地球は自転しているので、原点は動いてることになる。地球と人工衛星の運動を扱うとき、地球中心を原点に置いたが、地球は太陽の周りを公転しているため、原点は動いていることになる。地球と太陽の運動を考えるとき、太陽の中心に原点を置いていたが、太陽は銀河系中心の周りをまわっているため、原点は動いていたことになる。今まで設定してきた原点は、実は動く原点だったわけである。しかも、何かの周りを回転までしていたのである。
回転半径が非常に大きいため実質は原点が直線運動していると扱おう。直線運動をしている原点に対して運動方程式を考えてきた。原点は静止させなくてよいのだろうか?これを次のような問題に落とし込もう。
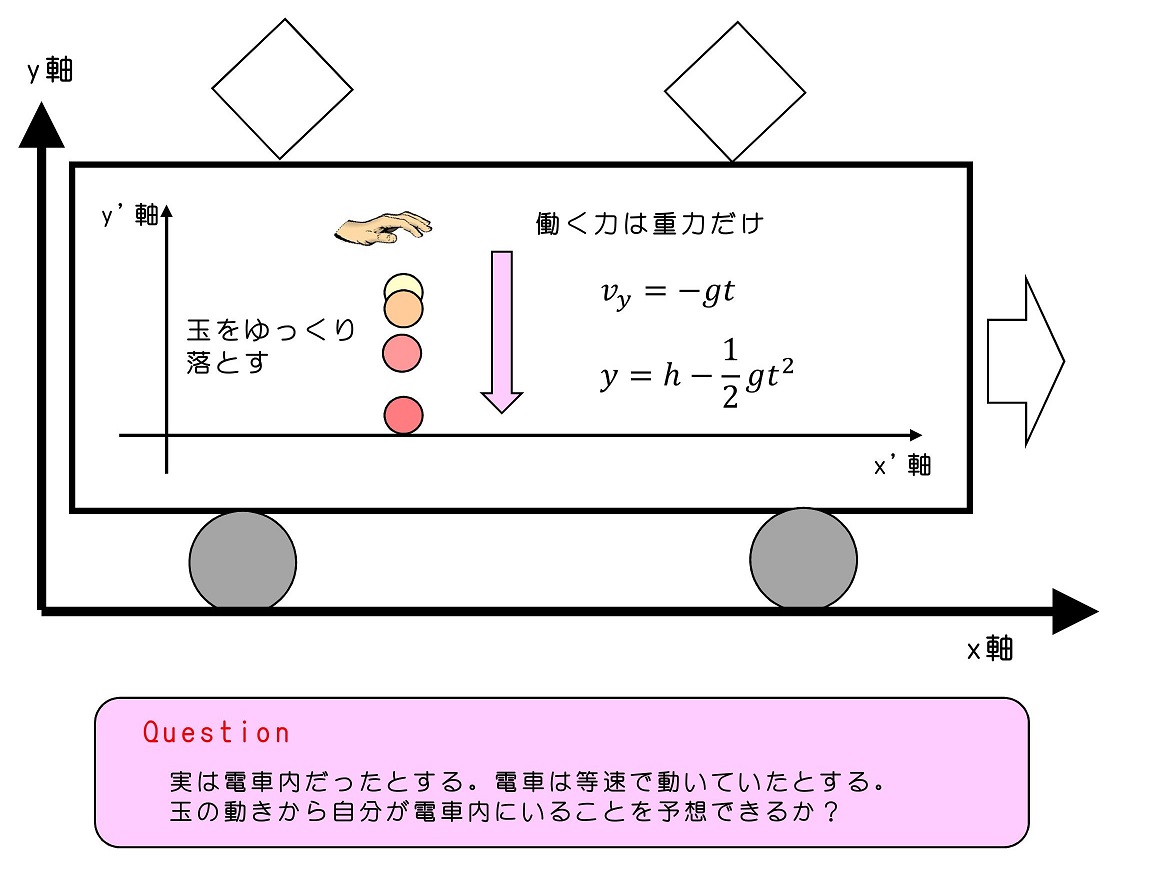
もし電車と一緒に動く座標系で考えても、電車の外部の座標系で考えても、運動の3法則が成立するのであれば、玉の動きから、自分が電車の中にいることを知ることはできない。

①慣性の法則の理解を深めよう
座標という概念を用いて言い換えよう。
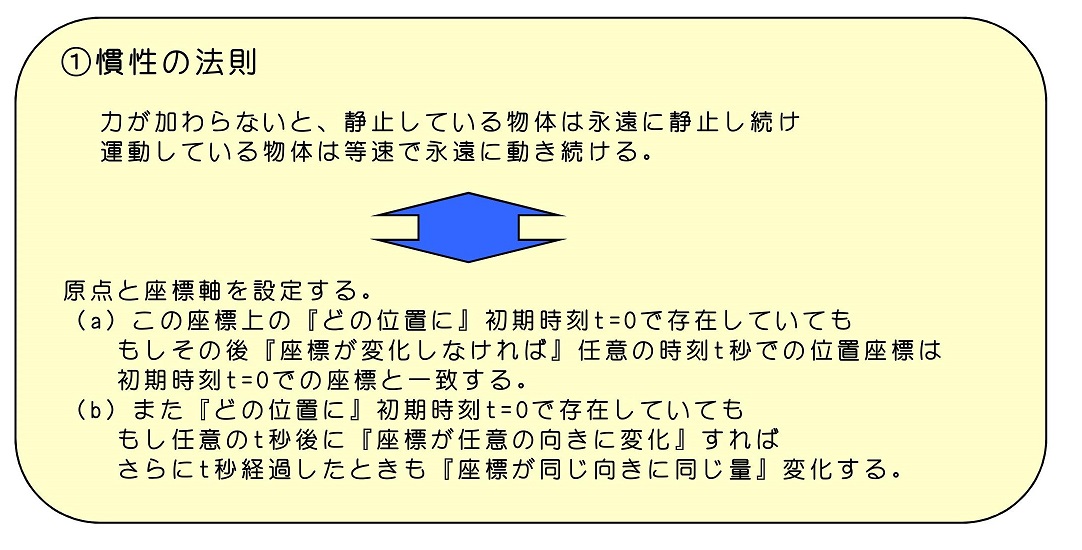
(a)よりいえることを考えよう。空間上に原点Oをとり、そこから座標軸を設定することで単位ベクトルex、ey、ezを考えることができる。座標上の物体が時間によって座標を変えないとはつまり、原点及び単位ベクトルが時間によって変化しない座標系を『考えることができる』ということである。
<反例>
もし、原点や単位ベクトルが時間とともに変化すると・・・
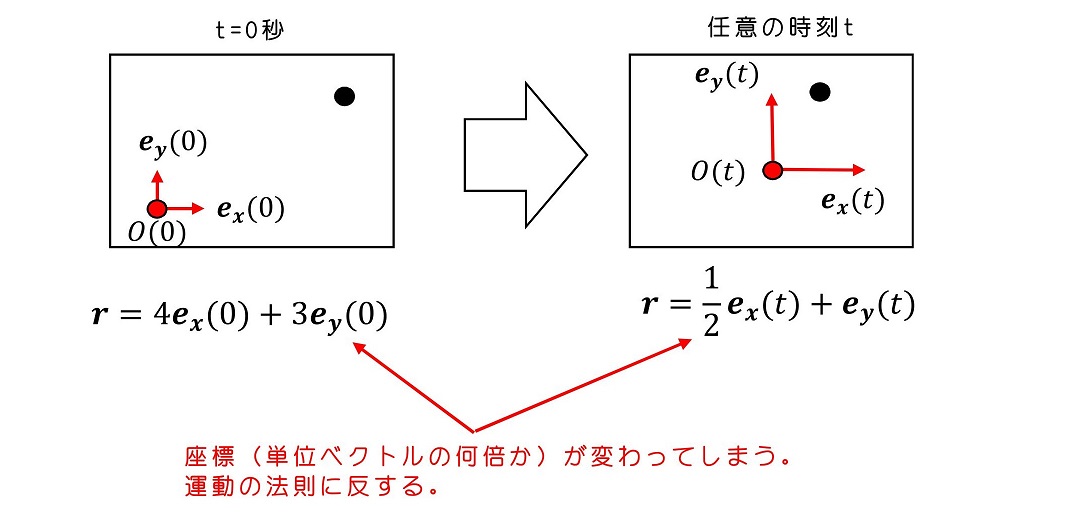
<反例>
もし、座標や時間が一様でなかったら・・・

一様なパラメータkを用いて座標と時間が次のように表せたとする。 この時、座標は時間は一様でない。(場所や時刻によって変化量が変わる)

また、(b)からは空間の等方性も結論できる。空間に特別な向きは存在せず、ある方向にt秒でl進めば、次のt秒でも同じlだけ進むような座標を『考えることができる』
<反例>
もし、座標が等方的でないと・・・
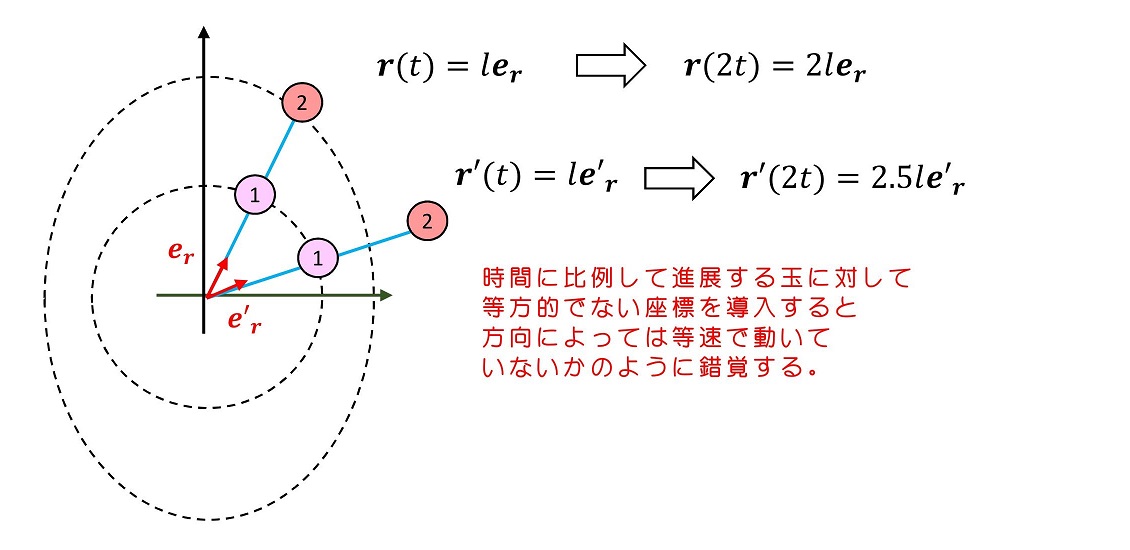
さて、注意すべきは原点が静止しており、単位ベクトルが時間変化せず、単位ベクトルの定数倍を表す座標値は一様かつ等方的であり、また時間も一様である系は『必須』ではなくて、『選択可能』ということだ。仮に、上記いずれかの条件がかけたとしても、運動の3法則が成立するのであれば、実質力学運動を表す表現方法として問題ないのである。
原点位置が時間変化する系は成立するだろうか?
単位ベクトルが時間変化せず、座標は一様等方で、時間も一様であるが、原点が時間とともに等速で移動するような系は運動の3法則を満たすか考えよう。(力学運動を表す表現方法として問題ないか?)
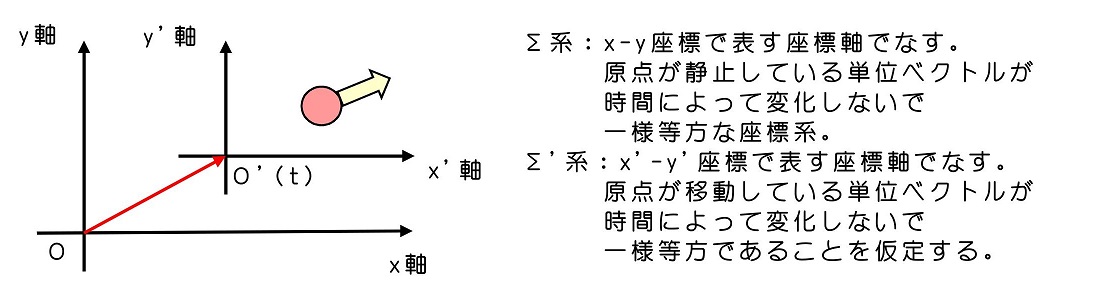
①Σ系に対して静止している物体の座標をΣ'系で表してみる
静止している座標系Σは原点が静止し、単位ベクトルが時間により変化せず、座標も一様等方であるように選択するとしよう。この時、Σ'系の原点O(t)はΣ系の座標を表すベクトルで表すことができる。

さて、Σ'系も原点が移動するだけで単位ベクトルが時間変化せず、座標が一様等方であることを『選択』しよう。ベクトルとは、原点が異なっても平行移動で一致すれば、同じベクトルと考えることができるよ。よってΣ系とΣ'系の単位ベクトルを同一と『選択』しよう。
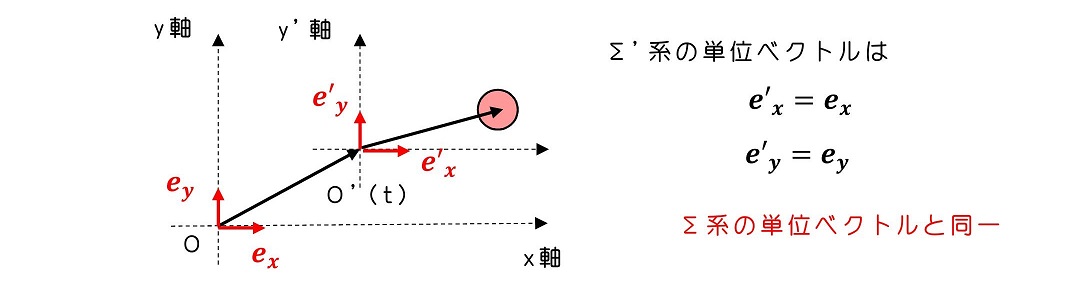
Σ'系での玉の位置をr'(t')と置き、Σ系ではr(t)とすると、それを単位ベクトルと座標値を用いて、それぞれ次のように表せる。
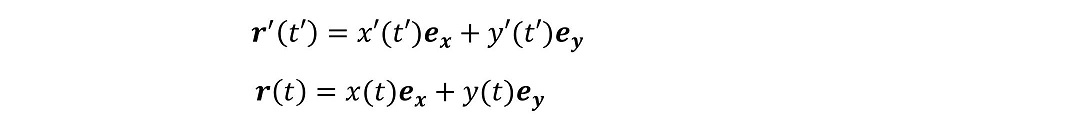
さあ、次はΣ系とΣ'系を関連付けよう。ここで注意すべきは、Σ系の時間の進み方と、Σ'系の時間の進み方はともに一様であるが、その一様さは完全に一致するとは『まだ』していない点である。つまり、Σ系で1秒進んだとしても、現時点ではΣ'系で0.5秒しか進んでおらず、Σ系で2秒進んだとしても、Σ'系で1秒しか進まないという可能性ははらんでいるわけである。
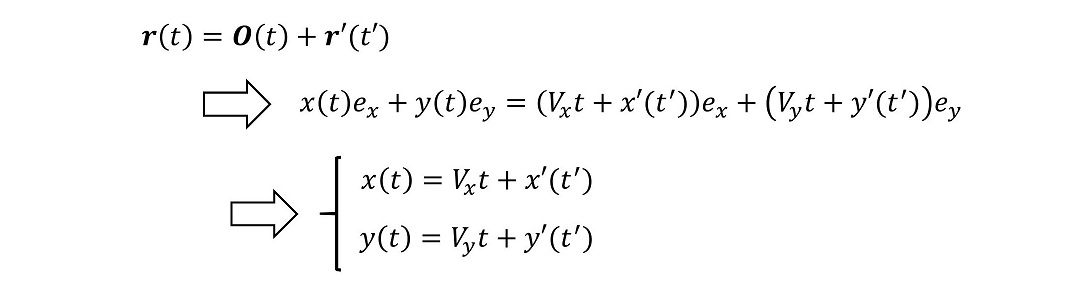
さあここで、tとt'が次の関係にある時のことを考えよう。

今、Σ系に対して静止している物体を考えている。すなわち、Σ系で時間tで微分すると、ゼロになるということである。これを式で表すと次のようになる。
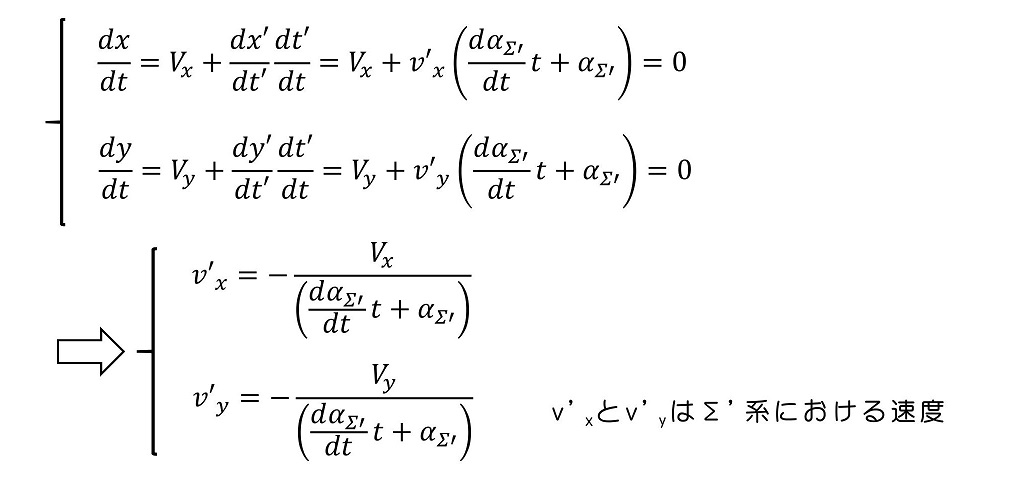
最も単純な方法として、α=1を『選択』することができる。すなわち、動いている系Σ'と、動いていない系Σは同じ時間の進み方をすると仮定するわけである。
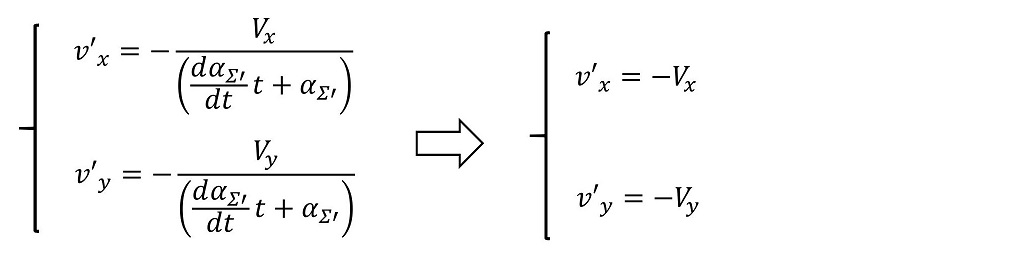
さて、ここまで来て導かれている結果を少し議論しよう。今、Σ系に対して静止していた玉の動きを、Σ系に対してVで動いている系Σ'から見ると、-Vの速度で玉が動いているということになるよ。Σ'系が永遠に等速Vで動くと考えると、Σ'系から見れば玉は等速-Vで動き続けることになるね。
Σ'系で見ると、-Vで動いている玉は、永遠に-Vで動き続けることになるね。これは、慣性の法則を保証しているよ。
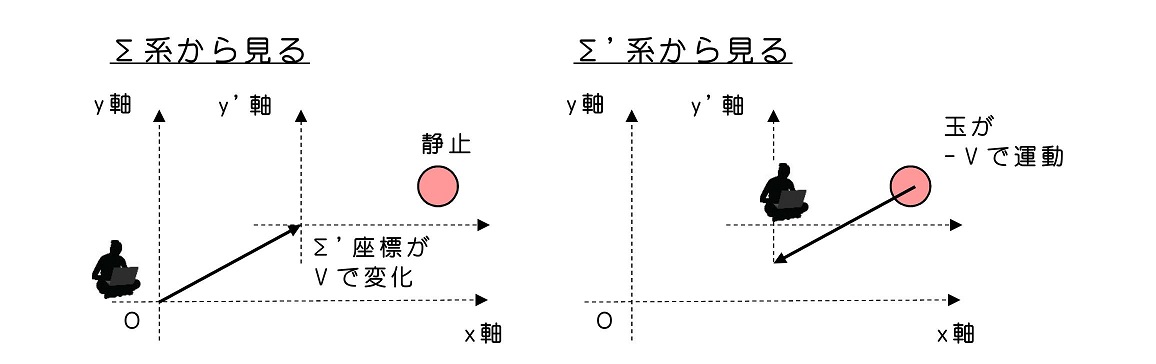
より一般的に、Σ系で速度vで運動している玉が、Σ'での速度v'とどのように関連しているかを示そう。もちろん、この時、今まで前提として選択してきたことを用いるよ。
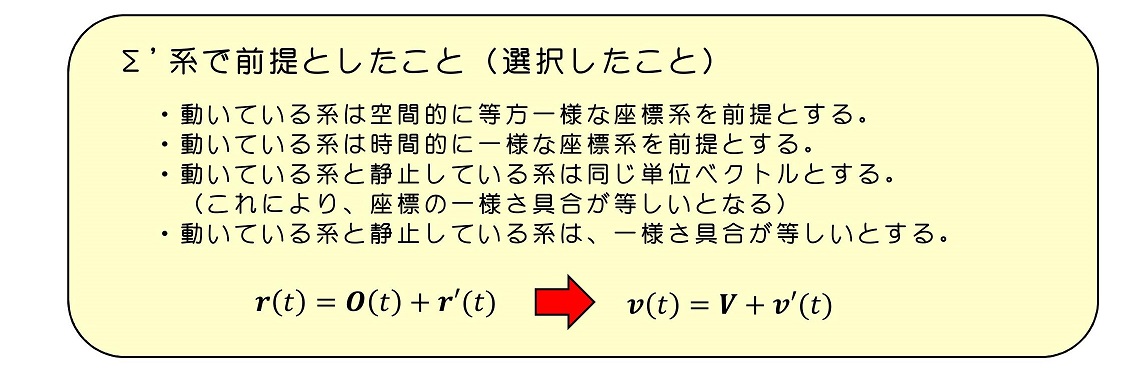
Σ系でVで運動している玉は、Σ'系では速度ゼロで静止しているように見える。よって、Σ'系であったとしても、確かに物体の速度はΣ系とはことなるが、慣性の法則という、静止している物体は静止し続け、動いている物体は等速で動き続けるという法則が成立するよう、座標系を構築(選択)することが可能になるわけである。
②運動の法則は成立するか?
このような座標系のとり方が、ほかの法則でも成立するとき、自分が動いている座標系の上にいるのか、止まっている座標系の上に存在するのかを区別する方法はない。運動方程式をΣ'系に変換してみよう。
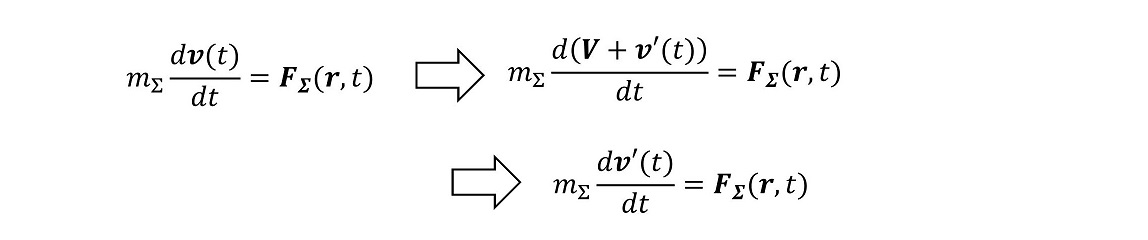
ここで、当然Σ系とΣ'系で時間の進みが等しいことを前提とした。運動方程式を扱う場合、座標以外にも質量と力という2つの要素が入ってくる。そもそも質量とは、力が働いたときにどのように加速度が発生するか、その係数を表している。同じだけの力が働いたときに、動いている座標系と、静止している座標系で、加速の仕方に差が生じるか?を考える。また、この世にはたくさんの力が存在するが、すべて運動している座標系と静止している座標系で違いが出うるのかを考える。
実際に測定をしてみよう。物理学とは、理論のみで構築されるのではなく、現実世界の実験結果によって構築される学問だからである。新幹線に乗っていようと、家の中にいようと、自分の体重に変化はない。その他存在するいろいろな力も運動している座標系と、静止している座標系で『変わらない』。また、その時の加速度も同じ大きさであるため、質量も変わらない。以上より、運動している座標系でも運動の法則は成立すると考えてよい。

③作用・反作用の法則は成立するか
今、働く力の大きさはΣ'系とΣ系で形が変わらない。反作用は必ず運動している座標系でも、作用と大きさが等しく、向きが真逆になると考えても問題はないだろうか?無論、ないと考える。

上記をすべて仮定することで、運動している系と静止している系の区別がつかなくなる。運動の法則や作用・反作用の法則は力や質量の性質について論じている。一方、慣性の法則は座標変換について論じている。この座標変換をガリレイ変換と呼んでいる。

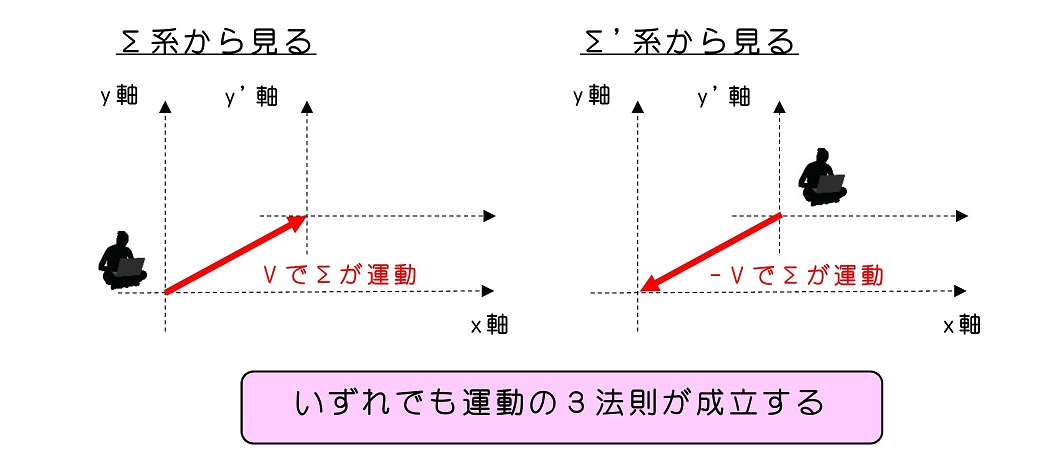
さてここで、運動している系と静止している系が区別つかないように定めた。これは逆にみると、Σ'系が静止しており、Σ系が『-V』で動いている系と考えてもよい。この世には絶対静止している系は存在せず、あくまで相対的であるという考え方をするわけである。どっちが主体かはあくまで相対的なだけである。これを『相対性原理』と呼ぶ。
10.2 重心座標系と実験室座標系
内力のみが働く2体を考えよう。この重心は、必ず等速直線運動する。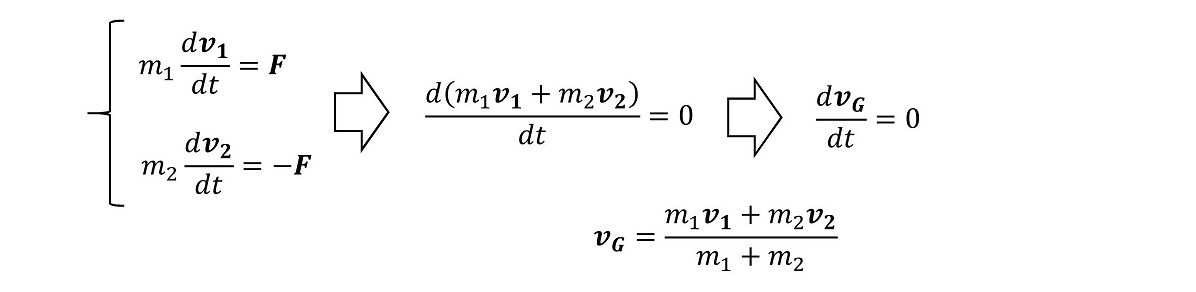
内力のみが働く時、重心の座標を原点ととるような座標系のことを重心座標系と呼び、重心とは関係なく、適当な位置(測定装置の場所などにとることが多い)に原点をとるような座標系のことを実験室座標系と呼ぶ。
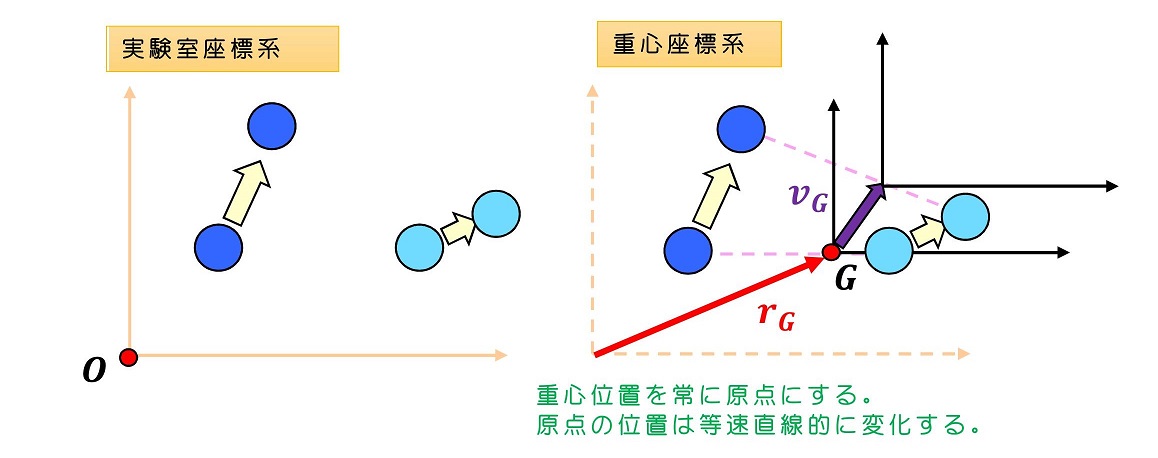
重心座標系では物体の速度はどのように表されるだろうか?
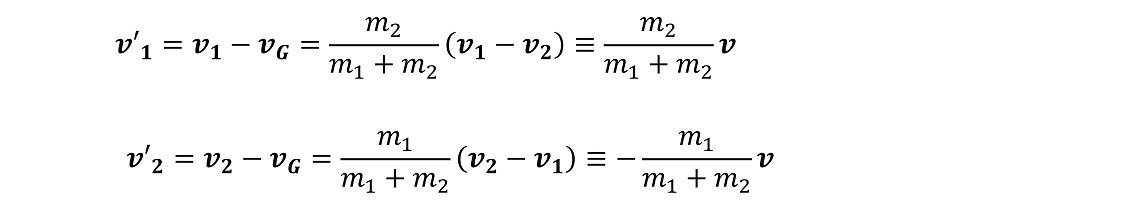
重心座標系で速度を表す場合、きわめて興味深いことがわかる。今、玉2から見た玉1の、実験室座標系での相対速度をvとすると、重心座標系では玉1は相対速度と同じ向きに、玉2は相対速度と逆向き、つまり玉1と逆向きに運動することになる。
またそれぞれの玉の位置は重心座標系ではどのように表されるか?
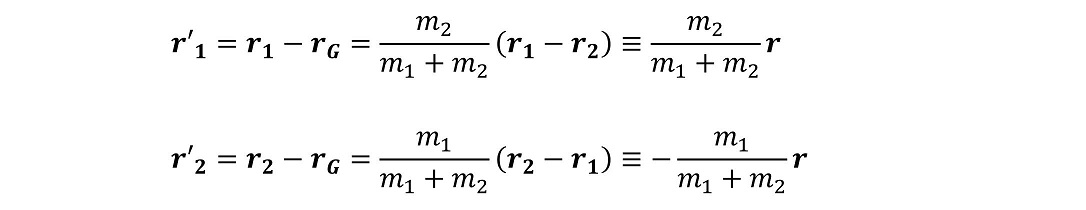
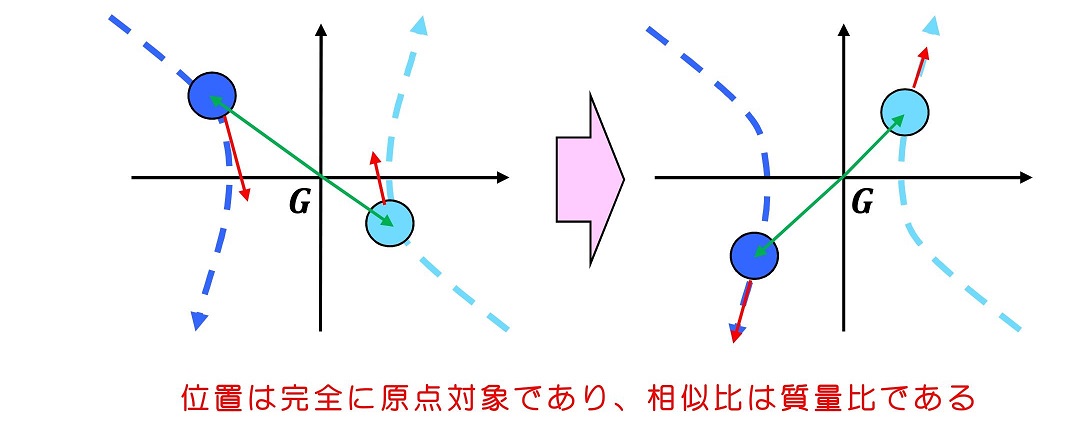
位置座標を表すときも、やはり、玉1と玉2は対照的な位置に存在する。すなわち、内力のみが働く2体の運動を重心座標系で表す場合、その重心座標系でも、運動の3法則が成り立ち、2体の位置は常に原点を挟んだ位置にいて、その速度も常に逆向きであると考えられる。
10.3 完全弾性衝突
内力のみが働く2体の間の完全弾性衝突を扱おう。物体は一般に衝突時に力学的エネルギーが減少する。減少したエネルギーは音(など)として外部に放出されてしまう。いったん外部に放出されたエネルギーは、衝突後、再度物体自身に戻ってくることは極めてまれである。しかし、衝突時に働く力が保存力である場合、力学的エネルギーが一切減少しない衝突と扱えることがある。これを完全弾性衝突と呼ぶ。衝突時には保存するもう一つの物理量が存在する。すなわち運動量である。運動量の保存に必要な条件は、系に内力のみが働くことであった。よって、完全弾性衝突でなければ保存しないわけではない。完全弾性衝突でも、『当然』保存すべき量として扱われるべきである。

重心速度と一致して移動する座標系へのガリレイ変換に伴い、エネルギー保存則および運動量保存則はどのような形に変換されるだろうか?

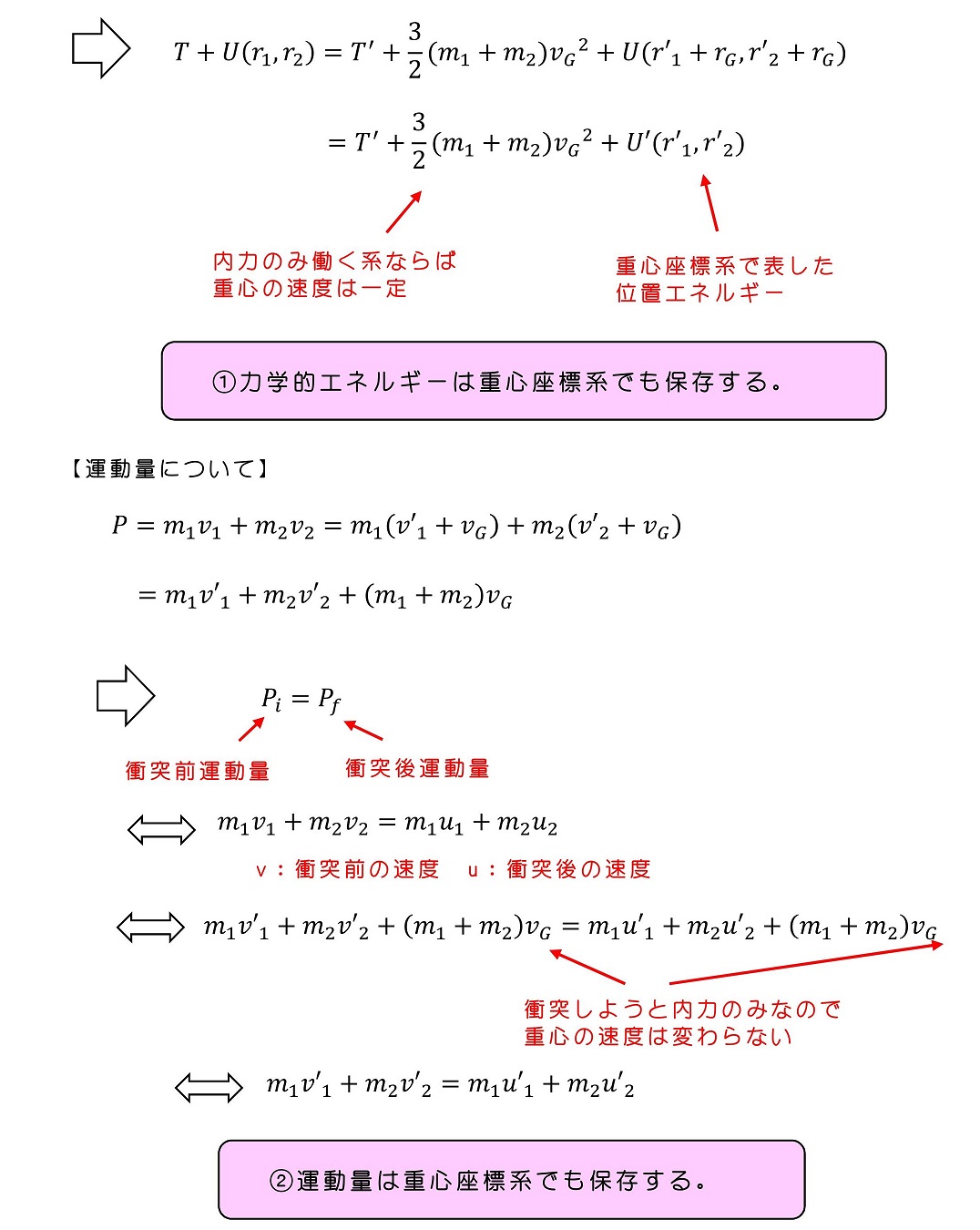
具体的に、衝突の運動について書き下そう。衝突前を、内力による影響が限りなく小さいあるタイミング、衝突後を内力による影響を及ぼしあった後、再度離れていって内力が再び及ばなくなったあるタイミングと定義しよう。この場合、衝突前後で速度はどのようになるか?運動量に着目すると、非常に有意義なことがわかる。

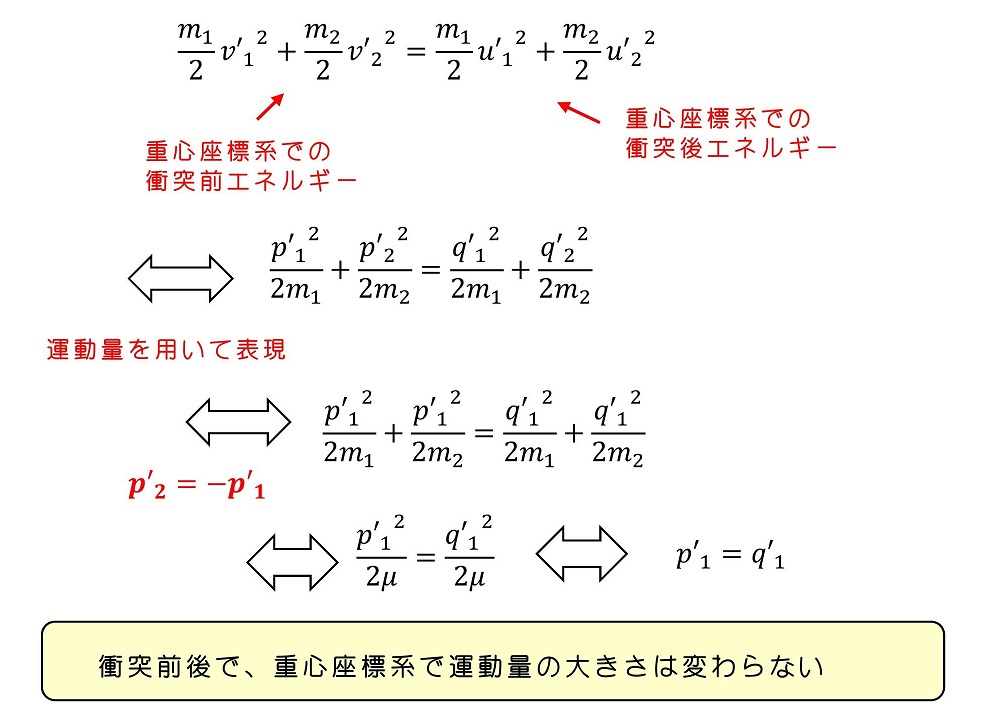
衝突より十分前のタイミングと、十分後のタイミングでは内力が限りなく小さいと考える。すなわち十分前と十分後で位置エネルギーはゼロである。エネルギー保存の法則を運動量を用いて表す。
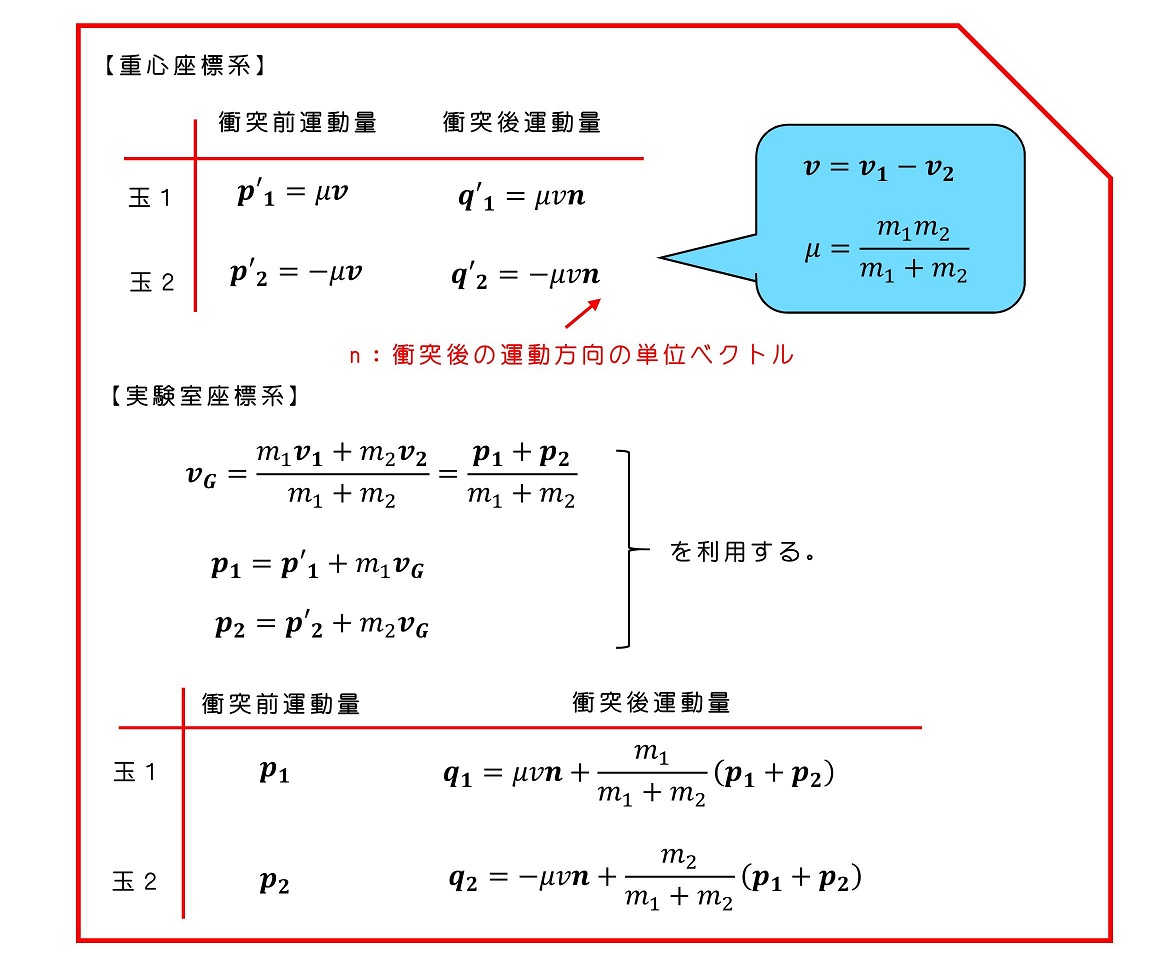
実験室座標系の衝突後の運動量バランスを図示しよう!
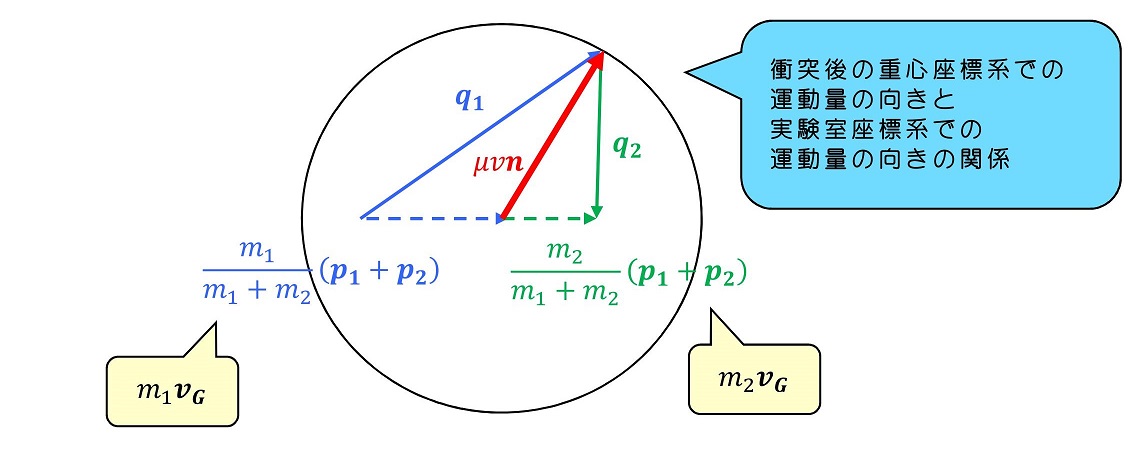
10.4 静止している玉への衝突
衝突の運動をより簡素化し、実験室座標系で静止している玉2に対して、玉1が衝突をする場合を考えよう。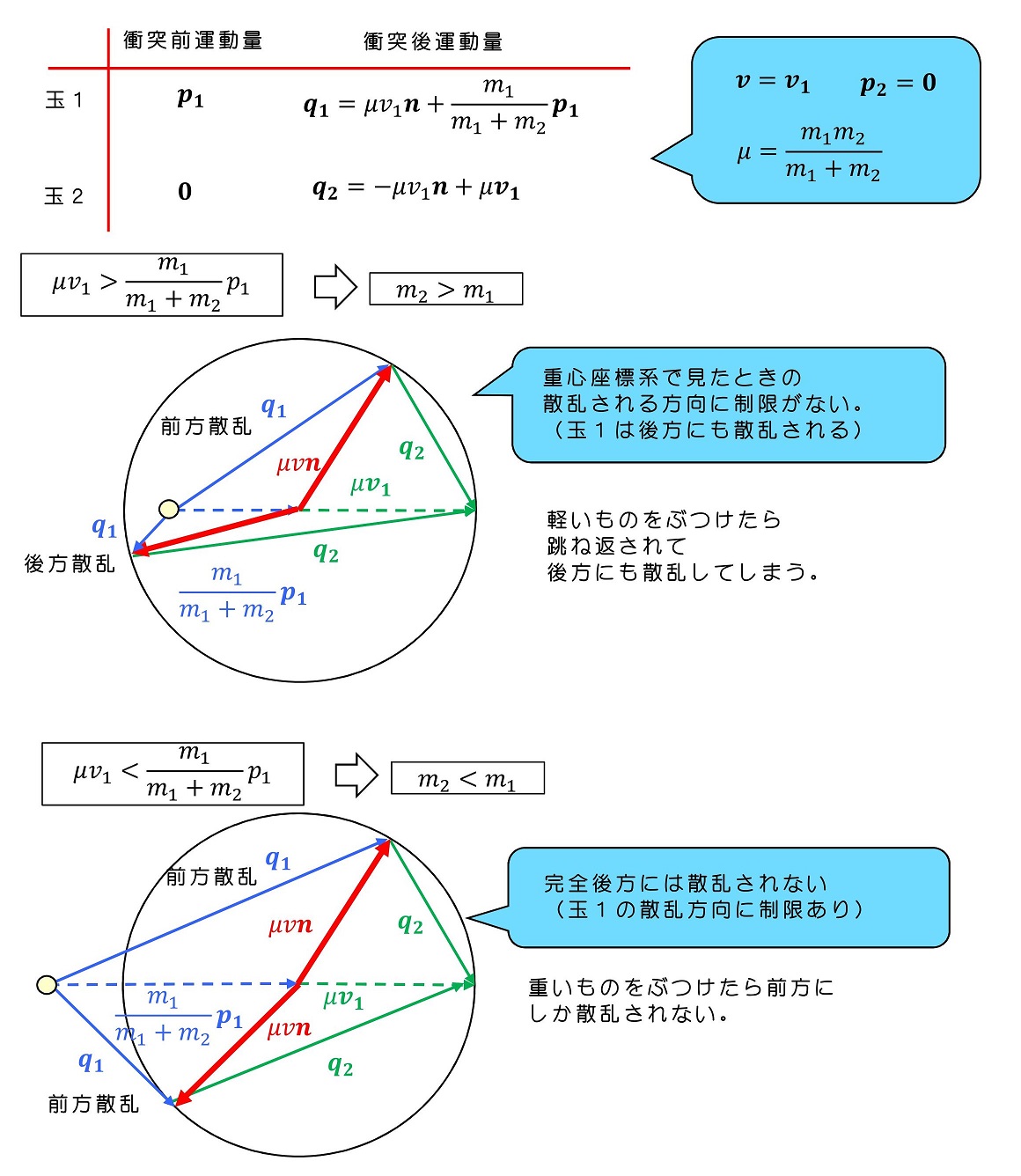
10.5 ラザフォード散乱
有名な問題の一つとして、ラザフォード散乱がある。これを題材にして、散乱問題への理解を深めよう。この世の物質はすべて原子から構成されている。原子は中心に非常に大きな質量をもつ原子核と、その周りを取り巻く非常に軽い電子で構成されている。今、原子核1個に対して電子を打ち込む場合を考えよう。電子はどのように散乱されるだろうか?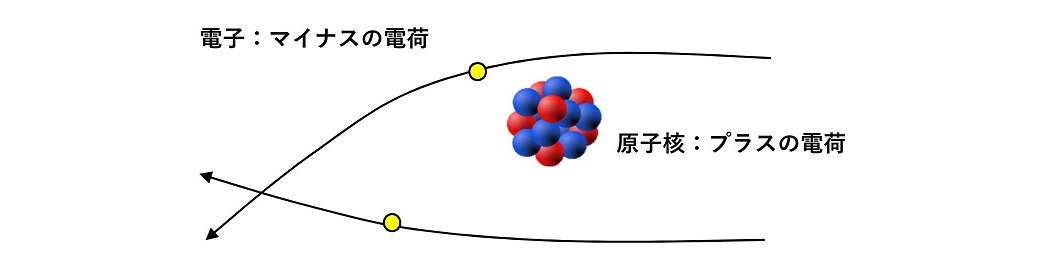
原子核はプラスの電荷をもち、電子はマイナスの電荷をもって互いにひかれあっていると近似してよい。その時両者の間に働く力は重力と同じように2つの距離の2乗に反比例している。引力のため、相対的にひかれあう向きに力を持つ。ここで、電子のほうが原子核よりはるかに軽いため、散乱後の電子は後方にも散乱されうることに注意したい。
実際の電子の運動軌道を計算してみよう。運動方程式を解けばよいが、実はエネルギー保存則と角運動量保存則を用いると運動方程式を解くよりも、より簡易的に軌道を知ることができる。今、重心座標系で考えよう。
重心座標系での角運動量は保存するか?
重心座標系でエネルギーが保存することは導出済みである。角運動量は保存するだろうか?
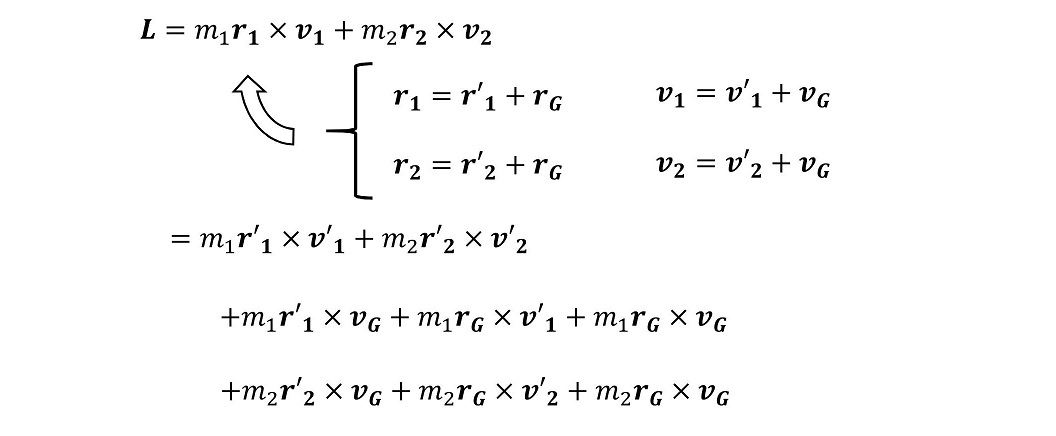
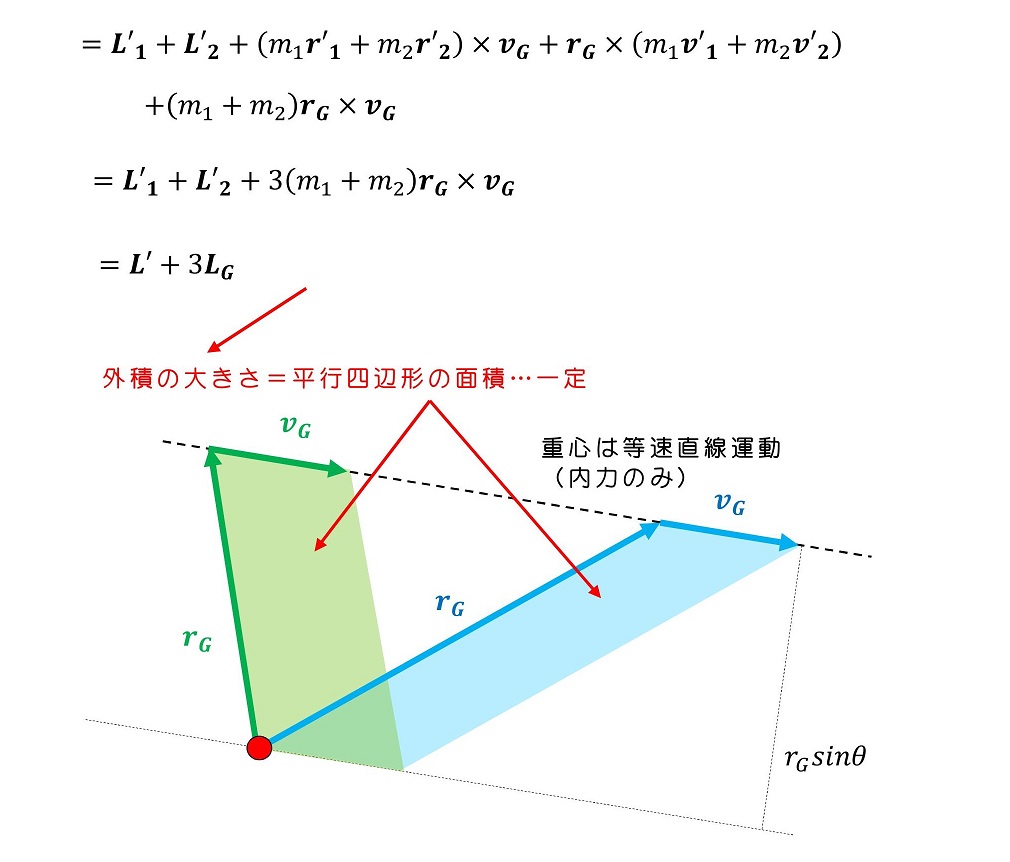
今、内力しか働かない系では、角運動量は保存する。すなわちLは一定である。一方、Lを重心座標系で表すと、重心自身の角運動量LGと重心座標系での角運動量L'の和になる。重心は等速直線運動をするため、その角運動量は一定値である。よって、重心座標系での角運動量L'も保存することが導ける。
重心座標系を用いて、今一度エネルギー保存と角運動量保存を書き下そう。
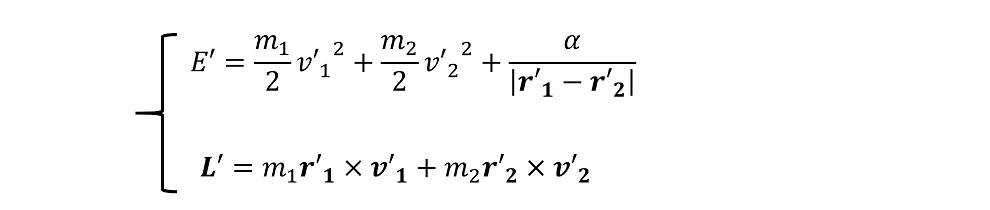
一方重心座標系は、内力を及ぼしあっている2体の相対位置によっても表すことができる。今、粒子2が粒子1に比べて非常に重いと仮定しよう。
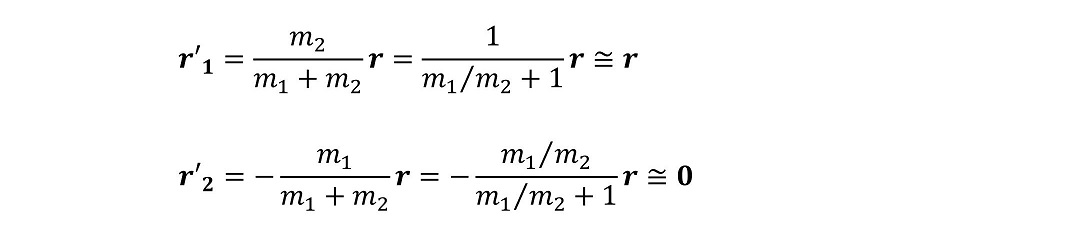
非常に重い粒子の位置はゼロ、すなわち原点に存在するという意味である。これは粒子2が非常に重いため、粒子2の存在位置と重心位置が近似的に一致することを表している。粒子1の位置は、粒子1からの相対距離、すなわち原点からみた位置で表せる。これを用いてエネルギー保存と角運動量保存を書き換えよう。
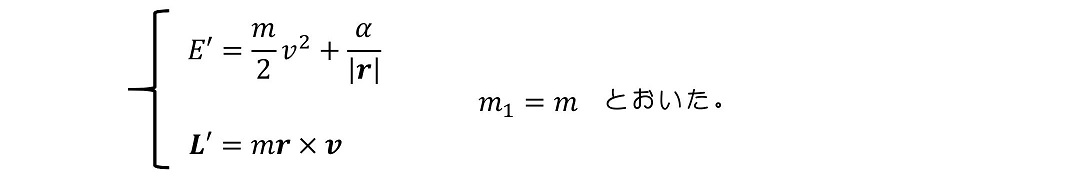
通常『散乱』とは、どの『方向』に飛んで行ったかが重要になる。方向を表すにはx-y直交座標よりもr-θ極座標のほうが便利である。重心座標系におけるエネルギー保存則と角運動量保存則を極座標で表そう。
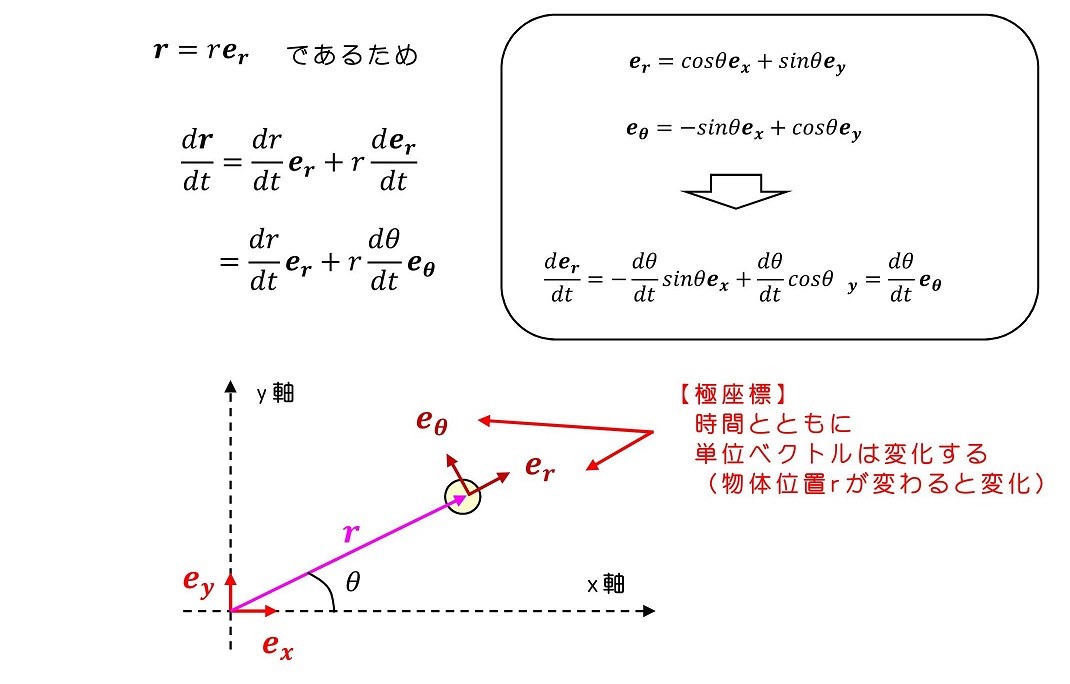
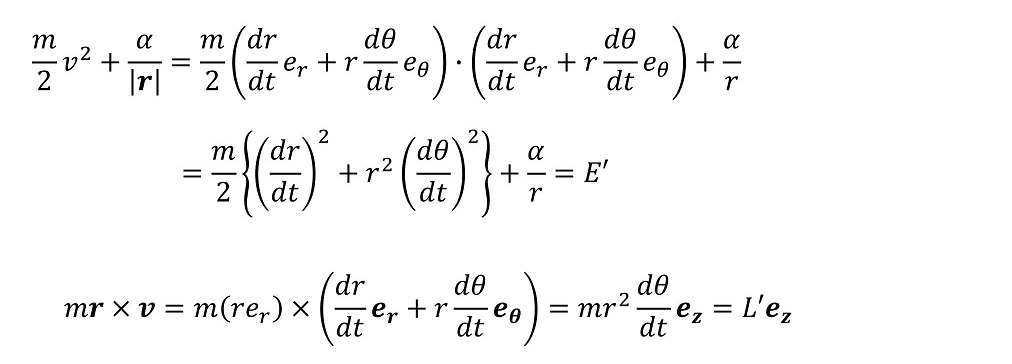
この2つの式を連立させることによって、rとθの関係式を導くことができる。角運動量保存の法則の式を変形し、エネルギー保存の式に代入する。

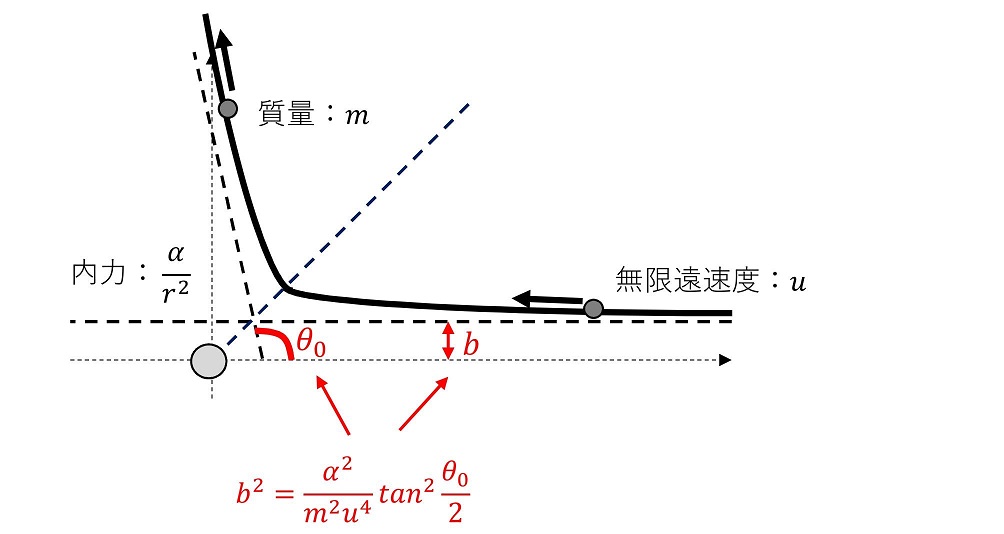
今、軌道を限定しよう。無限遠方(x軸正方向)から粒子がやってきて、原点に存在する粒子に散乱された結果、x軸からθ0の方向に飛んで行ったと考えよう。
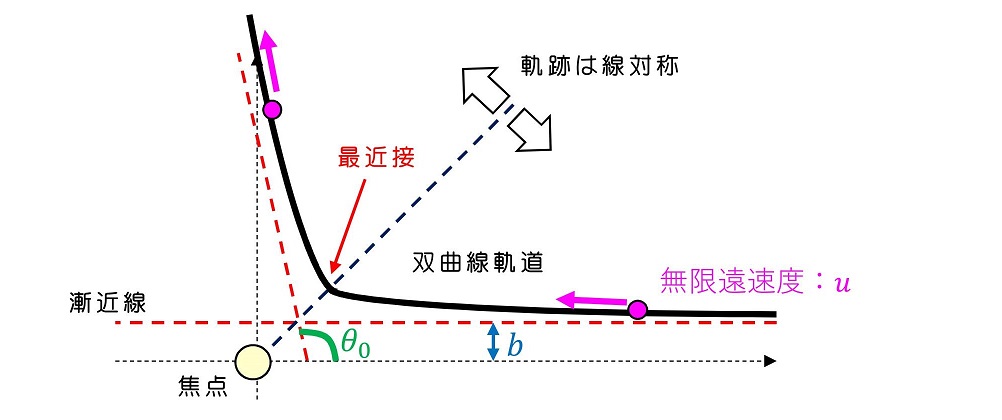
さて、内力が距離の2乗に反比例する場合、その軌道は『楕円』『放物線』『双曲線』のいずれかになることはすでに調査した。(古典力学-9参照)無限遠から近づいた粒子がθ0の方向に散乱されるという運動の条件を加えると、軌道は『放物線』か『双曲線』のいずれかになる。どちらも焦点から最近接位置に引いた直線に対して、線対称軌道になる。
この事実を用いて積分を実施しよう。dθの式が±両方存在しているが、これは近づいてくるときと遠ざかるとき両方を表しているためである。近づくとき、θが増えるとrは小さくなる(マイナス)が、最近接点を越えて遠ざかるときにはθが増えるとrは大きくなる(プラス)。積分を散乱前の無限遠から、散乱後の無限遠まで実施しよう。軌道が最近接点で対称であるため、積分は次のようになる。
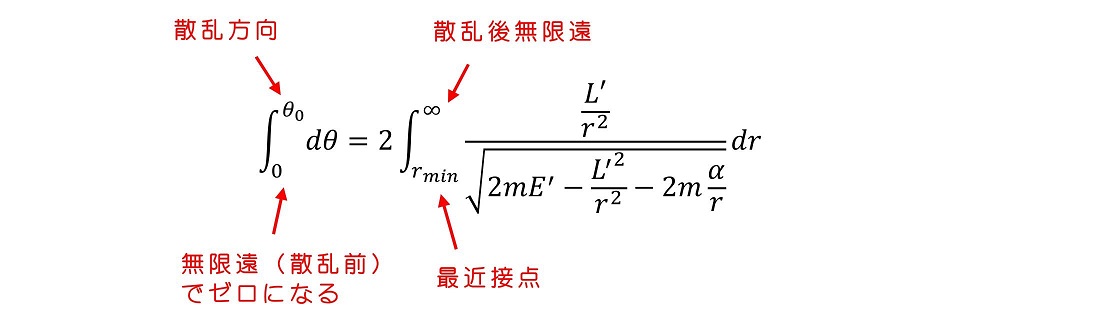
さらに、無限遠での速度や位置を用いてエネルギーと角運動量(E'とL')を定めて式を簡略化しよう。
【エネルギー】
無限遠では位置エネルギーがゼロであるため

【角運動量】
無限遠のため、rが無限に大きくなるが、同時にθは無限に小さくなる。原点に粒子が近づいてきた時、角運動量は明らかに有限の値を持っている。角運動量は保存するため、無限遠でもある値に収束するはずである。

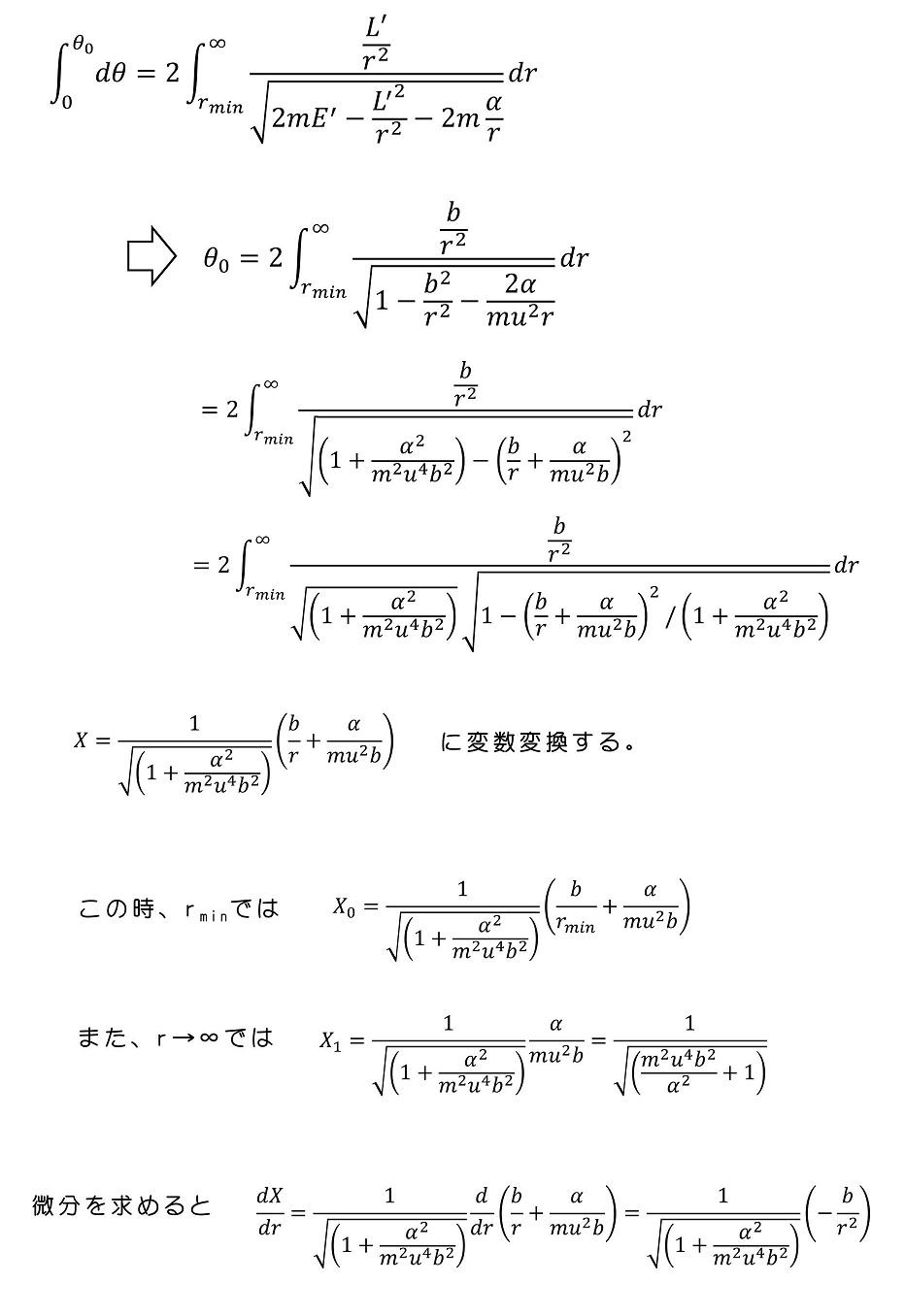
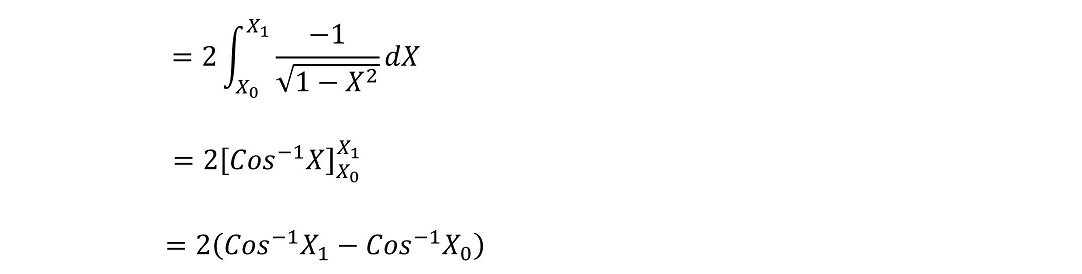
rminを求めよう!
rminを求めることで、X0を具体的な形で与えることが可能である。最近接点の原点からの距離をどのように求めればよいか?最近接の瞬間では、r方向に動いていない(動径方向に直角にしか動いていない)ことがわかる。エネルギー保存則を用いよう。

ここで下記計算を行う。
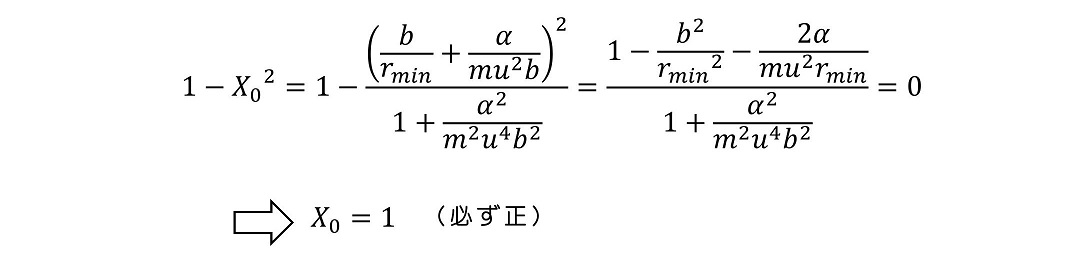
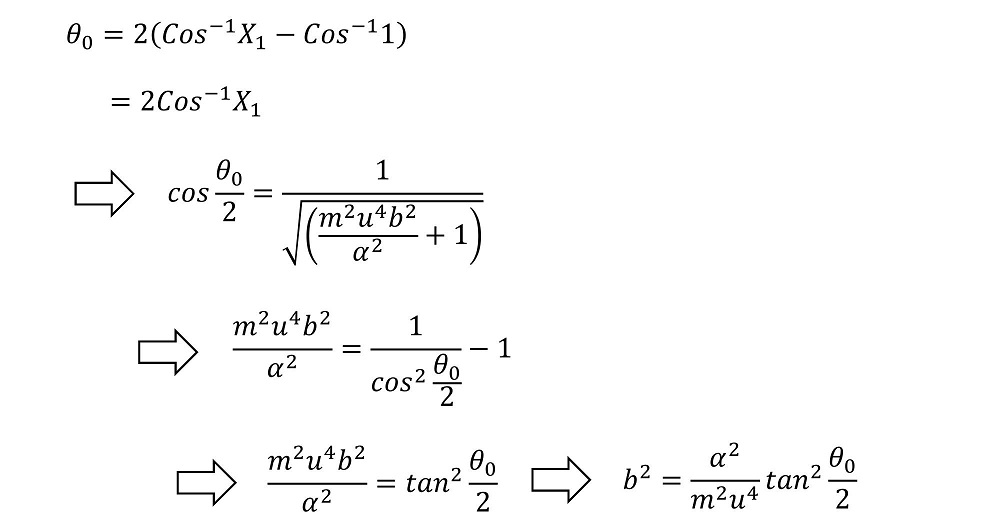
これで求めることができたのはどのような事実であろうか?質量m、内力の大きさを表す係数α、無限遠での初速uに対して、粒子からbオフセットした位置から粒子を入射すると、θの角度に散乱されるという関係式が求まったわけである。
10.6 散乱断面積
散乱問題を扱うときに非常に重要になる、散乱断面積を求めよう。散乱断面積とは何か?端的に言ってしまえば、入射粒子を散乱させる、実効面積のことである。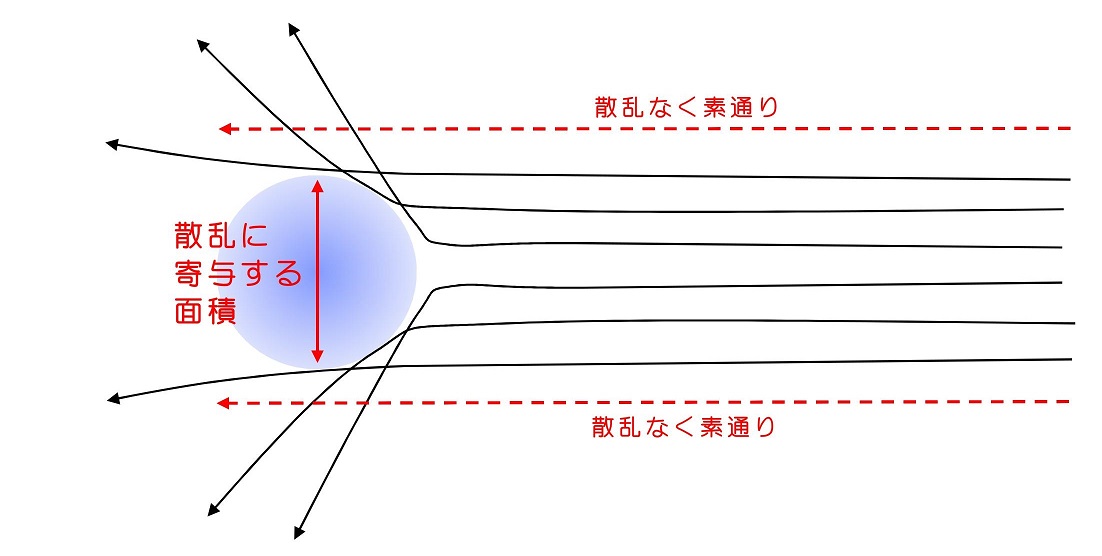
もし、ビリヤードの玉のように、有限の大きさを持っている物体なら、散乱断面積は明らかにビリヤードの玉の正面からみた面積である。ただ、原子核による電子の散乱を考えるときは、困難である。原子核と電子の間のクーロン力と呼ばれる電荷の間に働く力が、散乱を引き起こす原因であり、原子核を正面から見た面積の外部に電子が突入しても、電子はクーロン力を受けて散乱されるからである。では、より一般的に、散乱断面積はどのように定義すればよいか?
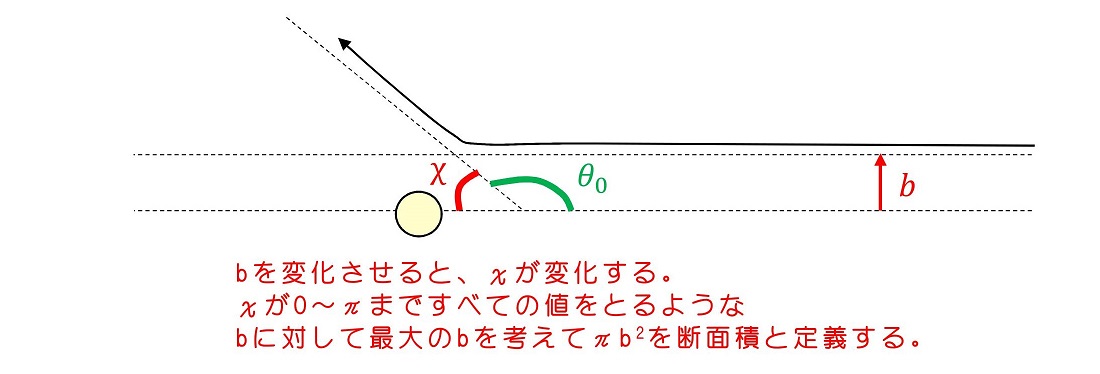
とはいえ、いきなりbの最大値を求めるのが困難であったり、一般に拡張するのが難しいため、次のように定めることが多い。
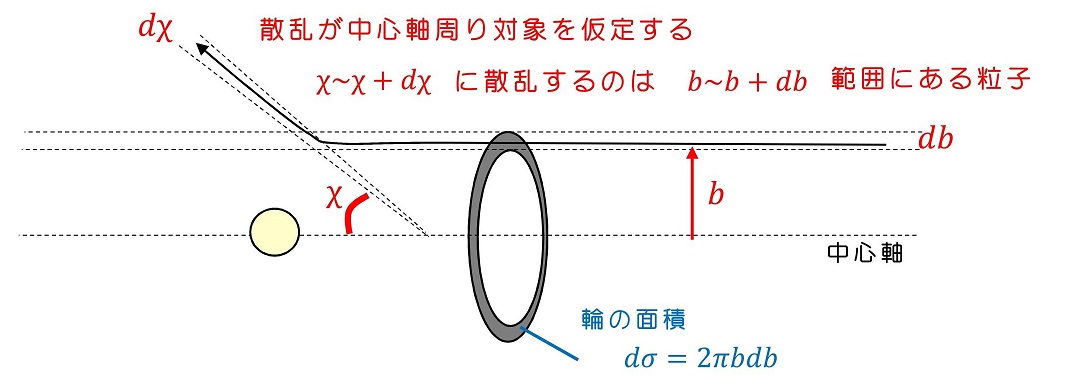
今、中心軸からの離れbと散乱角χが単写像で関連づけられているとする。この時、db/dχを通して、面積とχが関係づけられる。
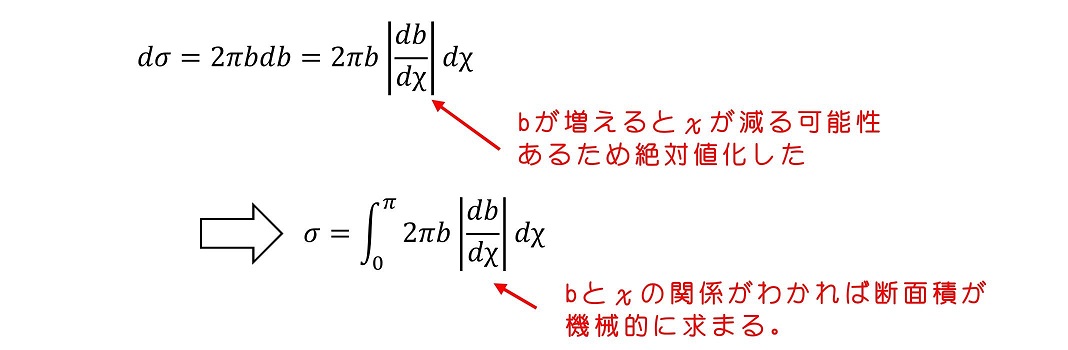
ラザフォード散乱に導入しよう
試しに求めてみよう。ただし、現在はθ0とbの関係しか求めていないため、χとbの関係式に焼き直す必要がある。
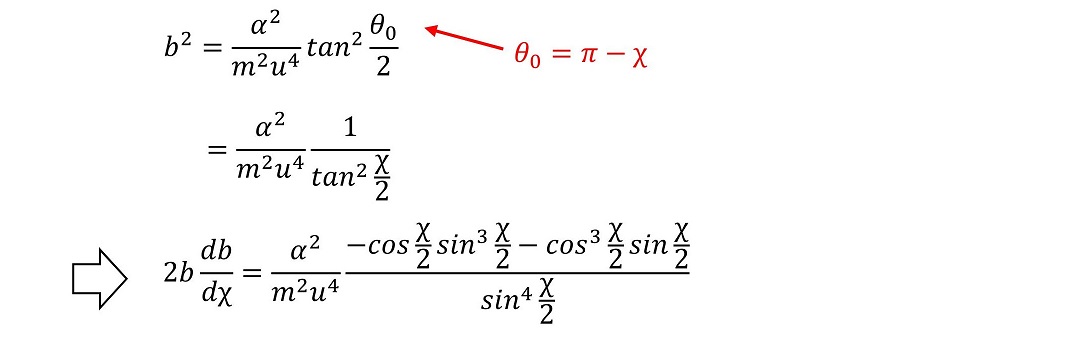
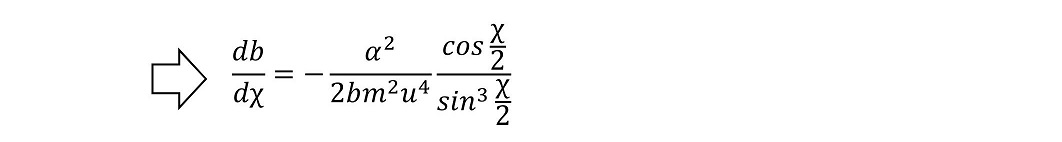
これを散乱断面積の微分方程式に代入する。