11.1 慣性力とは
今、ある座標系が存在し、運動の3法則が成立しているとする。この座標系原点に対して、等速で動く新しい原点を持つ座標系を考えても、同じように運動の3法則が成立するよう、座標系を選ぶことができる。我々は次に、加速度運動をする新しい原点をもつ座標系の性質も考えたい。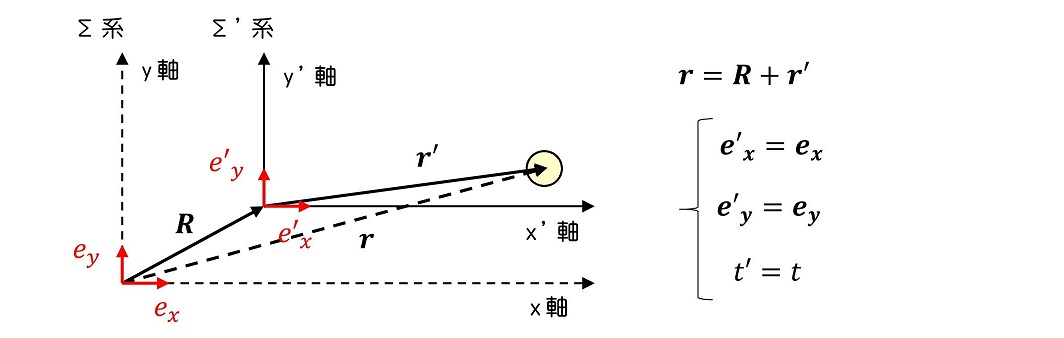
等速運動する系を考えたときと同様に、加速度運動をするΣ'系も空間は等方的かつ一様(単位ベクトルがΣ系と同じ)であり、時間の進みも一様(tとt'が同じ)であると仮定しよう。Σ'系での運動方程式を考えてみよう。
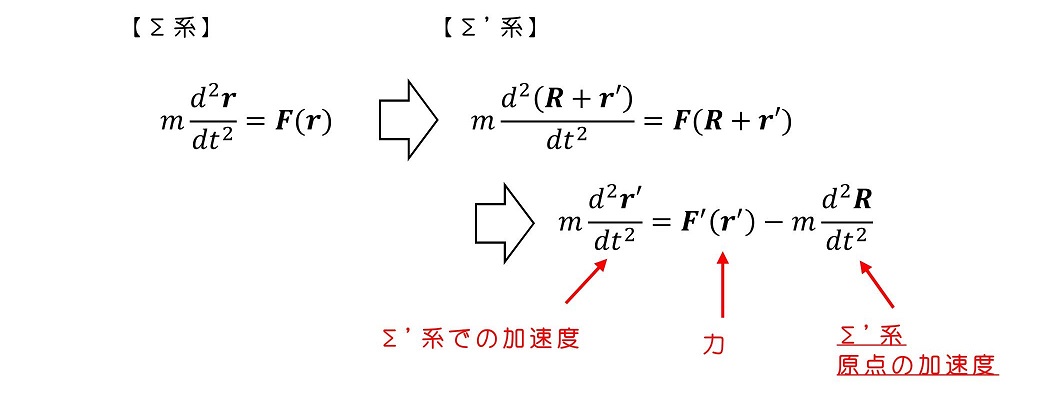
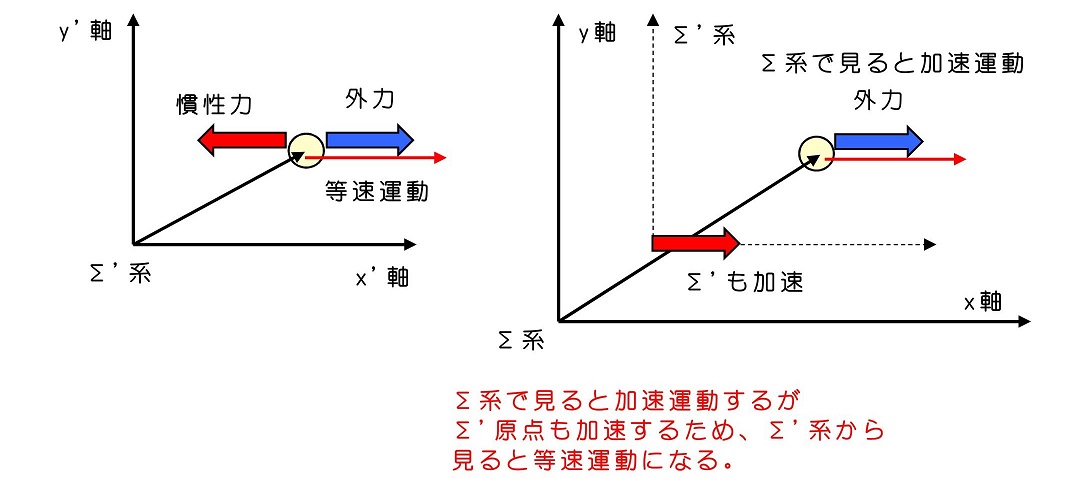
Σ'系の原点が等速運動をしているとき、原点の加速度はゼロであるため、運動方程式はΣ系のものと変わりないと扱えるだろう。だが、もし加速度運動をしているとき、その効果が通常の力からマイナス側に作用する。これを『慣性力』と呼ぶ。
慣性力含めて、働く力と考えれば、Σ'系でもニュートンの運動の法則が成立する。では、運動3法則のうち、ほかの2つはどうだろうか?

Σ'系では、すでに慣性力が働いている。すなわち、それを打ち消すような力が働いていると、実質的に力が働いていないのと同値になる。この時、加速度がゼロであるため、物質はΣ'系から見ると、必ず等速運動していることになる。しかし注意しなければならない。Σ系から見ると、力が働いているため、加速度運動になる。
作用反作用の法則がΣ'系でも成立するか?事実として、加速度運動している系内においても、作用反作用の法則は成立する。詳細は割愛する。
11.2 等加速度直線運動する座標での慣性力について
最も単純な慣性力は、Σ'座標系の原点が等加速度直線的に動いている場合である。ちょうど、駅から出発した直後の電車の中にいる場合をイメージすればよい。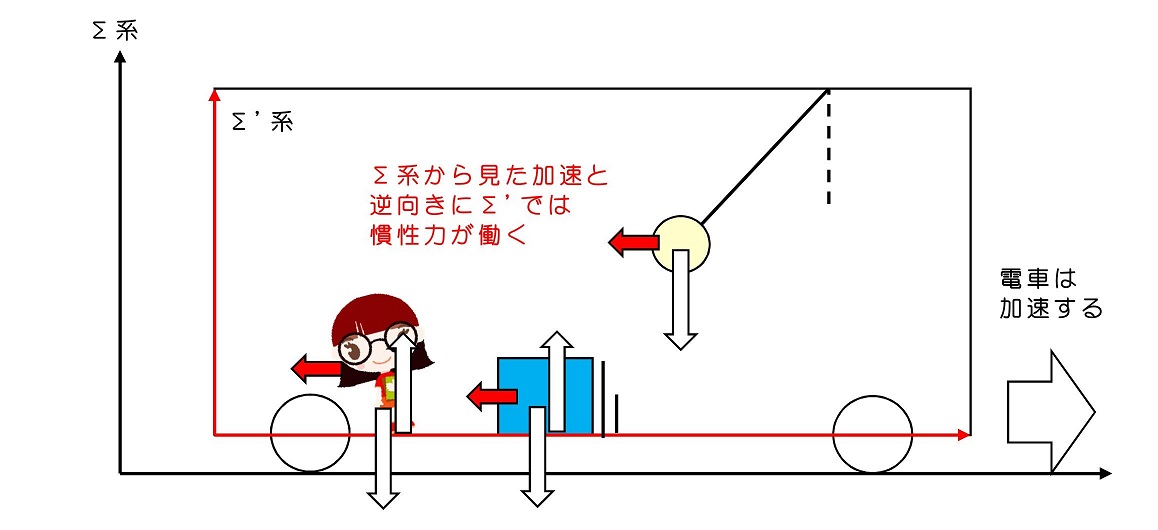
鉛直方向は重力や垂直抗力であり、Σ系であったとしても同じように働く力である。水平方向に働く力が慣性力である。加速している最中の電車の中では、すべての物体が加速と逆方向に引っ張られるように、力が働くように感じる。この力はあくまでΣ'系で記述するときに働くとみなすものであり、Σ系では働く力ではない。地面に置かれた箱は後ろに滑り、天井からつりさげられた玉は斜めに傾く。
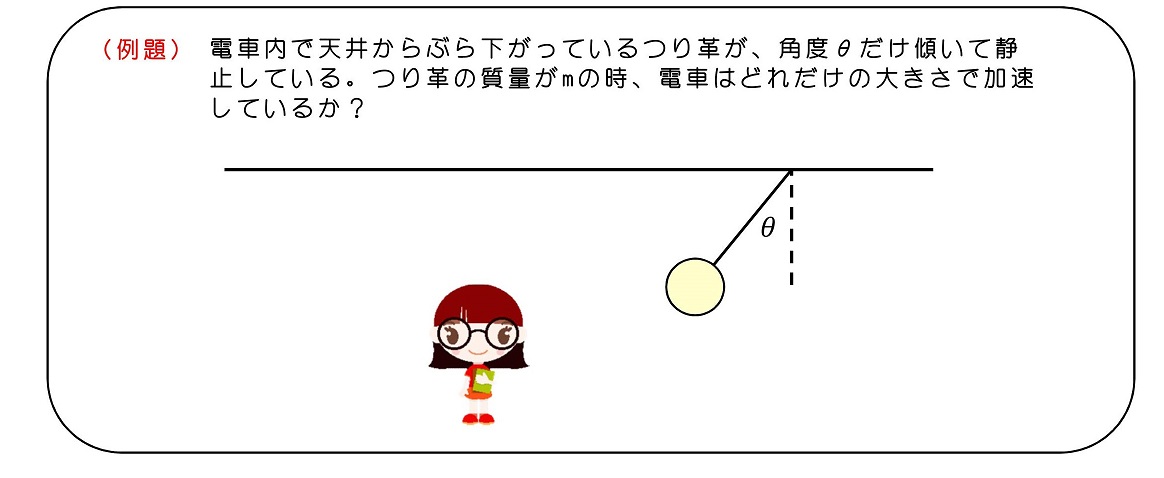
自分は電車に乗っているのか、いないのか、外の景色の移りかわりを見ない限り、基本的にはわからない。だが天井から釣り下がっているつり革が、重力以外の力を受けて斜めになっていることで、少なくとも加速度系に自分がいるってことを、予想することができる。
運動を予想しよう
つり革は重力によって基本的には下に垂れ下がるが、斜めに傾くということは横方向に力が働いたということである。外部から見て電車が加速する向きと、内部から見た慣性力は向きが逆である。今、左方向につり革が振れたということは、電車は右方向に加速していると予想できる。
軸を決め、力を整理する
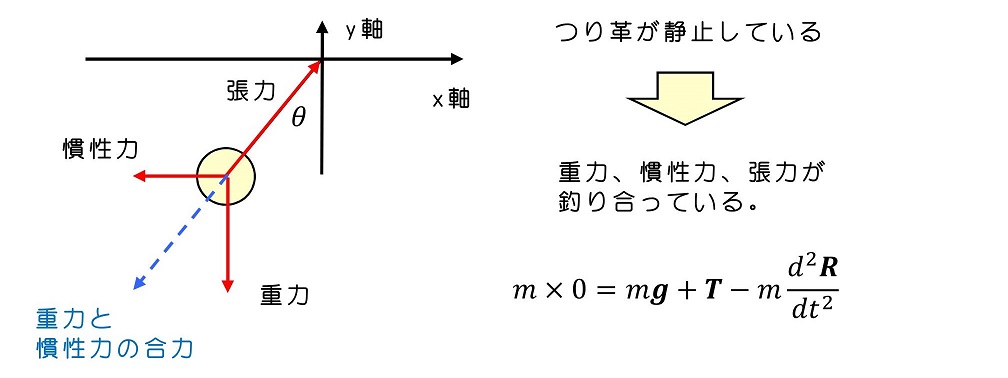
式をたて、答えを求める
慣性力と重力の合力を考え、この力と張力が釣り合っているはずである。幾何的な考察より、答えを求めることができる。慣性力は質量×電車の加速度で表すことができる。
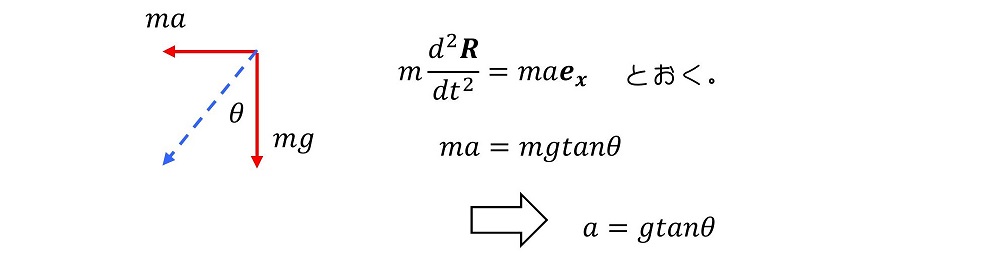
11.3 平面的に運動をする座標系での慣性力
原点が等加速度直線的に動いているΣ'系を考えたわけだが、もう少し一般化して原点が2次元平面上を任意に動いている場合を考えよう。この時、極座標表示を用いると、いくつかの興味深い慣性力が現れる。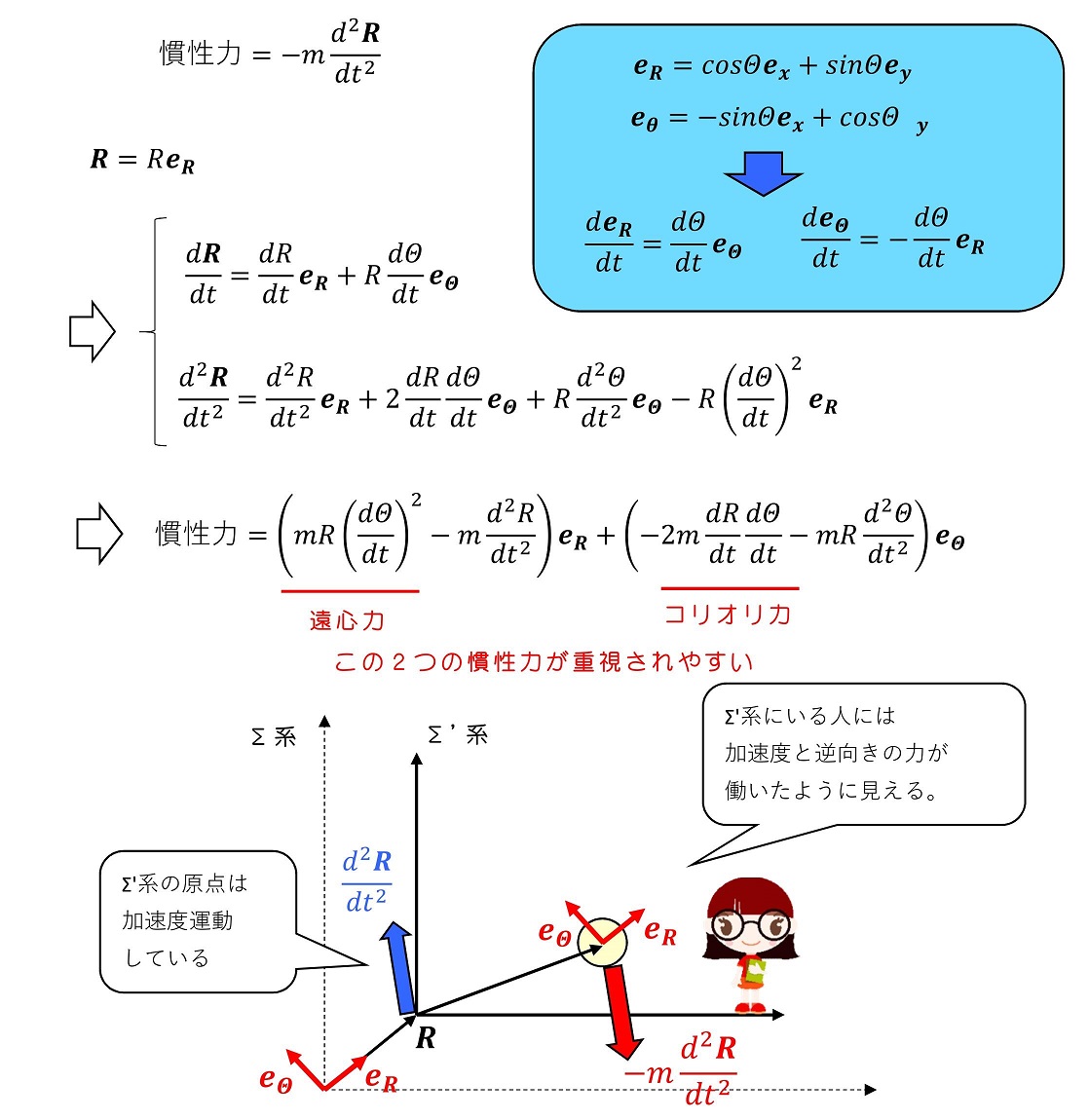
慣性力をeRとeΘ成分で分離しよう。遠心力とコリオリ力が特に重視されやすいため、その2つを開設する。注意すべきは、eRとeΘはΣ'系での物体の位置を表す極座標での単位ベクトルでは『なく』Σ'座標系の原点をΣ系で表したときの極座標での単位ベクトルである。
11.4 遠心力について
今、ひもに結ばれて円運動している玉の動きを記述しよう。回転中心に原点をとったΣ系に対して、運動する玉の中心に原点をとったΣ'で運動を記述するとどうなるか?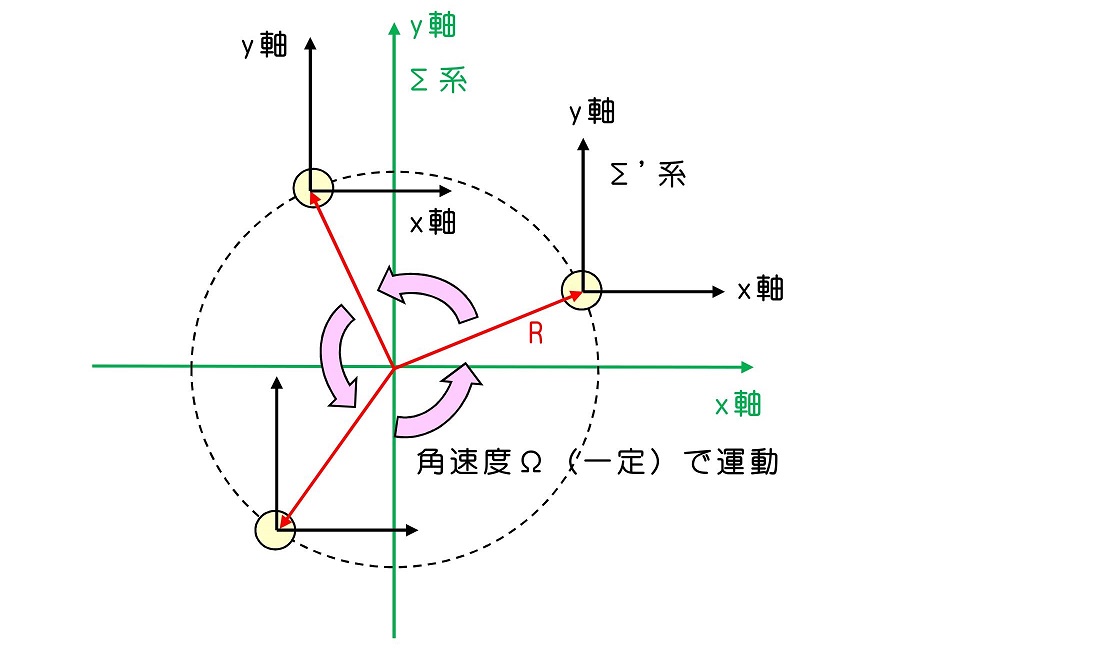
Σ系で記述する場合
今、ひもに結ばれて円運動している玉の動きを記述しよう。回転中心に原点をとったΣ系に対して、運動する玉の中心に原点をとったΣ'で運動を記述するとどうなるか?
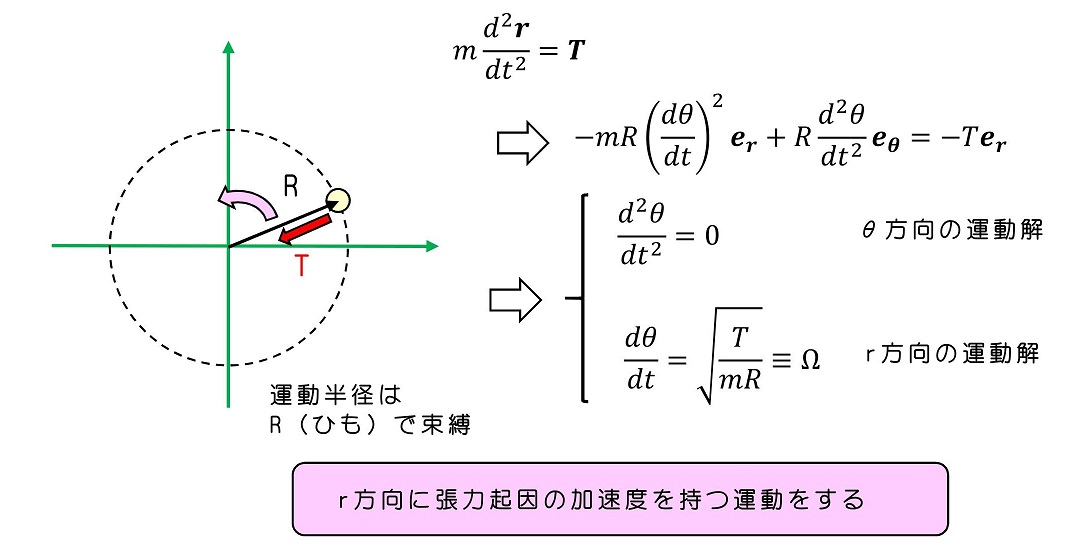
Σ'系で記述する場合
Σ'系の原点は常にΣ系原点の向きに加速するような動きをする。すなわち、Σ'系ではΣ系原点向きとは逆向きに慣性力を持つことになる。張力も玉には働き、最終的には、Σ'系の原点で静止することになる。
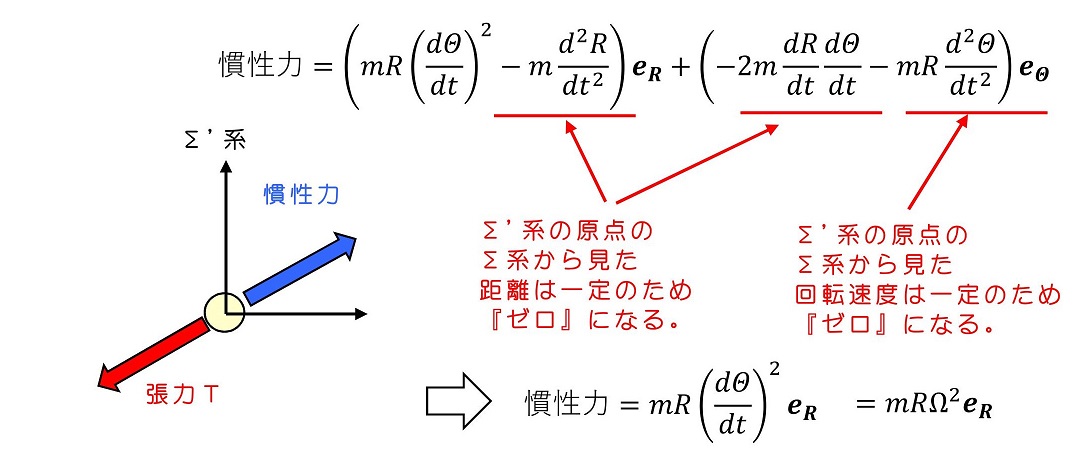
回転運動する座標系に存在している物体は、外向きに吹き飛ばされるような力が働く。これが遠心力の直感的な理解である。
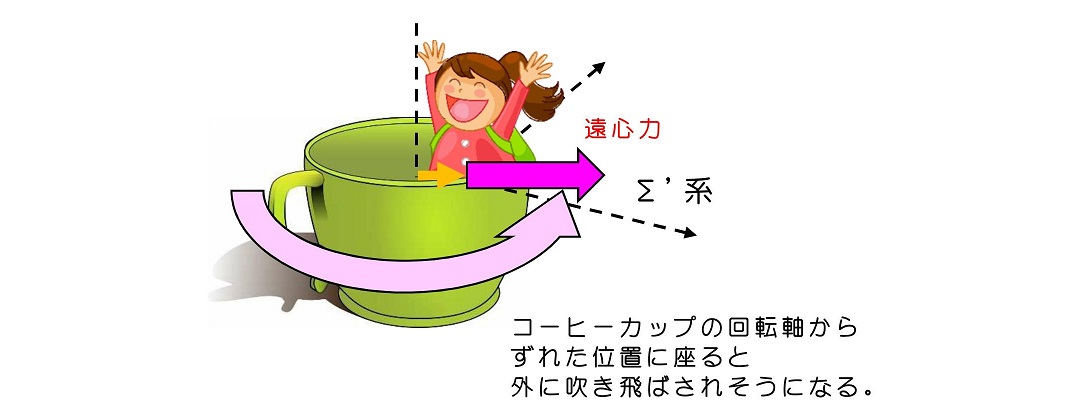
11.5 コリオリ力について
遠心力がΣ系原点から『常に等距離』で『回転する』物体でも働く慣性力なのに対し、コリオリ力はΣ系原点からの『距離が変化』しながら『回転運動』する物体でなければ働かない慣性力である。わかりやすくΣ系原点からの距離変化と原点周りの回転変化がともに等速で行われる運動を考えよう。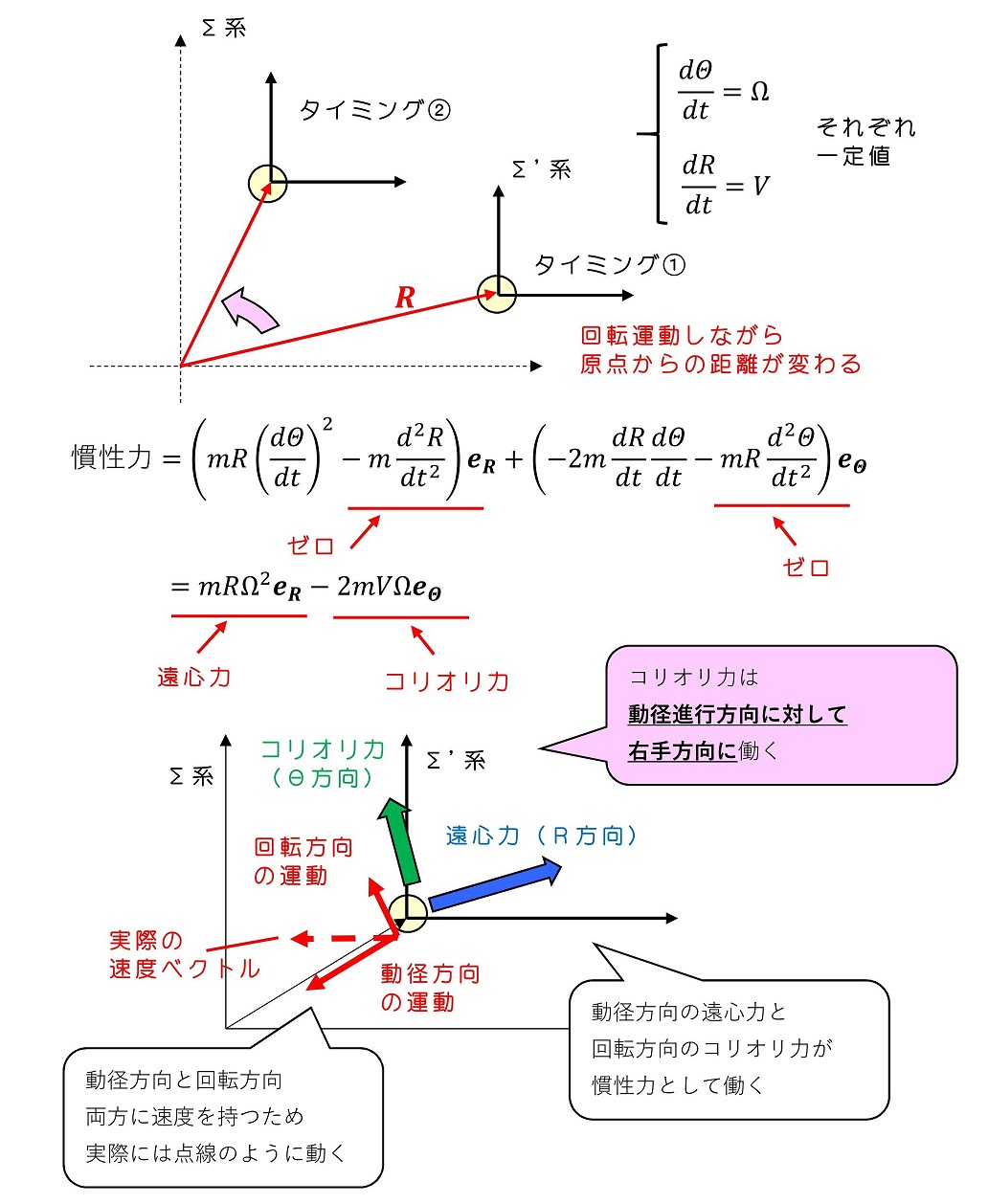
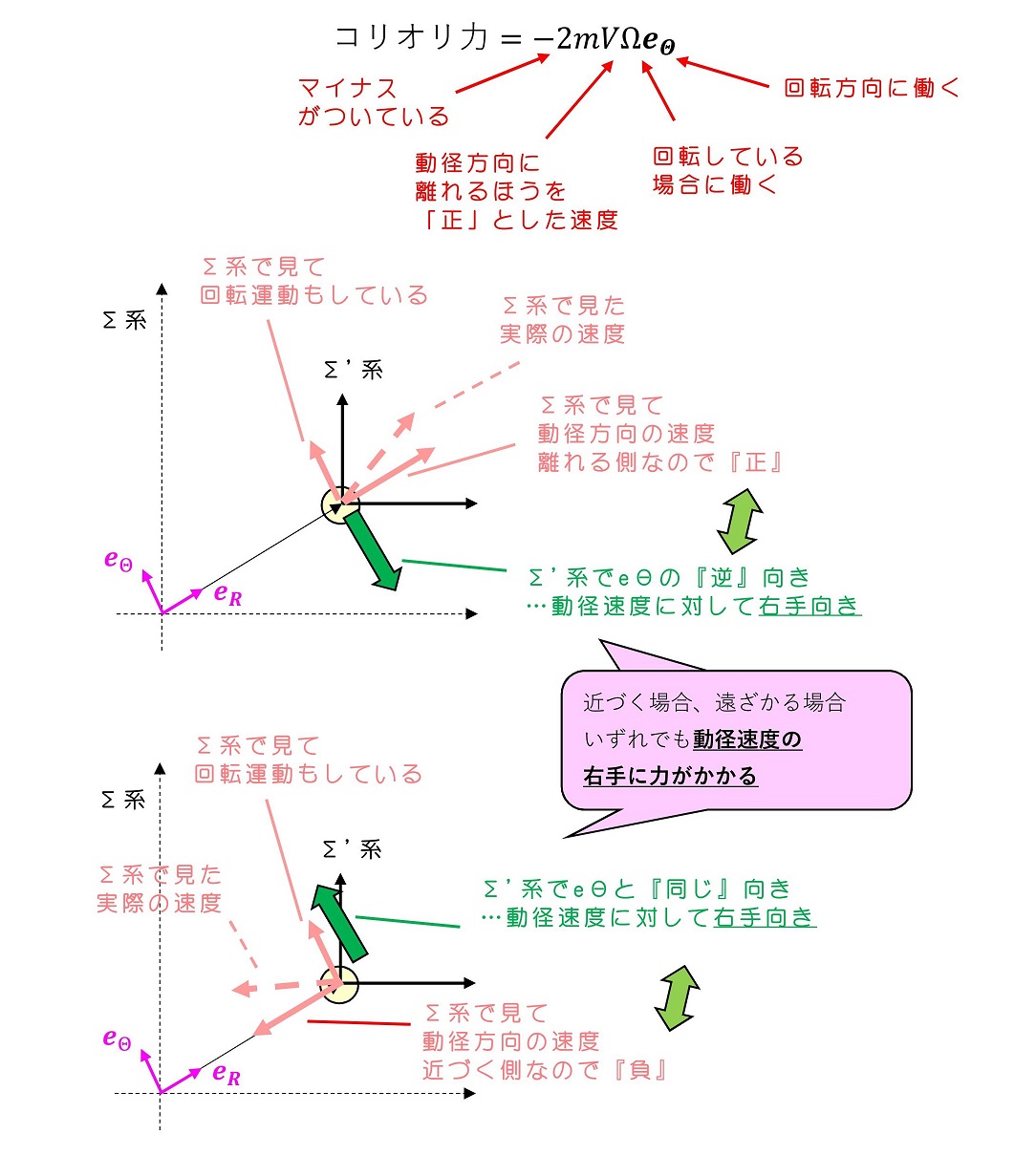
遠心力が外に吹き飛ばされる力であるのに対して、コリオリ力はかなり難しいね。(動径方向に動いているのに対して、右手に働く力となる)コリオリ力についてもう少し詳細を見ていこう。
式を理解しよう
まずはコリオリ力の特徴的な式について理解しよう。何がわかるだろうか。
コリオリ力を直感的な理解とつなげよう
コリオリ力なんて本当に働くか、実感のない人のほうが多いだろうね。実はかなりの速度で回転していたとしても、現実的に働く力は微小であり、銃弾が1km先で数センチ右にずれる程度の力の大きさしか働かないから、身の回りで感じることが少ないんだね。とはいえよく考えると、コリオリの力を直感的に理解できるよ。
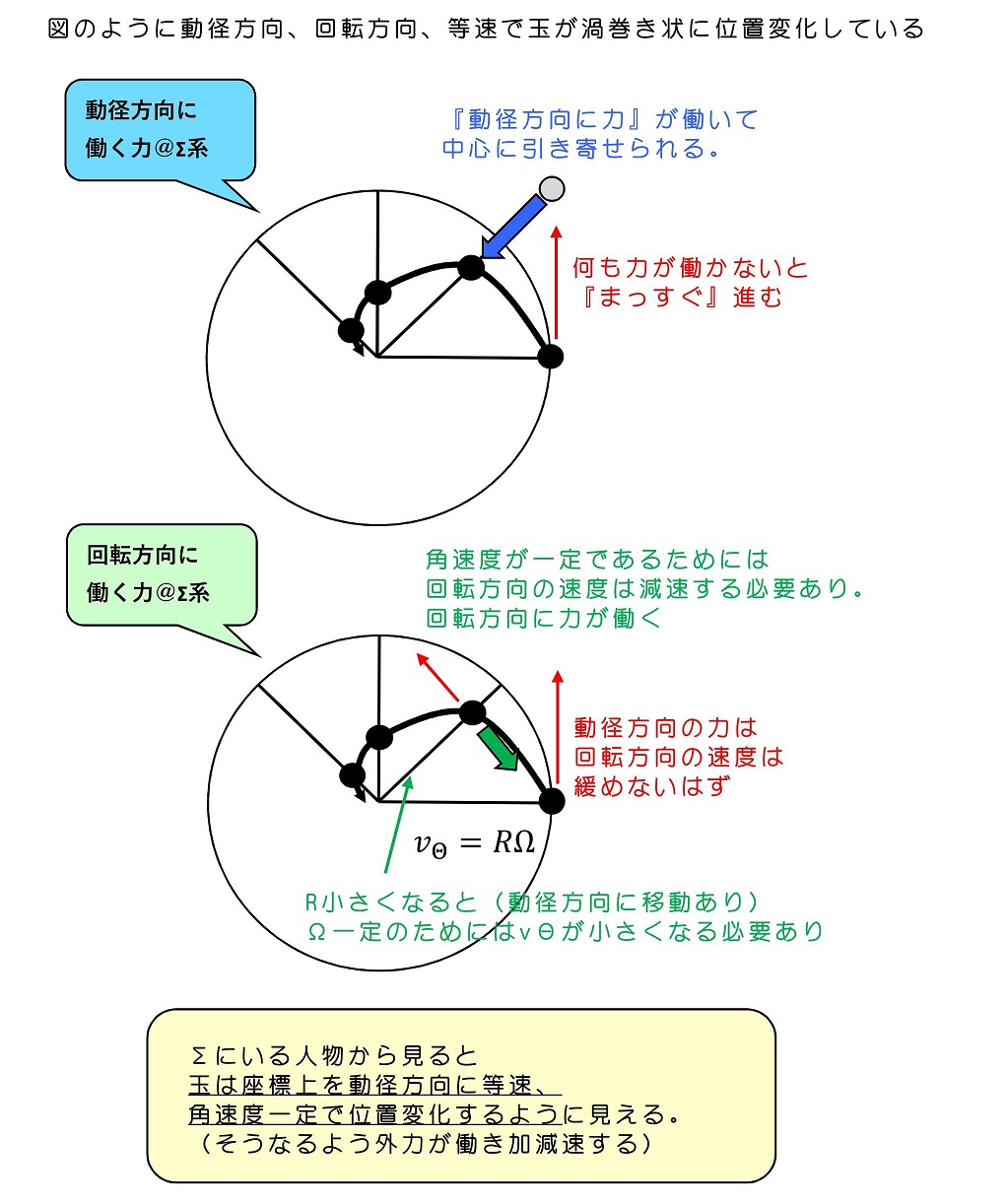
玉と一緒に動く座標系(原点に玉が固定されている)を考える
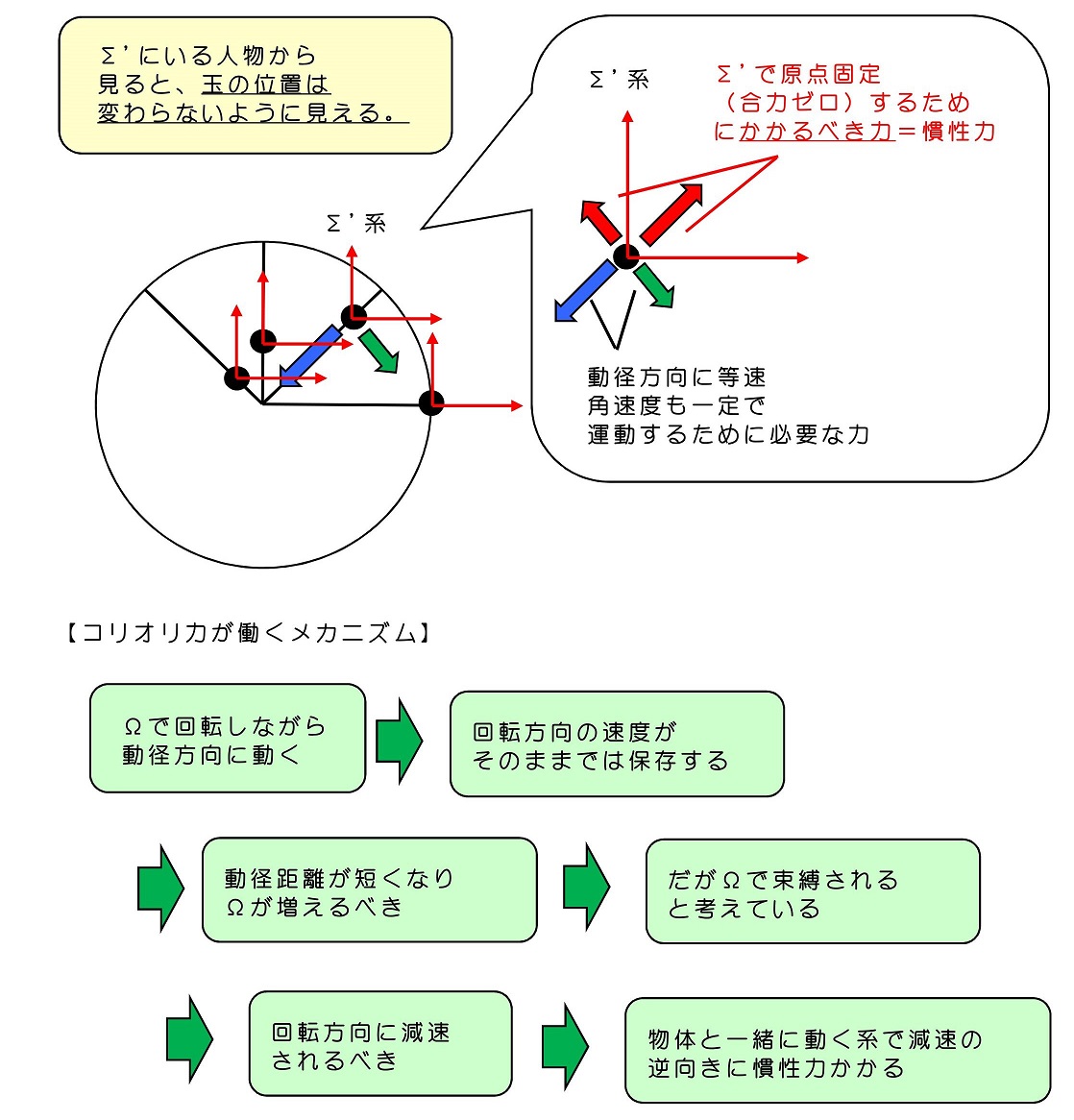
11.6 3次元回転座標系での慣性力
さて、ここまでは2次元回転座標系での慣性力を記述してきた。しかし我々のいる世界は3次元で運動を記述するため、3次元に拡張しておくと便利である。Σ系と原点を一致させながら回転しているΣ'系と、Σ'に固定されたベクトルA'の時間変化を考えてみよう。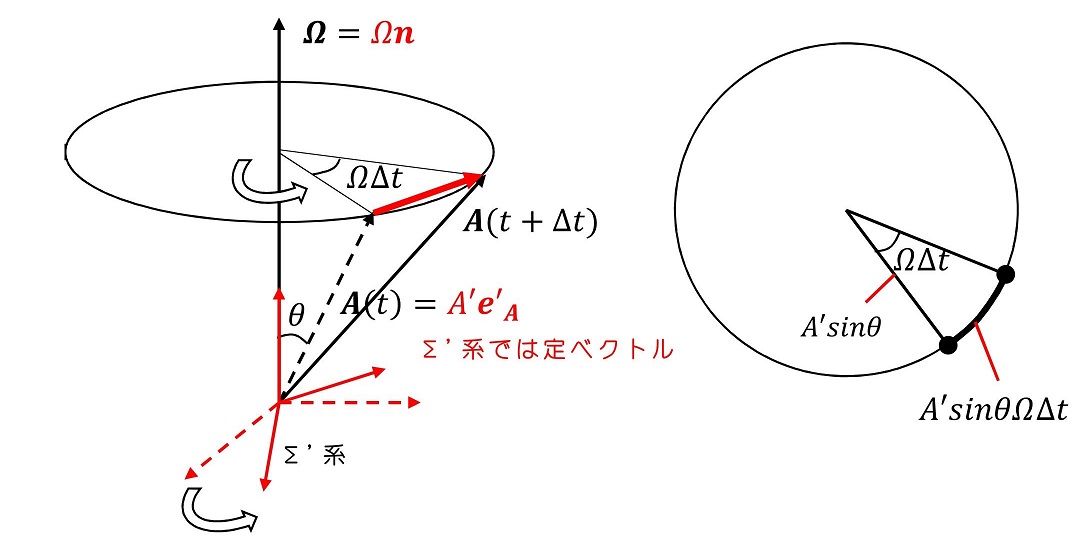
回転に対して右ねじの進む向きに単位ベクトルnをとって、角速度の大きさΩをかけることでベクトルΩを定義しよう。回転とともに動く座標Σ'系から見ると時間変化しないベクトルA'が存在する。回転外部の座標系Σから見ると、ベクトルA'は時間変化している。これをベクトルA(t)と置く。Σ系から見た位置ベクトルA(t)の時間変化はΣ'系のベクトルA'を用いてどのように表せるか?

回転座標系Σ'と外部の座標系Σの関連が見えてきた。Σ系任意のベクトルの時間変化は、回転座標系Σ'から見ると、回転を表すベクトルΩとΣ'系で常に一定の向き、大きさを持つベクトルの外積で表すことができる。さらにΣ'系から見ても時間変化(ベクトルA'が変化する)場合も考えよう。Σ'系での時間変化も足されるわけだ。
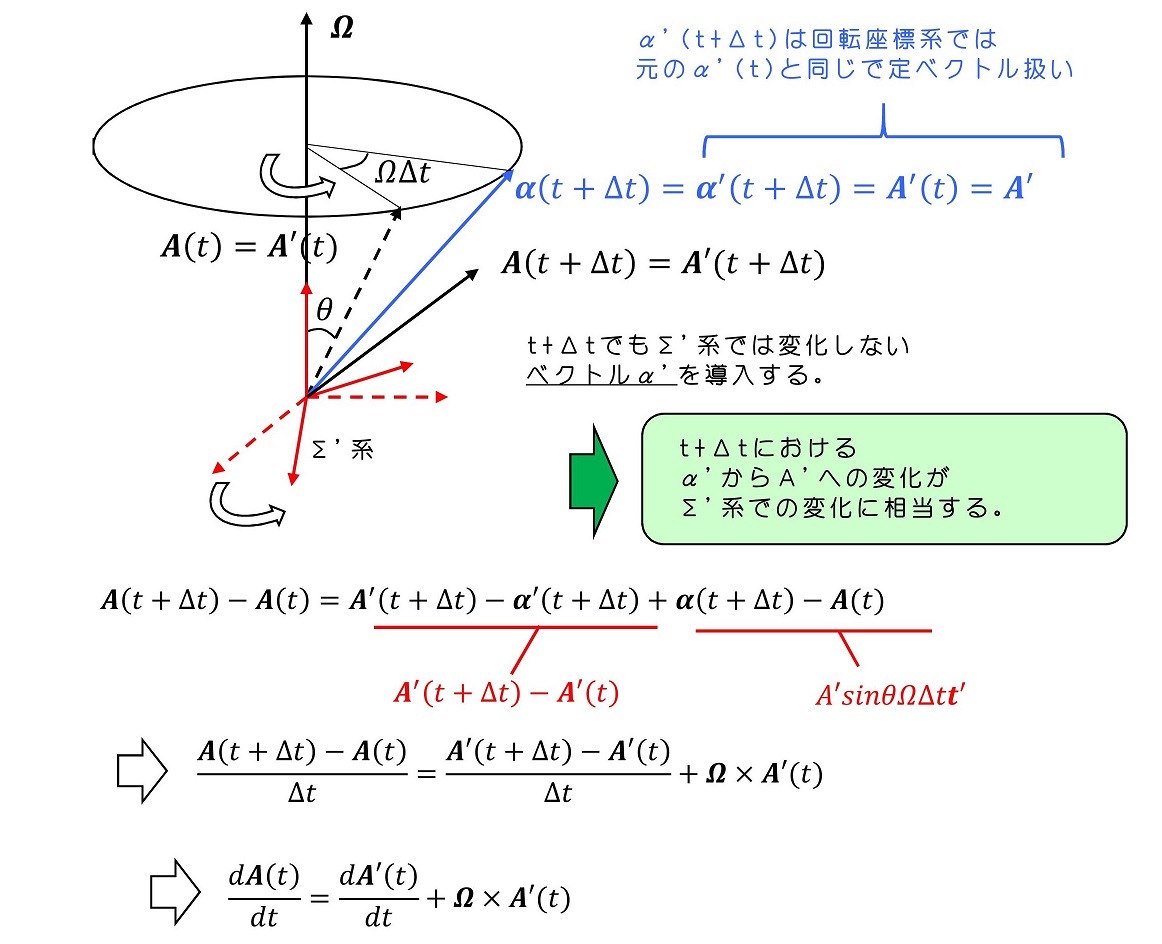
外部の座標系における任意のベクトルの時間変化を、回転座標系Σ'のベクトルとして表す準備が整った。運動方程式は位置座標の時間微分によって表される。今、Σ系における位置ベクトルと速度ベクトルを、Σ'系で表してみよう。
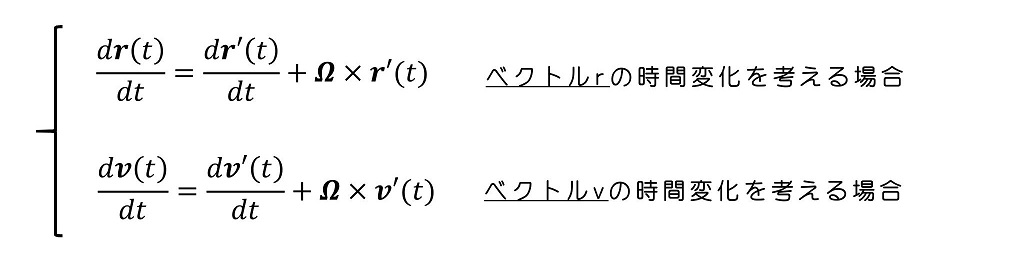
この式のきわめて重要な事実の一つであるが、2つの式は時間の1階微分までしか耐えることができないということである。我々が最終的には位置座標を求めたい以上、位置座標の『2階微分』を考えて、運動方程式を解くべきだが、上記は時間の1階微分までしか扱っていない。

もしも、Σ'系が直線的に等速に変化する座標系であれば、何の苦労もないが、回転という加速度運動をする座標系であることが、やはり問題である。ではどうするか?

さて、ここまで来て、Σ系での位置ベクトルr(t)の2階微分を考えよう。
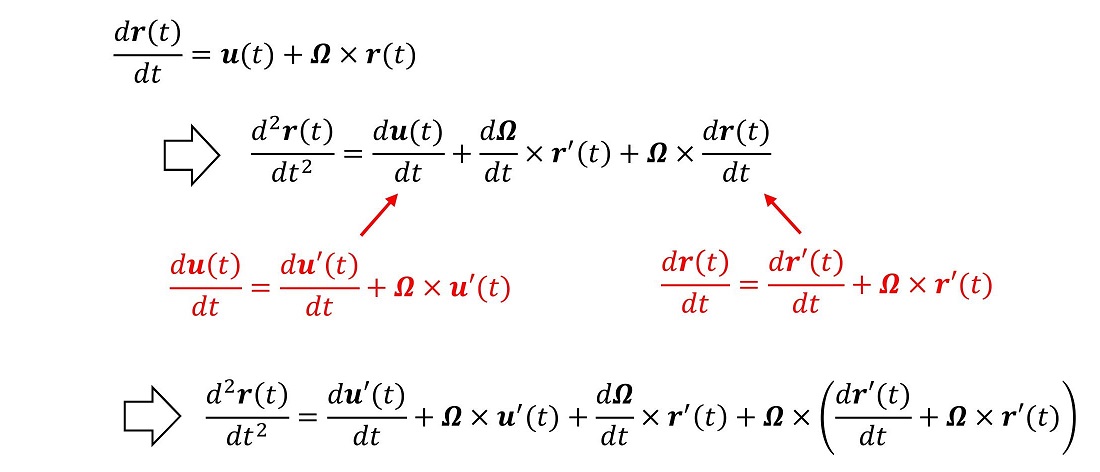

かなり複雑な形だが、これがΣ系の加速度を、回転座標系の位置ベクトルを用いて表すことができたね。Σ系で運動方程式が成立する場合、Σ'系ではどのように見えるか?
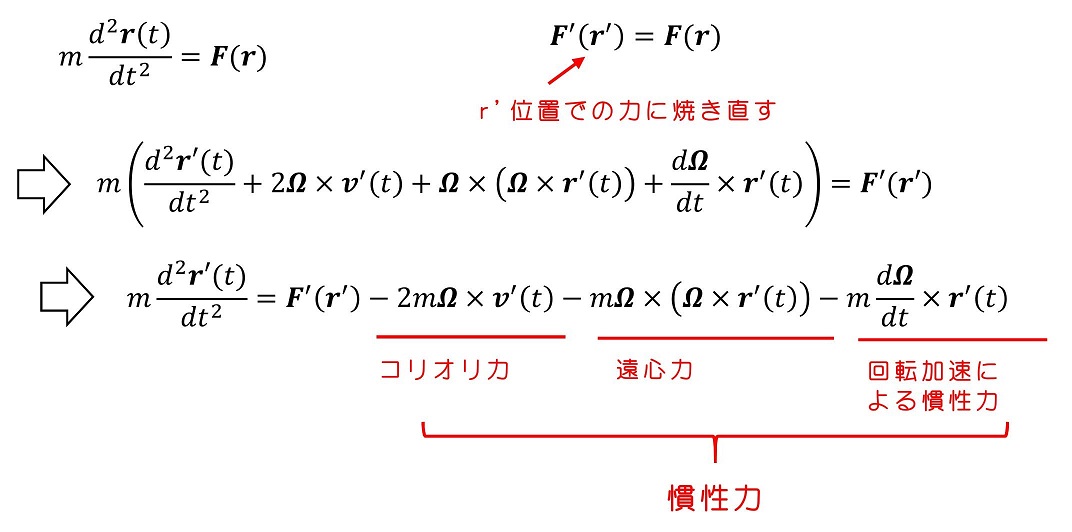
Σ'系から見ると、自身が回転運動していることによる慣性力が見えない力として働くことがわかるね。
11.7 地球に表面における慣性力
最も身近な『回転』は地球の自転である。地球は北極と南極をつないだ地軸の周りに回転している。直感的に、人間は頭上にz軸、前方斜め90°をなしてy軸とx軸を見出しがちだが、地球上に人間が存在している以上、それは回転座標である。回転座標である以上、慣性力が働いている。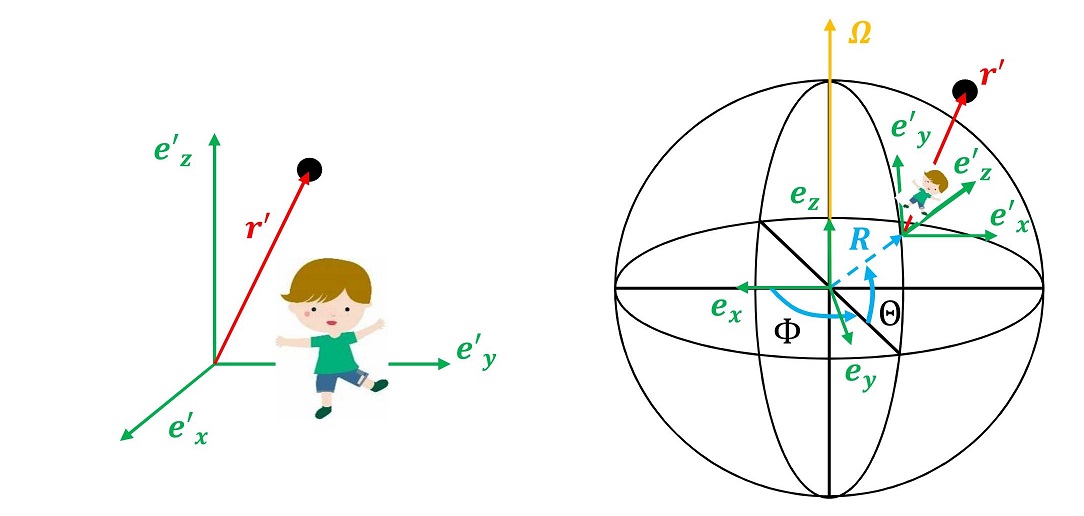
11.7で議論した式を応用することで、地球表面に存在する座標系に働く慣性力を把握することができる。とはいえ、次のような違いがあるため、対応をまとめておこう。

11.7ではもともとはΣ'系として、Σ系と同じ原点で、Σ系とz軸を共有しながら、角速度Ωで回転する座標系を考えていた。これは、図を見やすく、考え方を直感的に容易にするための措置であり、一般的にはΣ'系はΣ系と原点が一致しなくてもよいし、z軸も一致しなくてよい。一般化するにあたって上記の対応を行って、式を記述しなおせば、問題ない。
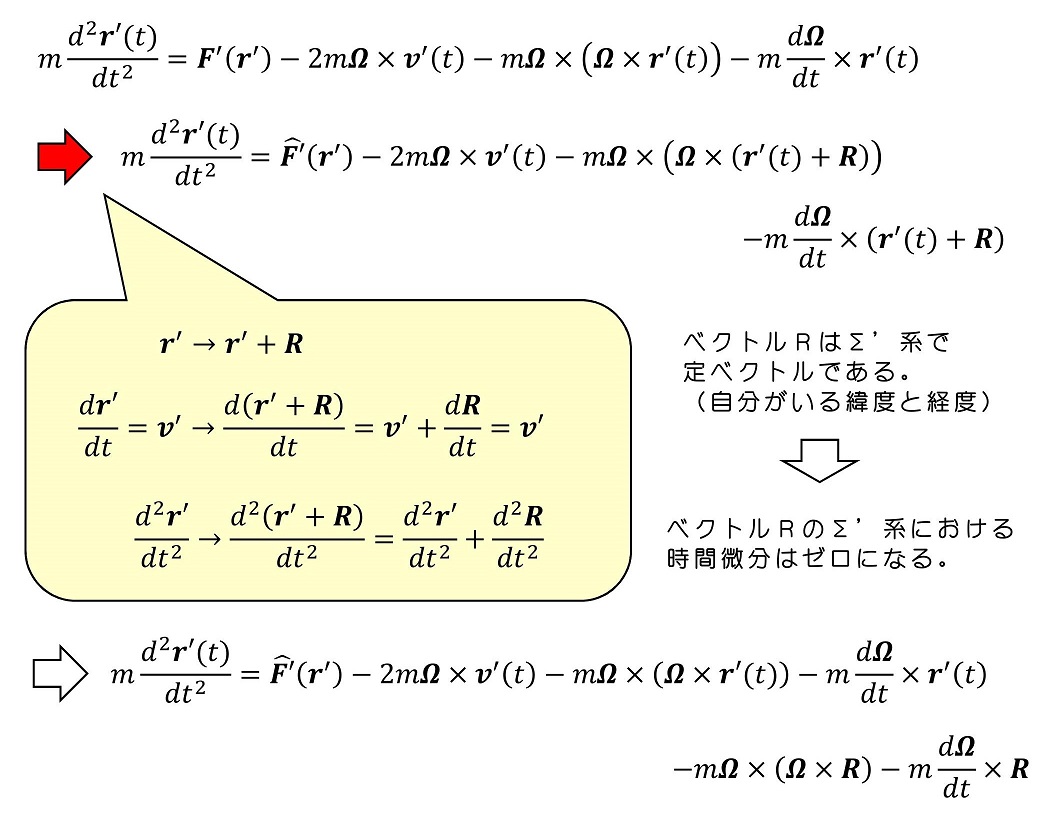
地球の場合、回転の角速度は一定であり、24時間で1回転する。また、我々が周囲で見かける物体の位置はせいぜい100m程度の範囲の運動であり地球半径を表すR=6400kmに比べはるかに小さい。これを用いて、もう少し式を簡略化しよう。
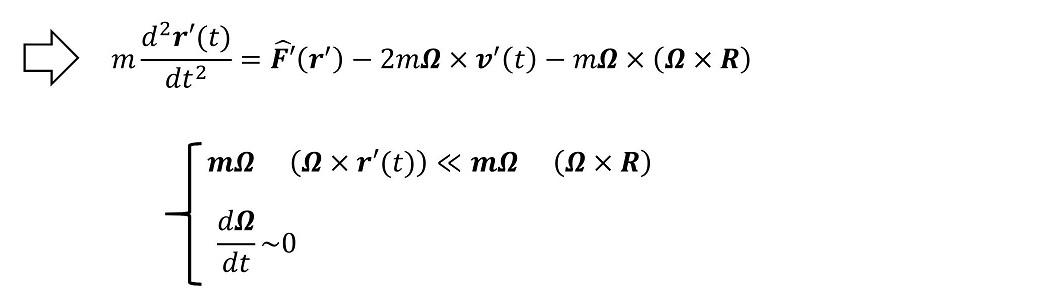
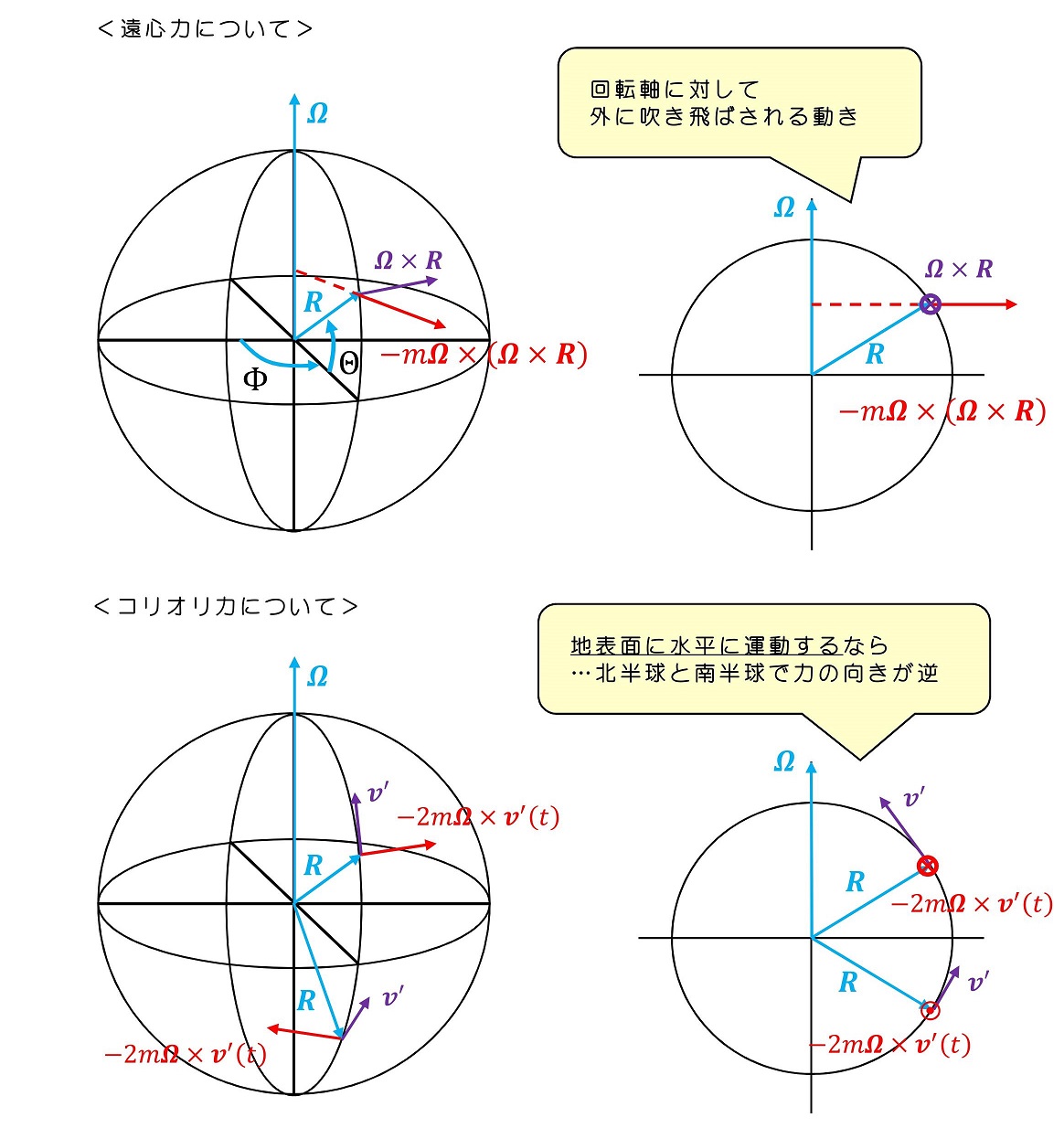
地球表面上で具体的にどのような向きに力が働くのかを整理しよう。
11.8 フーコーの振り子
地球上で働く慣性力(遠心力やコリオリ力)は実際にはかなり小さい。そのため、我々は慣性力の存在にあまり気づくことなく暮らすことができる。それぞれ定量的に大きさを調べてみよう。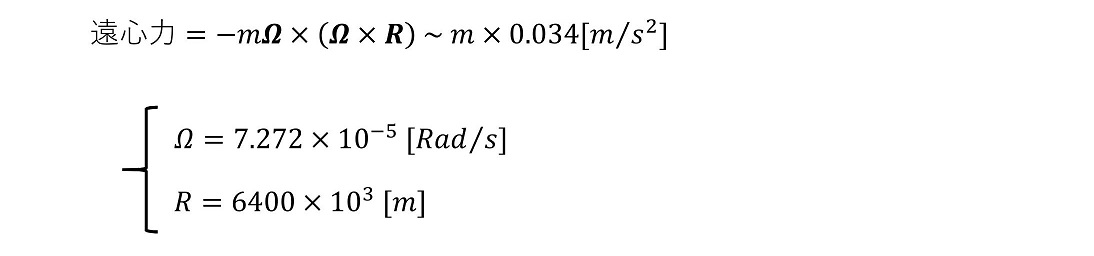
遠心力は回転軸に対して、外に引っ張られる側に、つまりわずかに地球の重力を軽くする側に働いている。重力加速度gは9.8m/s2である一方、遠心力による加速度は0.034m/s2であり、重力加速度の0.3%程度にしか及ばない。ほとんど無視できるだろう。
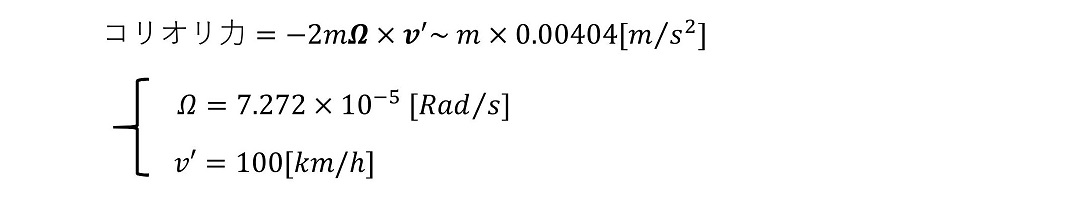
時速100kmの投球に働く進行方向横向きの力を計算したことに相当する。等加速度でこれだけの力が進行方向横向きに働く場合、その影響はどれほどになるか?

我々の身の周りの運動に対して、コリオリ力も与える影響は極めて小さいことがわかる。遠心力を実感するのは難しいが、コリオリ力を実感することは振り子を用いれば可能である。北半球では進行方向に対して右方向の力が常に働くわけであるから、振り子運動では往復それぞれで働く力の向きが逆転し、緩やかに回転運動をするはずである。揺らし始めたタイミングから、数時間経過して再度観察すると、おそらく振り子のふれる向きが変わるはずである。
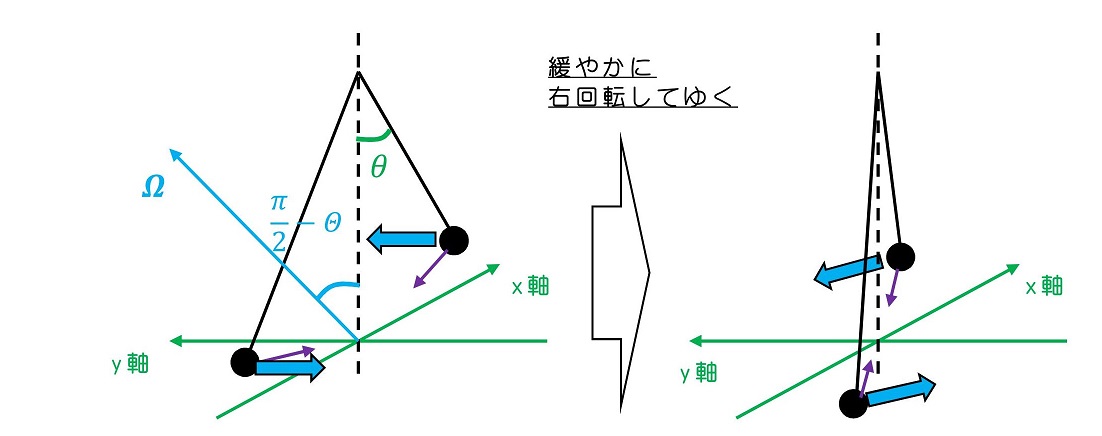
ひもの長さと比べ、振幅が小さい場合、単振り子と同様に鉛直方向の動きをほぼ無視することができる。ここで、地球の自転による遠心力は重力に非常に小さいため無視する。コリオリ力は今回着目したい力であるため考慮に入れる。地球の自転をあらわす角速度ベクトルΩは鉛直方向に対して傾いているため注意する。
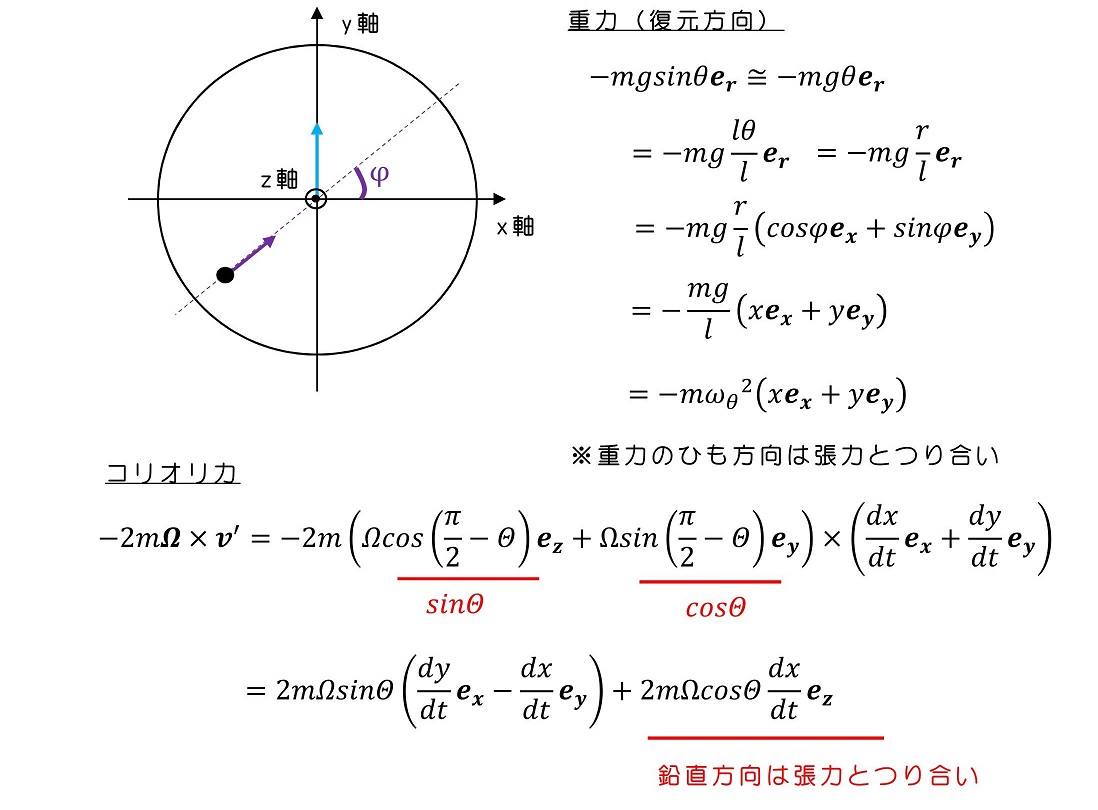

2階1次の連立微分方程式である。うまく関数xかyを消去することで解が得られる。
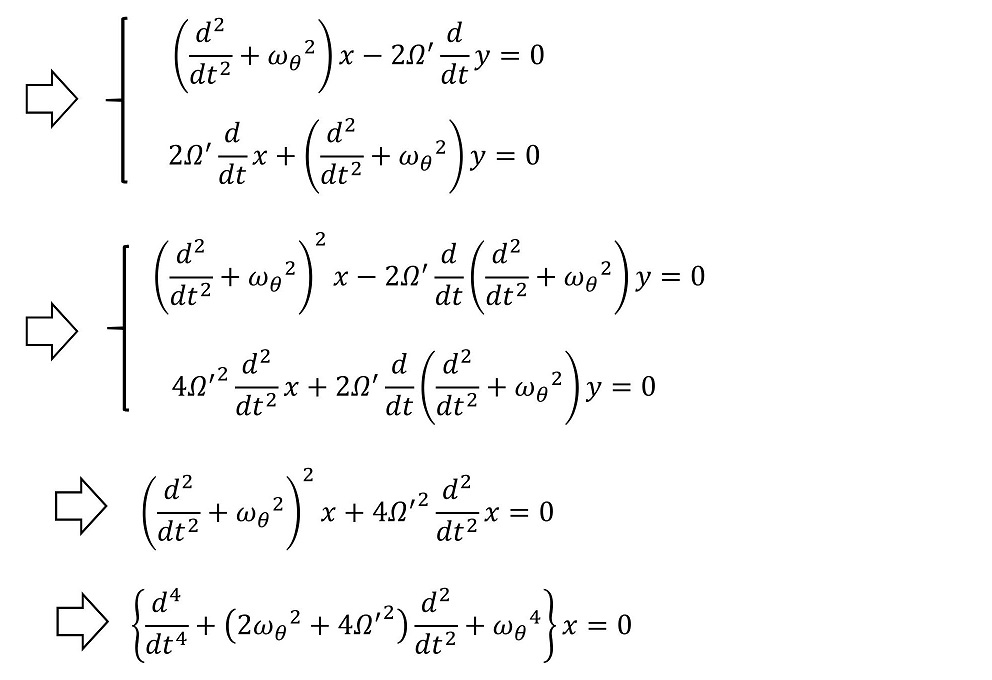

いったんここで式変形を止めておく。このxを用いてyも計算する。

2次元平面での2階微分方程式のため、不定定数は4つ存在するはずである。これを決定するのはx方向とy方向の位置、速度の初期値である。

この4つの未定定数を代入することで、運動の軌跡を求めることができた。しかし、かなりまだ煩雑である。実はΩとωθについて定量的に評価すると、近似的に式を簡略化することができる。

原点からの距離および、x軸からなす角を求めてみよう。
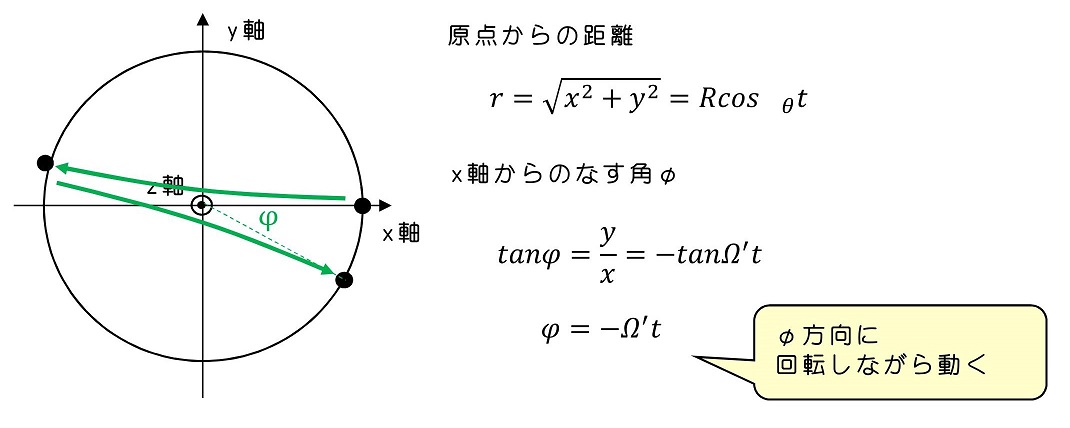
Ω'が正の時、徐々に時計回りに変化(進行方向右がわに力をうける)ように軌跡を描くことがわかる。Ω'は地軸の回転速度と緯度の正弦値で表される。Ω'が正とは、北半球ということである。

試しに、北緯30°の場合を計算してみよう。角速度が1/24時間の半分になるため、玉が反時計周りに変位して元の位置(x軸上)まで戻ってくるためには48時間かかることがわかった。