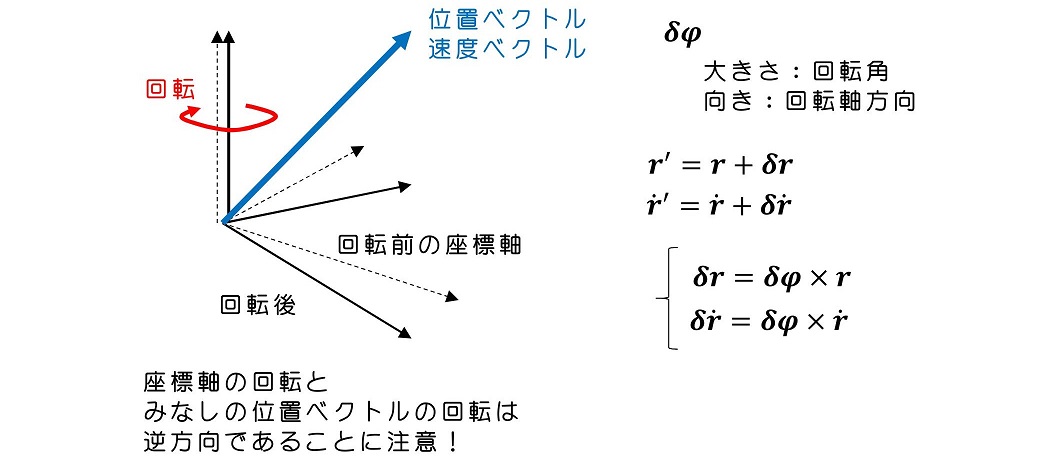
12.1 力学を再構築しなおそう
『運動の軌跡はニュートンの運動方程式に従って記述される』と考えるのが、歴史的順序にも従っており非常にわかりやすいが、ベクトル方程式であるため解を求めるのに苦労したり、座標系のとり方(極座標系など)で式がかなり複雑になったり、多粒子系の記述に弱かったりと、苦労することも多い。そこで、まったく新しい運動の記述方法が誕生した。この章で紹介する、ラグランジュの運動方程式を用いれば、運動の記述が一気に容易になるだけでなく、自然界に潜む物理法則の美しさも目の当たりにできるだろう。
まずは、いったんニュートンの方程式の存在を忘れ、次のように運動の軌跡が決定されるという、抽象的な法則を受け入れよう。その後、取り扱った抽象的な方法が、ニュートンの運動方程式を帰結として導けることを紹介しよう。

作用の具体的な意味:座標空間での軌跡とは?
作用の意味を理解するのは、案外難解である。まずは作用の積分の軌跡と実際の軌道を対応づけて、意味を理解したい。
<初期停止しており、一様重力下で落下する運動>
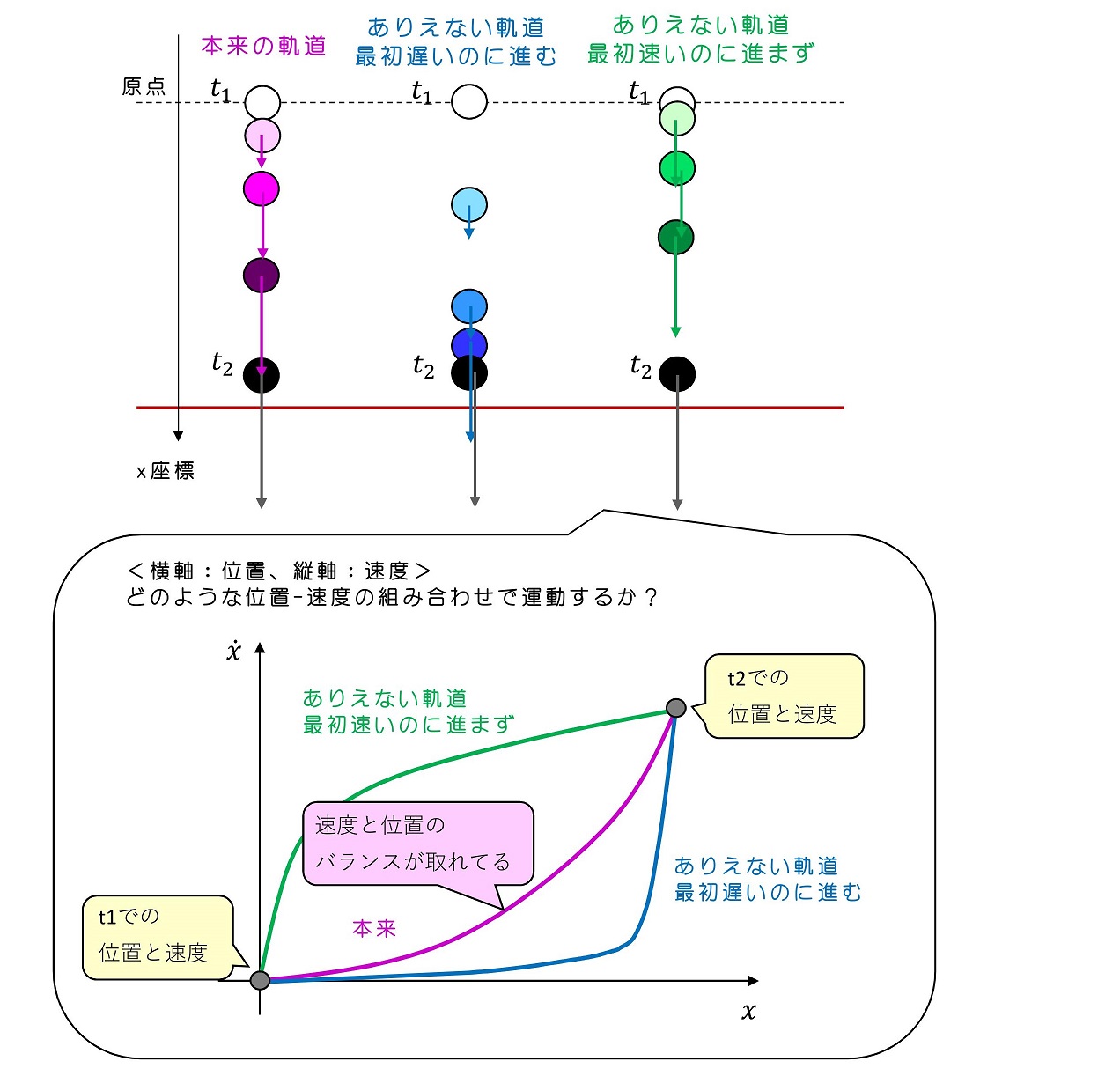
初期状態と終状態を同じにしても、その間の位置と速度の値のとり方は 無限に存在する。場合によっては、速度が遅いはずなのに、位置がどんどん進んで行ったり、逆に速度が速いはずなのに。位置が進まなかったりするパターンである。バランスのとれた位置と速度の組み合わせは、どのように決定されるだろうか?
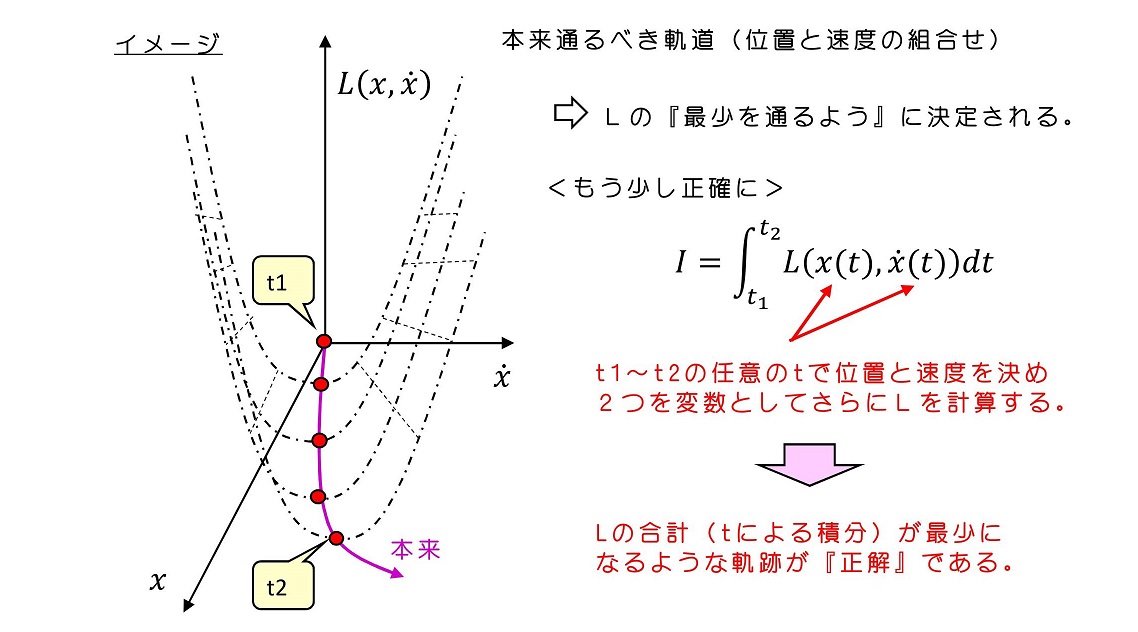
作用を最少にするような軌跡が、実際の運動軌道を表すような関数Lはどのような形をしているのだろうか?ここでは、若干天下り的だが、次のように関数Lを与えてみよう。
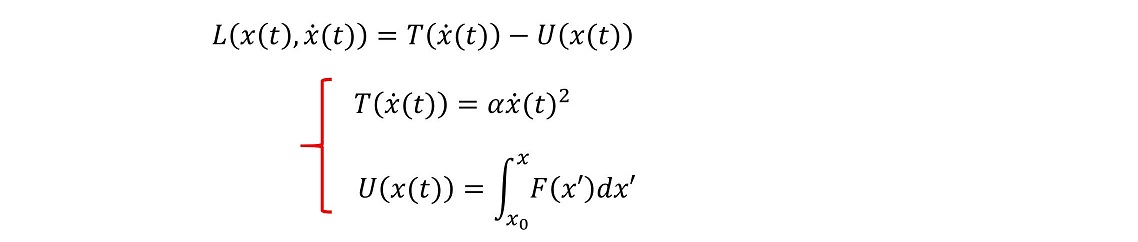
作用を最少にするような、xをどのように求めればよいのか?それには汎関数の変分という数学的手法を用いなければならない。
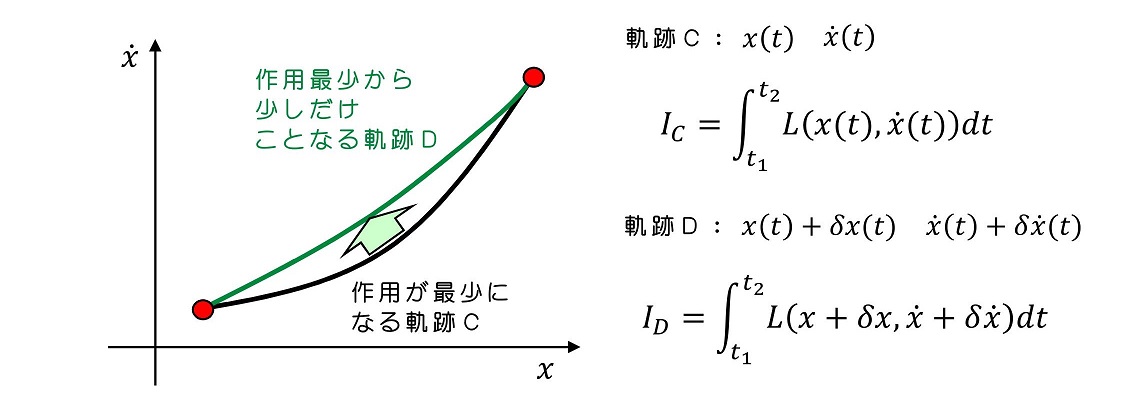
軌跡がわずかに異なったことによる作用の差を求める。

軌跡の変化のさせ方δx、δxドットは無数に存在するが、いかなるδに対しても作用の変分がゼロであれば、現在選択しているx、xドットは作用を最少にするような軌跡だと判断できる。

運動方程式との比較により、TやUという関数が、具体的な物理量として与えられる。

ここまで検討してみて、次のことがわかった。

12.2 3次元でのラグランジュ方程式
一般に、粒子は3次元空間で運動する。そのため、最少作用の法則も3次元空間でのものになる。とはいえ、若干抽象さが増すのみであり、それほど困難でない。1次元運動であれば、作用を計算するとき、位置と速度の2次元空間であった。3次元運動であれば、作用は6次元空間での積分になると予想される。
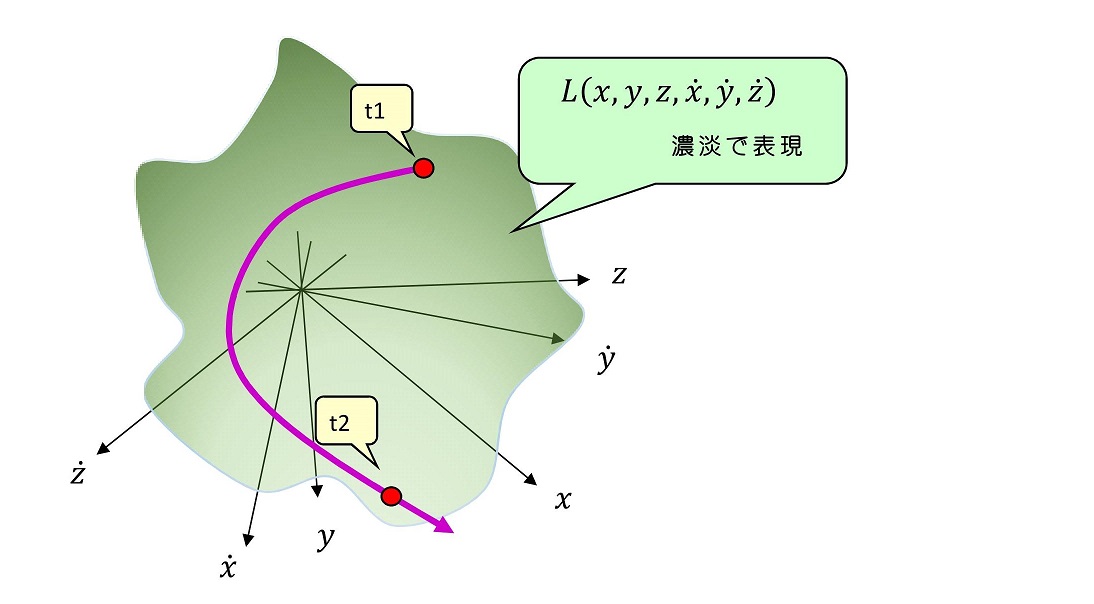
紙面の上で、6次元空間の絵をかくことが不可能なので、あくまでイメージである。数式上では、作用の大きさは次の式で表される。


また、この場合のLも3次元の運動エネルギーとポテンシャルエネルギーを用いて記述すれば、ニュートンの運動方程式が、ラグランジュの運動方程式と等価になることが示せる。

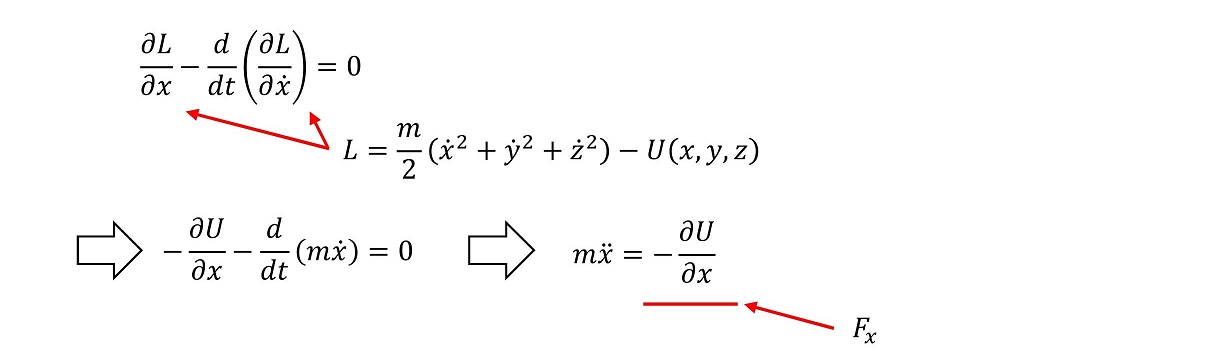
同様に、y方向とz方向も計算可能であり・・・

12.3 慣性の法則とガリレイの相対性原理について
ラグランジアンおよび、その運動方程式を見れば、慣性の法則およびそれに付随して相対性原理についても自明であることがわかる。ポテンシャルが働くと、力がかかるのと同じであるため、慣性の法則とは別の問題になる。ここでは力の働いていない粒子(自由粒子)のラグランジアンを考えていこう。
自由粒子のラグランジアンと空間の一様性
慣性の法則のもう一つの大前提として、空間が一様等方であり、時間も一様であることが前提とされている。自由粒子のラグランジアンは空間の等方性と密接な関係がある。
もし、自由粒子のラグランジアンがx,y,zを明らかに含んでいた場合、どのようになるだろうか?

自由粒子のラグランジアンと空間の等方性
また、ラグランジアンは必ず速度の大きさの関数である。もし、ラグランジアンが速度の大きさ以外に依存すると、運動方程式がx方向、y方向、z方向で非対称になってしまう。

x方向の運動方程式にはxドットが、y方向、z方向も同様にyドット、zドットが明らかに含まれている。それ以外は、対称なvの関数である。いま、特定の方向にx、y、zを選択したが、この向きを別の向きに選択しても、方程式の形が変わるわけではない。


自由粒子のラグランジアンとガリレイ変換
現在対象としている座標系をΣとし、Σ内で等速直線で原点が移動している座標系をΣ’と呼ぶ。Σで見ても、Σ’で見ても、自由粒子は速度の大きさと向きは異なっているが、いずれも等速直線で動くことに差はないはずである。Σ’の座標系に変換する操作をガリレイ変換と呼ぶ。ガリレイ変換に伴い、ラグランジアンはどのように変化するか?

さて、ここで自由粒子のラグランジアンが、v2の定数倍であると仮定しよう。この時、Σ'系におけるラグランジアンと、ラグランジュの運動方程式はどのように変化するだろうか?
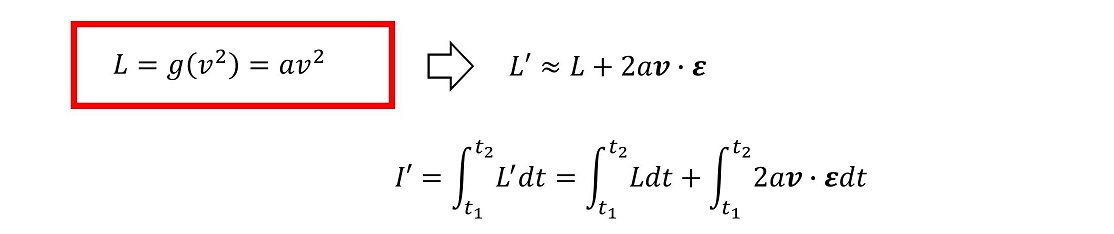
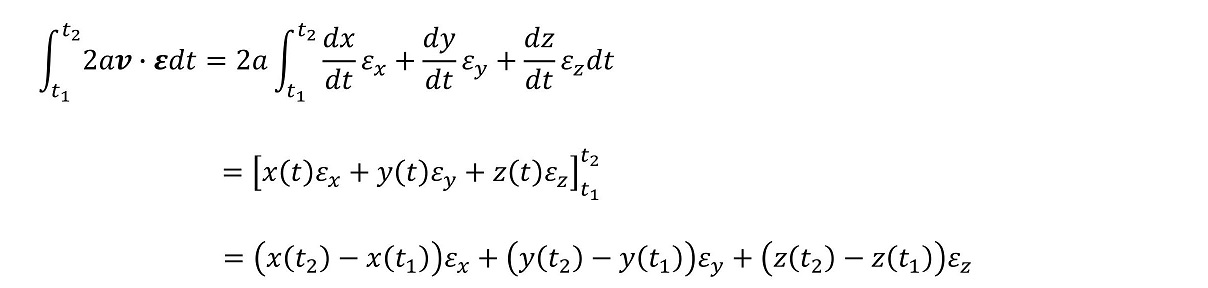
ここでt1の時とt2の時の位置は固定した場合に、どのような運動経路をとるかが論点だから、実質この積分は定数になる。

非常に興味深い事実をはらんでいる。自由粒子のラグランジアンが速度の2乗に比例すると仮定した場合、Σ系に対して等速直線に、ゆっくりと運動しているΣ'系で作用を計算しても、その最少となる経路はΣ系で作用を計算した場合の最少となる経路と一致することが証明できた。
等速直線で運動する微小な速度ベクトルを無数に重ね合わせることで、任意の等速直線運動を再現できる。ある座標系で作用が最少になる経路であれば、そこから微小な速度ベクトルで等速直線運動する座標系でも作用が最少になることがわかり、さらにそこから微小な速度ベクトルで等速直線運動する座標系でも作用は最少となり…を繰り返し、ある座標系で作用が最少になる経路は、任意の経路での等速直線運動する座標系での作用を最少にする経路であると推定できる。これは、運動方程式が等速直線運動をするいかなる系でも等価であるというガリレイの相対性原理に対応している。

自由粒子のラグランジュ方程式と慣性の法則
自由粒子のラグランジアンは、空間の一様等方性とガリレイ変換に対して共変であるという事実から、vの2乗に比例するという事実が導かれた。このラグランジアンをラグランジュ方程式に代入することで、『力が働いていない質点』は『速度一定で運動を続ける』という慣性の法則が導ける。

12.4 多粒子系への拡張
粒子が1つの場合は、3次元の位置及び速度でラグランジアンが記述されるため、6個のパラメータすなわち6次元空間内でのラグランジアンの作用を求め、その最少となる経路を物理的に実現される経路と考えればよかった。同様の考え方を多粒子系でも拡張して運動を記述することができる。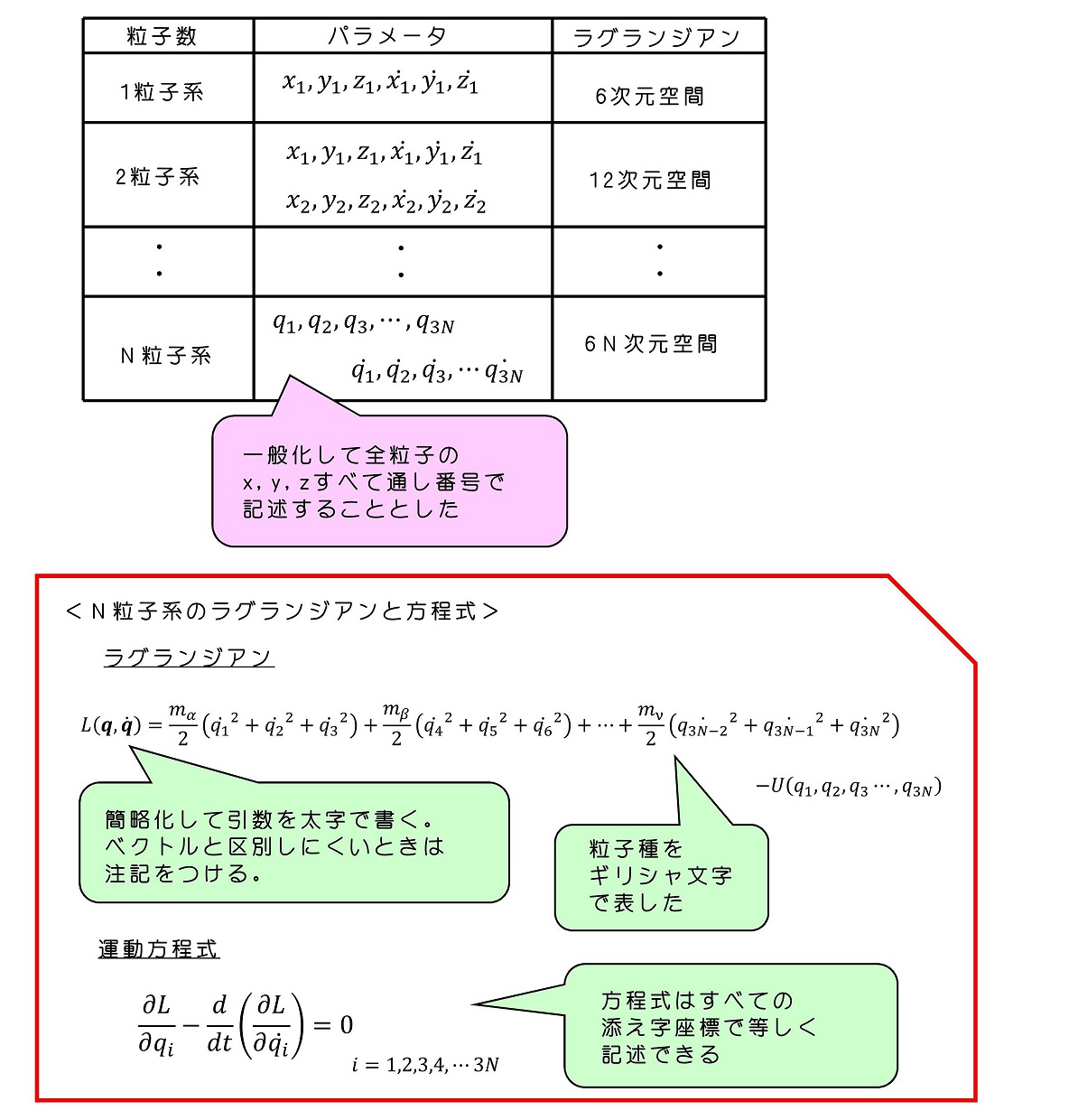
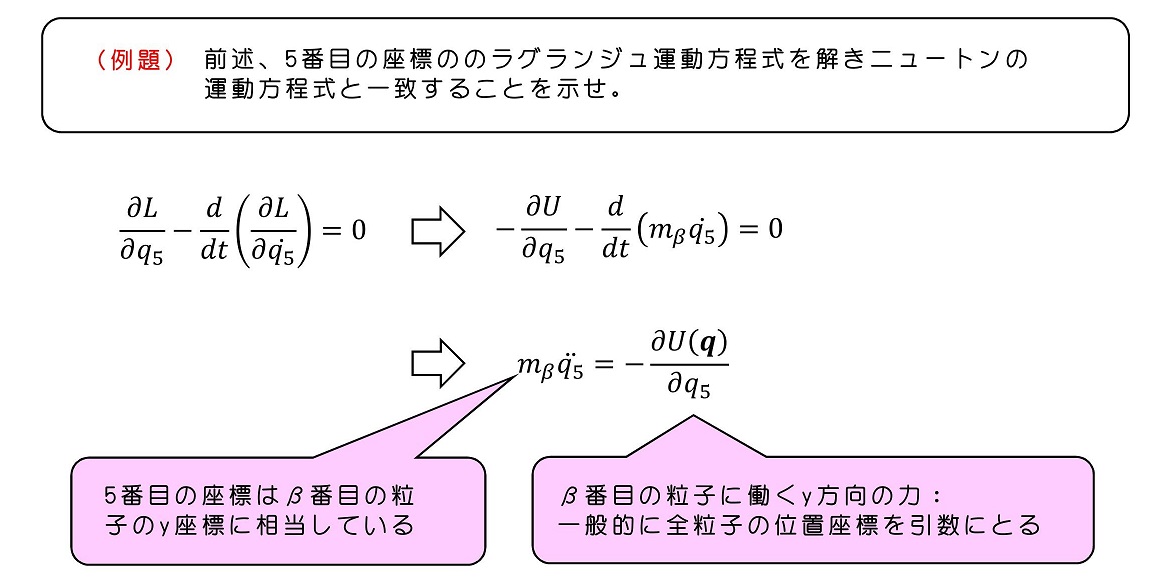
N粒子が相互に孤立している場合のラグランジアン
ラグランジアンを構成するポテンシャル項に注目しよう。一般に、α番目の粒子はβ番目やγ番目の粒子からも影響を受けるため、α番目の粒子の運動方程式(1番目から3番目の座標)の力の項は、β番目の粒子の座標やγ番目の粒子の座標にも依存する。しかし、それぞれの粒子が孤立している場合(粒子間の相互作用がない場合に相当)ポテンシャル項は次のように分離できる。これは、粒子の質量を全宇宙、統一単位で表せることに関連している。
<全粒子が孤立している場合>

12.5 ラグランジアンの不定性について
運動を記述するためのラグランジアンは運動エネルギーとポテンシャルエネルギーで表すことが「できる」わけだが、単純にそれらで記述する「必要もない」ことが示せる。簡易にラグランジアンを求める手法として、L=T-Uという一般化がなされているが、実際には最少作用となる経路を実現できる所定の関数であれば、なんでもよい。以下で具体例を示そう。定数項を足す
L=T-Uで表せるラグランジアンに、任意の定数を足し合わせたものを新たなラグランジアンであるとしても、作用が最少となる運動経路は一致する。
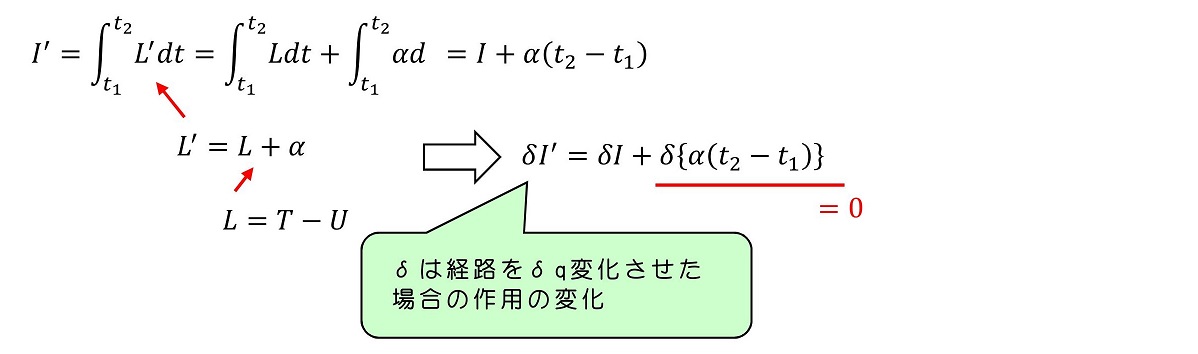
δIがゼロ場合、δI'も必ずゼロになる。運動の経路は変わらないため、L’も正しく運動を記述するラグランジアンである。
定数倍する
L=T-Uで表せるラグランジアンに、任意の定数を掛け算して新たなラグランジアンをつくっても、作用が最少となる運動経路は一致する。
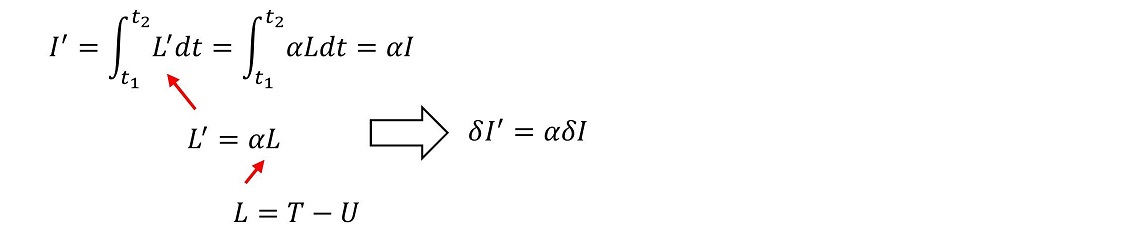
δIがゼロ場合、δI'も必ずゼロになる。運動の経路は変わらないため、L’も正しく運動を記述するラグランジアンである。
時間にのみ依存した可積分関数を足す
L=T-Uで表せるラグランジアンに、時間にのみ依存した(経路には依存しない)積分可能な関数を足す。

δIがゼロ場合、δI'も必ずゼロになる。運動の経路は変わらないため、L’も正しく運動を記述するラグランジアンである。


12.6 ラグランジアンと運動の相似について
質量やポテンシャルなど、系を構成する要素が全く同一であるにも関わらず、軌道が定数倍になっていたり(もちろん運動の時間もかかる)質量などが異なっているはずなのに、軌道が定数倍になっているといったケースを考えることができる。これを相似な運動と呼ぶ。相似な運動になるための必要条件に付いて議論してみよう。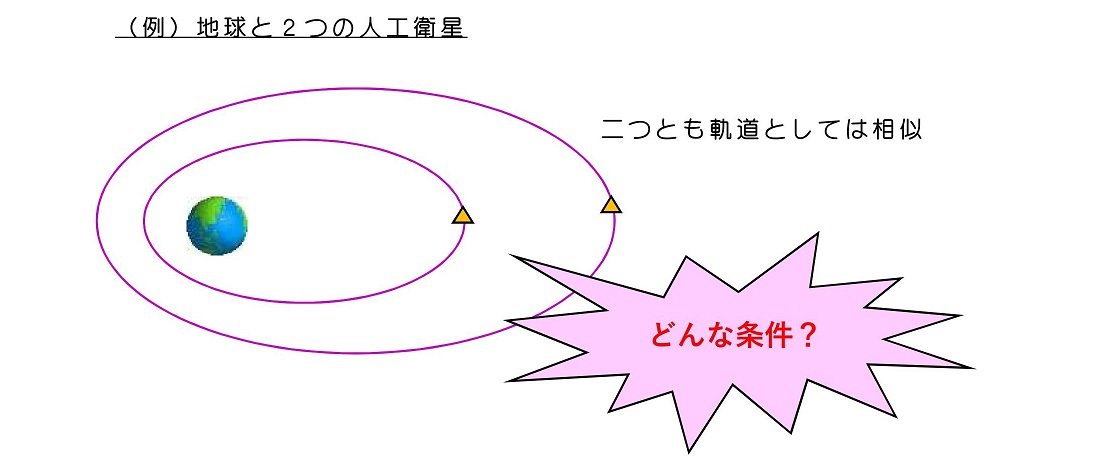
質量やポテンシャルが等しい系
ある運動をΣとする。質量とポテンシャルの形が一緒だがΣの定数倍になるような軌道の運動をΣ’とする。同じ時間で長い距離を運動することもできないから、Σ’では時間も定数倍(単位時間が増えた)と考えてみる。

<ポテンシャルが1/r形状>
万有引力のポテンシャル形状である。
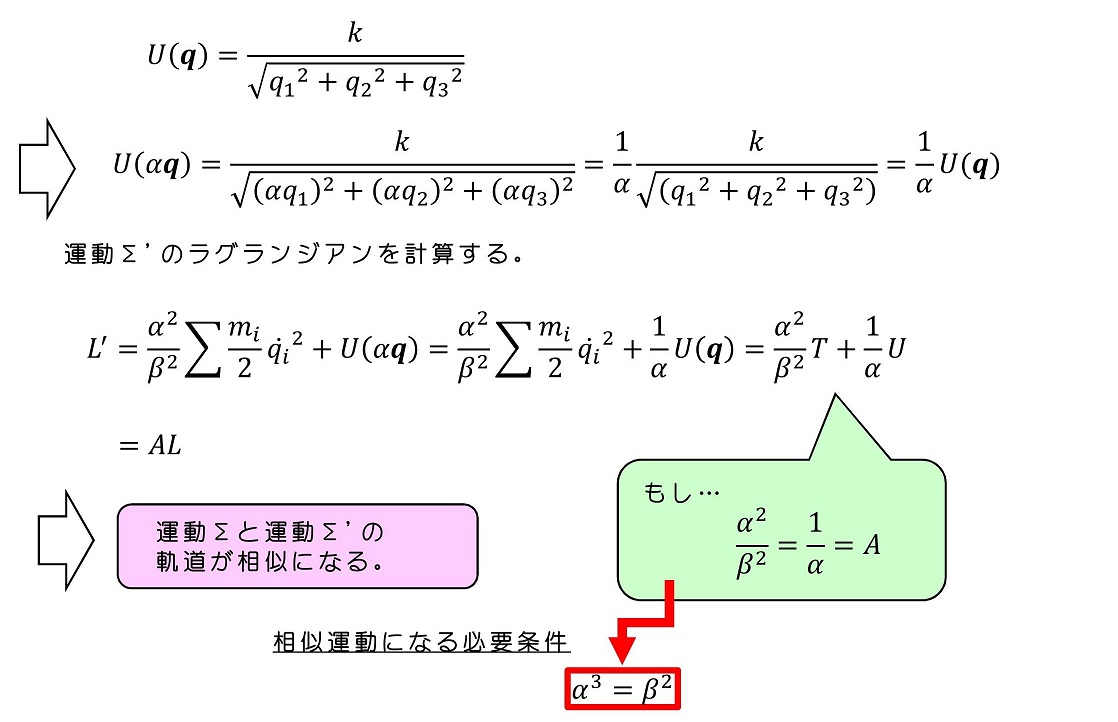
以上の議論は重要な事実を内包している。2つの質量が等しい衛星が相似運動をしている場合、軌道の相似比の3乗が、公転周期の比の2乗に一致するよう運動する。これは、ケプラーの第3法則にも矛盾しない。

<ポテンシャルがx2に比例する形状> ばねによるポテンシャルの形状である。
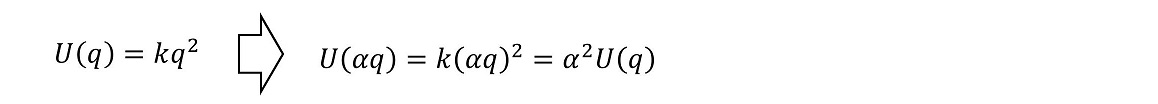
運動Σ'のラグランジアンを計算する。
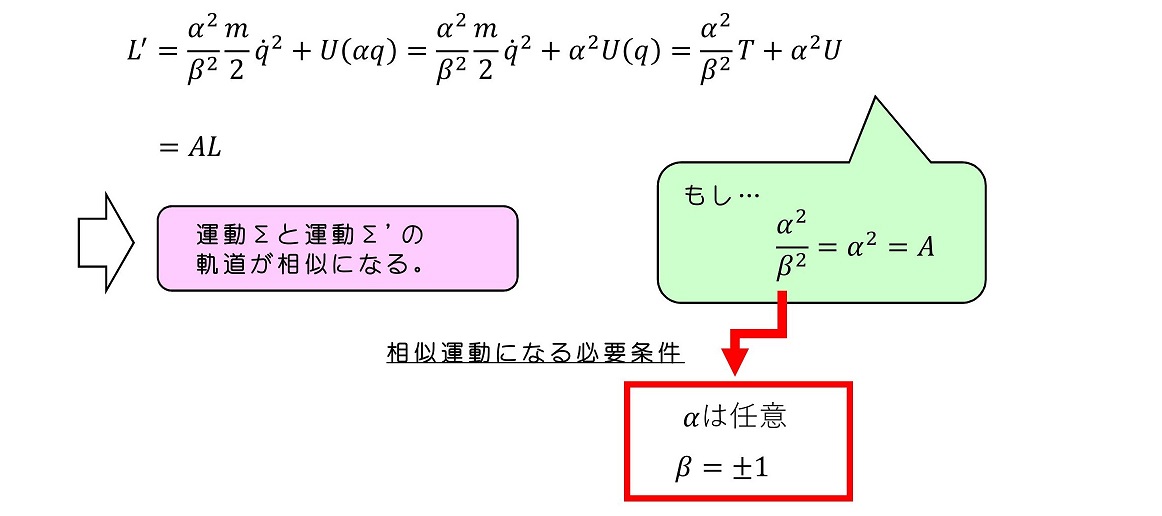
βは単位時間のとり方を表す係数である。時間が正の方向(過去から未来)に流れることを真と仮定すると、β=-1は許容されない。β=+1にも関わらず、αが任意で相似運動になるとは、つまりばね運動の振幅がいくらであっても、周期は変わらないことを示している。
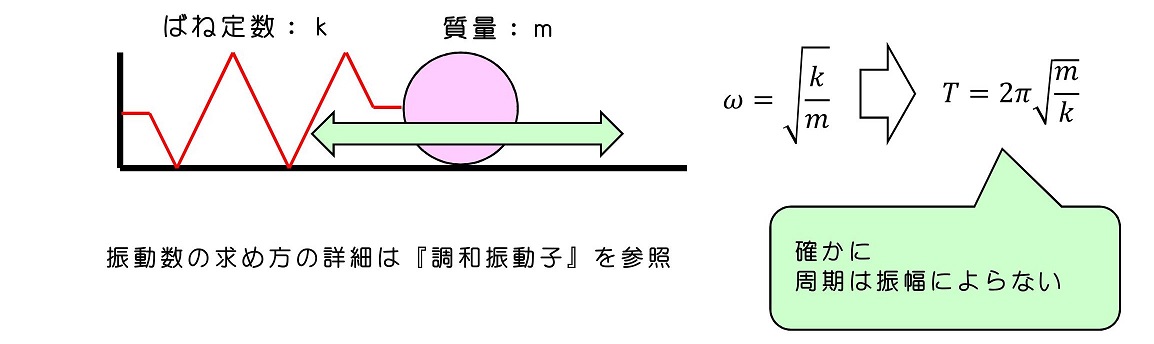
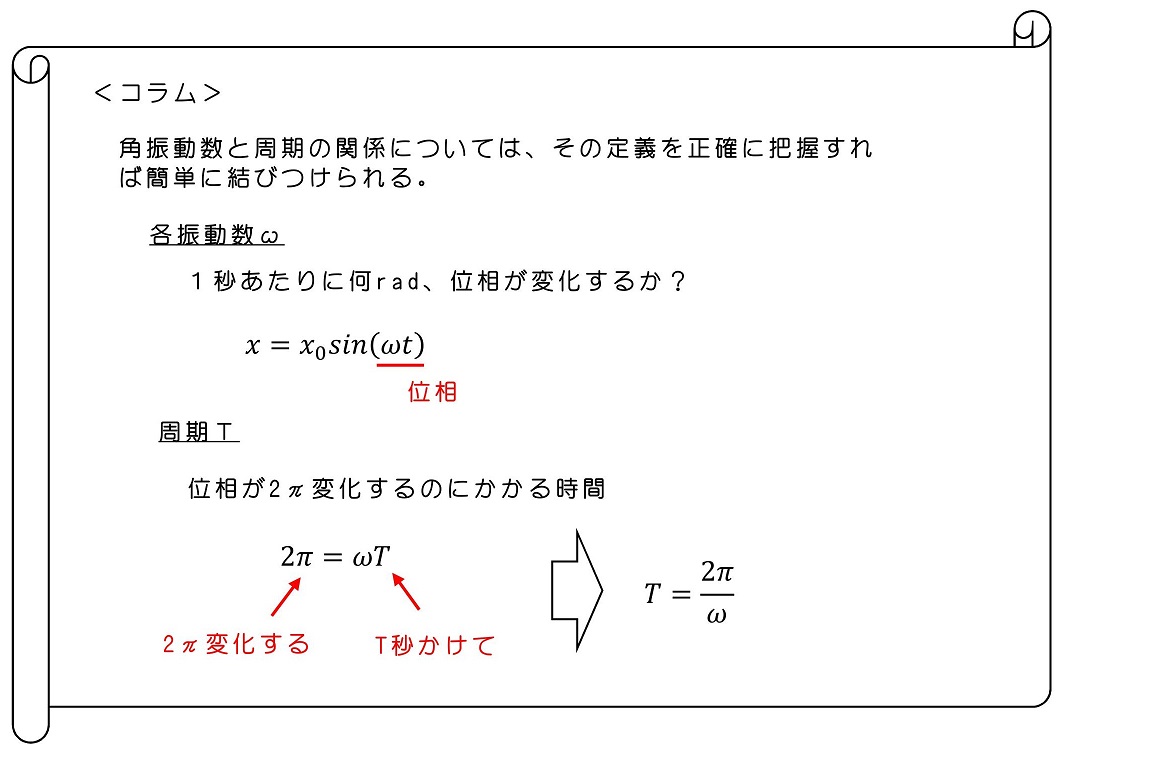
12.7 ラグランジアンと空間や時間の一様性、等方性について
N粒子系のラグランジュ運動方程式は3N個の座標と3N個の速度をパラメータとしており、これを解こうとすると、3N個の2階微分方程式となる。これを解くと、6N個の未定定数が出現する。未定定数とは、運動において一切変化しない量である。すなわち運動における保存量と関連付けることが、必ずできるはずである。時間の一様性からエネルギー保存則が、空間の一様性から運動量保存則が、空間の等方性から角運動量保存則が導かれる。6N個の未定定数のうち、3つの定数はこれら保存量であるべきと、考えることができる。保存量とラグランジアンの関連性を指摘するのが、この章の目的である。
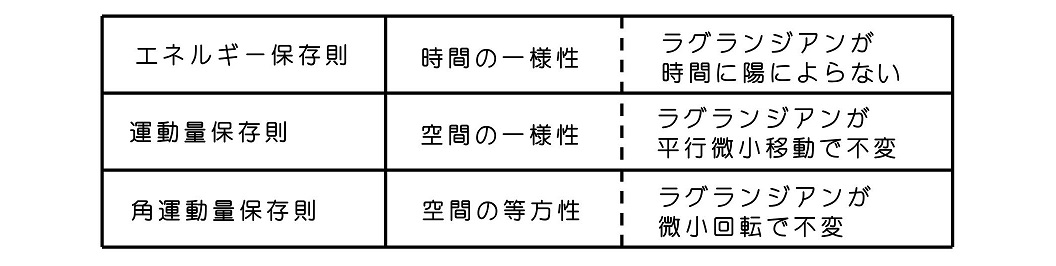
ラグランジアンとエネルギー保存則
エネルギー保存則と時間の一様性は、きわめて密接な関連を持っている。時間の一様性とはどのようなことだろうか?過去から未来のどのタイミングでも、成立する運動方程式が変化しないとき、運動に関して時間が一様に流れていると定義する。(もし、運動方程式が時間によって異なると、どのた時間タイミングでも等価な運動と扱えなくなってしまう)これは、ラグランジアンが時間に陽によらないと言い換えてもよい。

さて、ラグランジュの運動方程式をここで用いよう。

関数hの性質を求めてみよう。簡素化のため、1粒子1次元運動のラグランジアンを用いる。

ラグランジアンと運動量保存則
空間の一様性とは、座標系の原点のとり方を微小量変化させたときに、ラグランジアンが不変に保たれることが必要である。ラグランジアンが不変に保たれれば、当然運動も不変に保たれる。無論、空間が一様でなければ、座標系の原点のとり方を変化させると、運動方程式が変わってしまうわけである。これは許容されない。

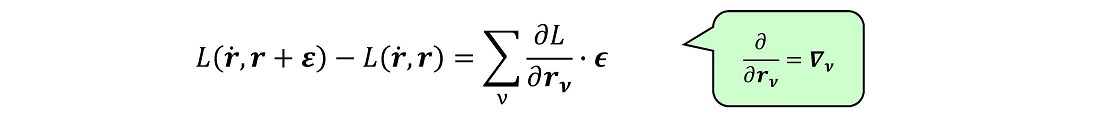
任意の微小量εに対して、ラグランジアンが不変になるためには、次の方程式が成立する必要がある。
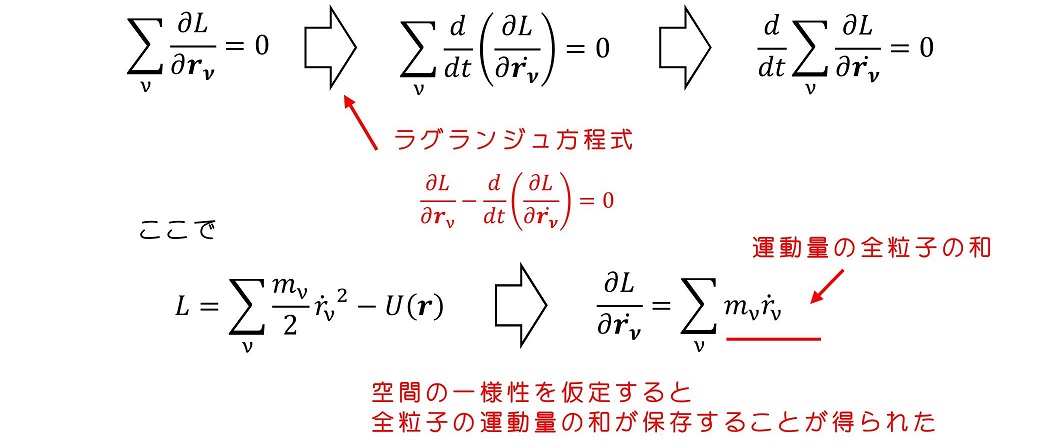
ラグランジアンと角運動量保存則
空間の等方性とはいずれの方向に座標の軸をとっても、運動方程式が不変ということである。すなわち微小に座標の向きを変化させたときに、ラグランジアンが不変であることが必要とされる。