13.1 極座標でのラグランジアン
運動を記述するのに、ラグランジュ方程式を用いることのメリットを挙げておこう。一つに、極座標を用いた運動方程式がかなり簡易に求められることがあげられる。ニュートン方程式で極座標表示を試みるとき、位置ベクトルが変わることによる単位ベクトルerやeθ、eφも時間変化するため、考慮に入れねばならない。一方、ラグランジアンはスカラー量であるため、単位ベクトルの時間変化までいちいち考慮に入れる必要がない。また、ラグランジアンを構成する位置座標qや速度qドットは必ずしもx-y-zの直交座標を選ばなくてもよい。極座標でもよいのである。ラグランジュ方程式はかなり一般性の高い力学運動の記述方法であると知られている。
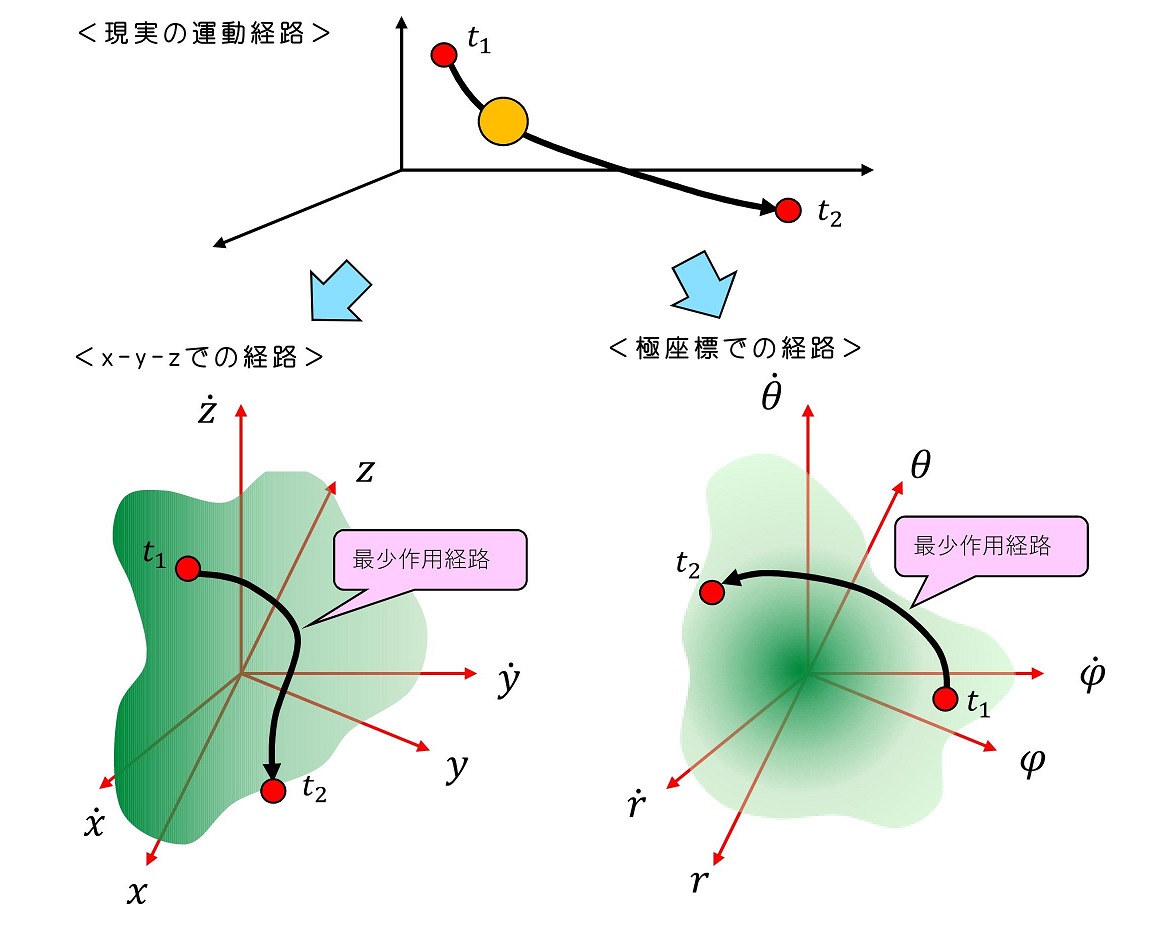
作用が最少になる6次元空間内の経路の「見た目」は、当然座標のとり方で異なるが、現実世界での運動経路は「実質」同じになる。
極座標でのラグランジアンの求め方
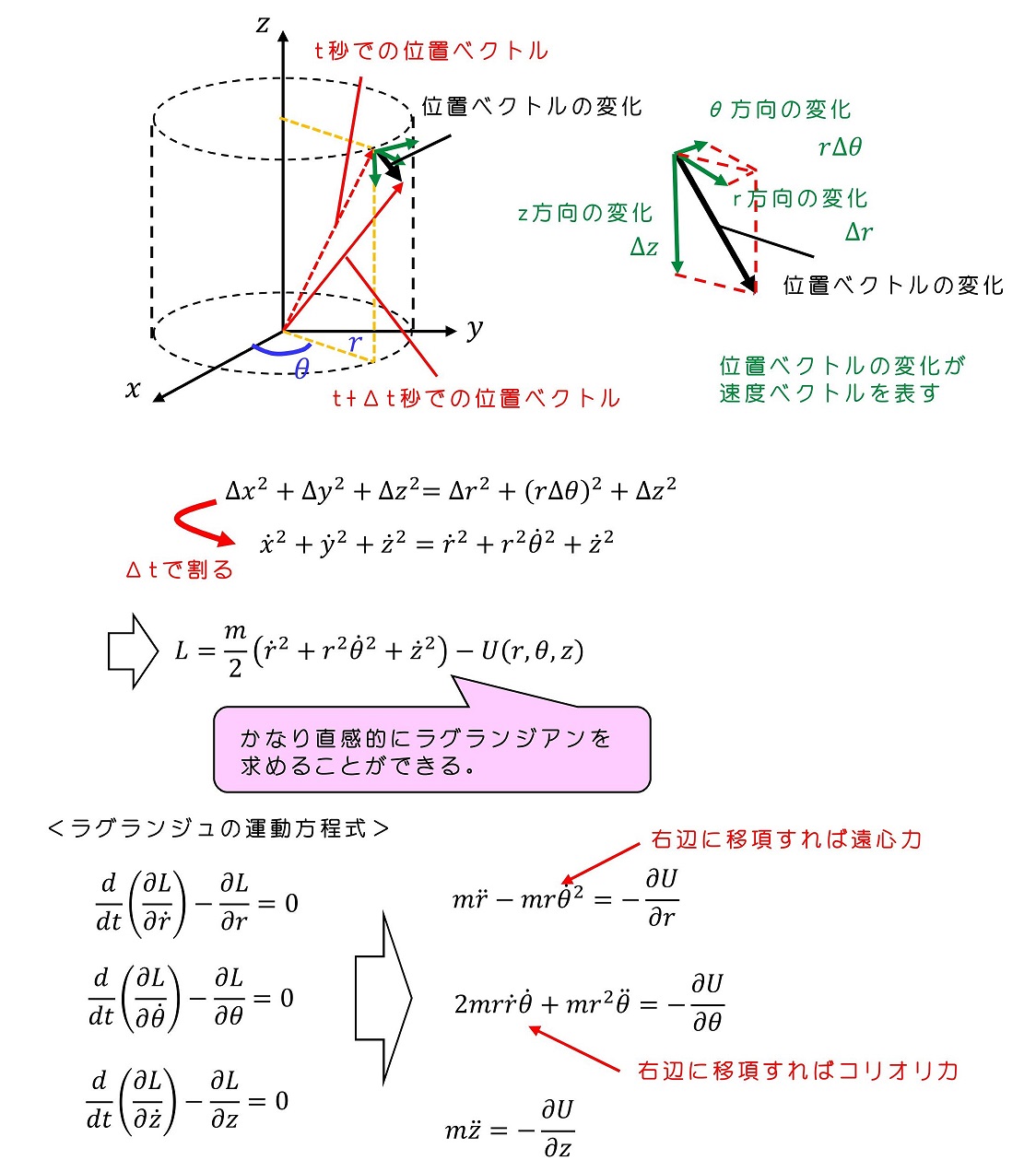
1粒子系の場合を考える。x-y-z系でのラグランジアンは容易に求まる。ここから極座標表示のラグランジアンに書き直す。

<ラグランジュの運動方程式>
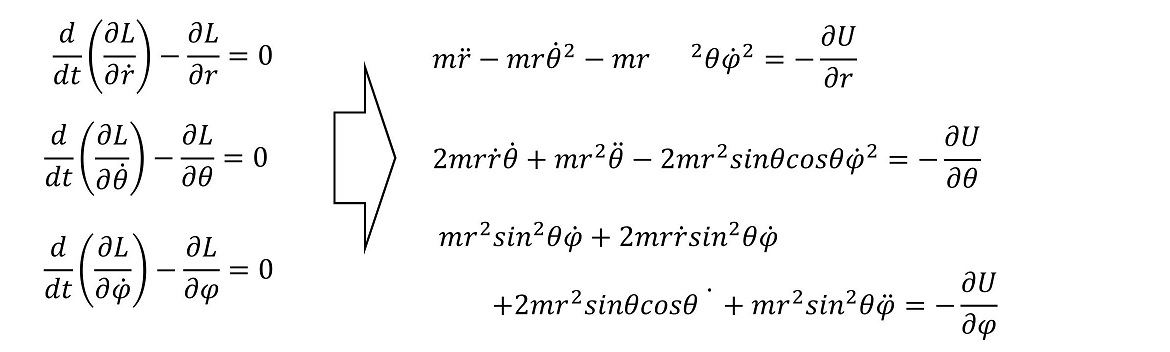
煩雑な運動方程式を、比較的容易に導くことができた。
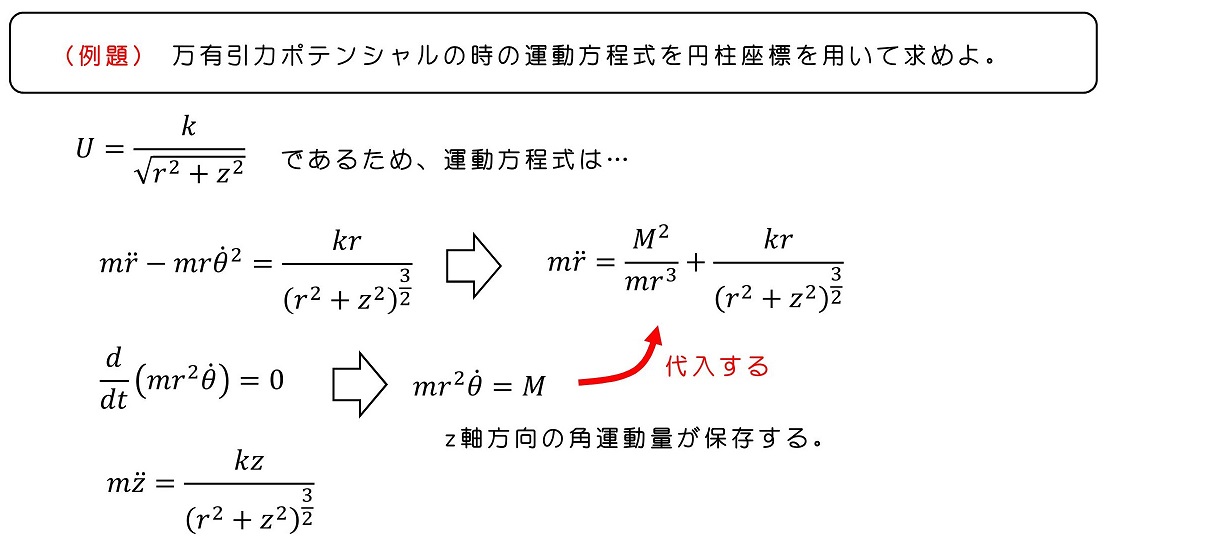
円柱座標でのラグランジアンの求め方
2次元空間の極座標である、円柱座標系も考えてみよう。
13.2 拘束運動にラグランジュ方程式をなぜ適用できるか?
ラグランジュ方程式を拘束運動に適用できるかを考える。運動が拘束されると、運動に利用されるパラメータの数を減らすことができる。これは運動の記述の簡略化につながる。ニュートン方程式では拘束を外力という形で与え、運動を解く必要が出るため、難易度が高いわけだが、ラグランジュ方程式では後述するようにパラメータの減少という形で表れてくるため記述が容易で見通しも立つ。教科書で着目されることは少ないが、パラメータを減らすという作業は、実際には安易に行ってはいけない。力学方程式の適用限界が密接に関連してくる。拘束があるとは、すなわちそこに摩擦が生じ、摩擦は熱力学的な熱エネルギーを生成する。熱は古典力学の適用外である。ばねによる減衰振動のように、摩擦力が速度に比例すると近似的に扱う場合もあるが、多くの場合うまくいかない。力学の適用限界を超えているということである。
もし拘束による摩擦が無視できるほど小さい場合には、安易なパラメータ減らしが許容される。問題文に書かれることは少ないかもしれないが、背後には前提条件として「十分滑らかな拘束」が存在しているわけである。
13.3 2連平面振り子の運動
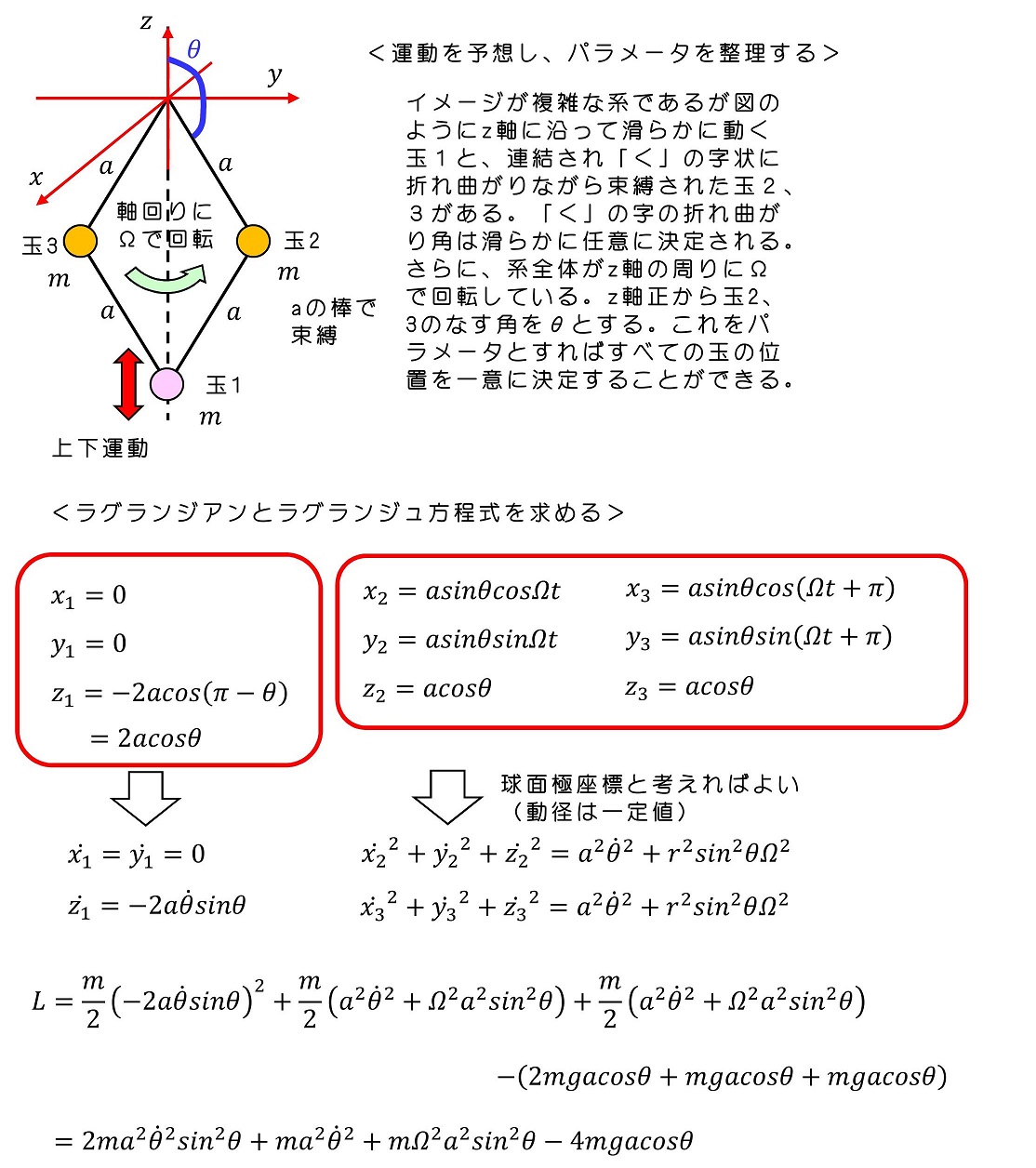
ラグランジュ方程式を用いて、2連振り子の運動を記述しよう。簡略化のために下図のように質量と棒(重さゼロ)の長さが等しいとする。<運動を予想し、パラメータを整理する>

<ラグランジアンとラグランジュ方程式を求める>
位置を振れ角というパラメータを用いて表す。本来3次元×2粒子で位置を表すのに6個のパラメータが必要だが、束縛されているため2個のパラメータで十分である。
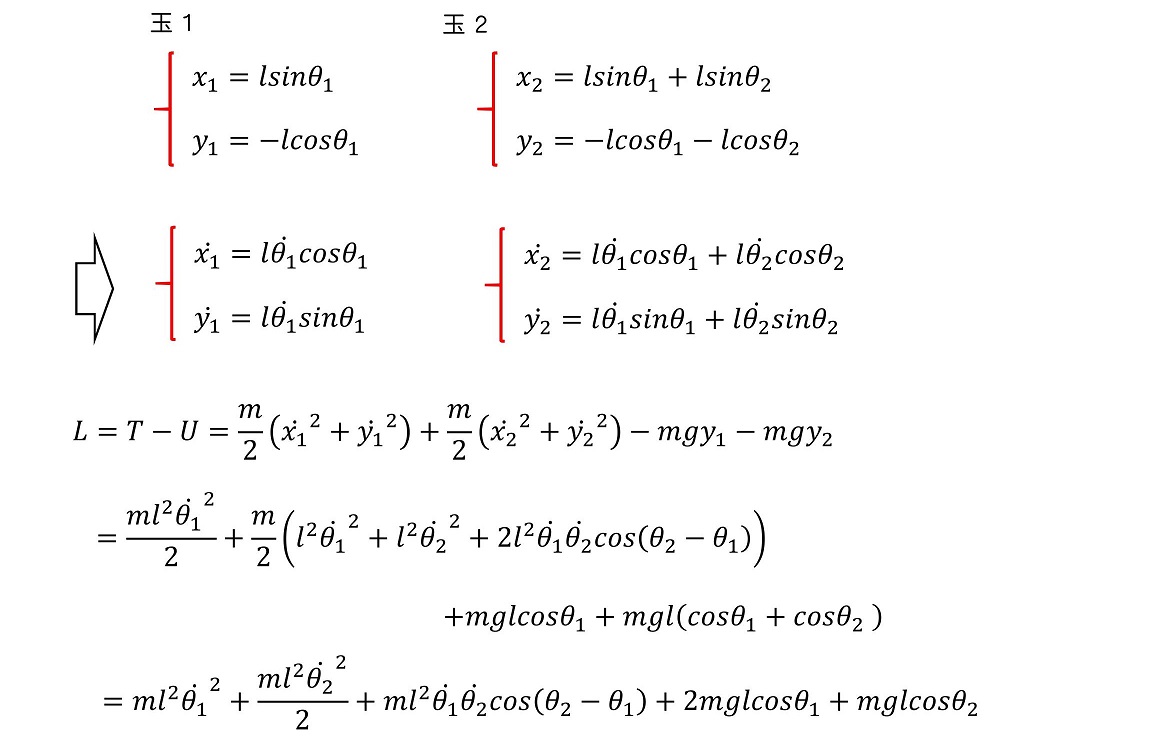

近似をどの次数まで求めるかは、もともとのラグランジュ方程式を見て決める。サインを1次まで求めたとすると、第3項は微小量の3次になる。これが必要な最大次数として十分大きな次数まで求める。

最終的に、運動の見通しをよくするために微小量の3次までは無視するよう近似した。

13.4 ラグランジアンを用いて複雑な束縛問題を解こう①
ラグランジュ方程式を用いると、かなり複雑な束縛問題も容易に求めることができる。その例として次のような問題を考えよう。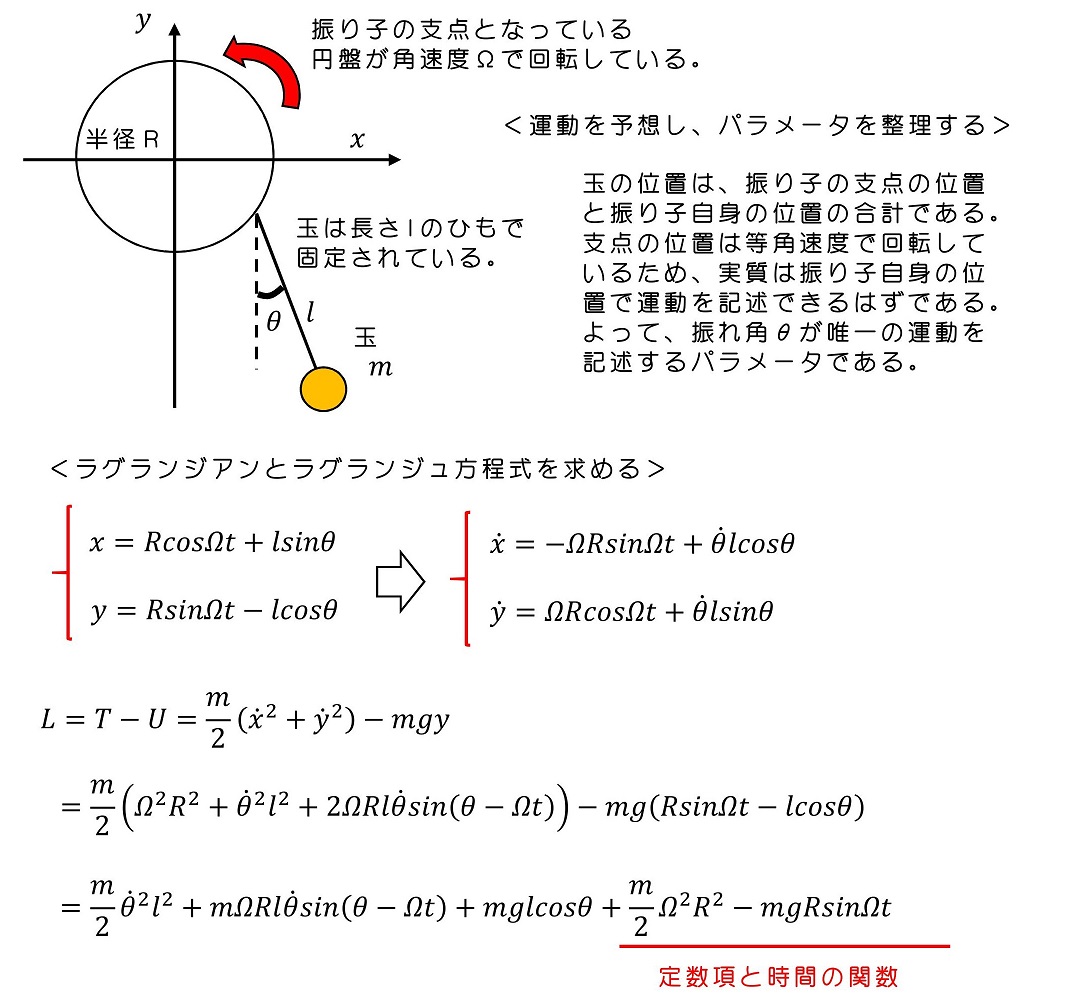
ここで、ラグランジアンの不定性を用いよう。今、定数項や時間のみの関数を削除した新しいラグランジアンL'を用いても、作用最少となる軌跡に変更はなかった。よって、末尾の2項は削除した新しいラグランジアンを用いて議論すれば十分である。
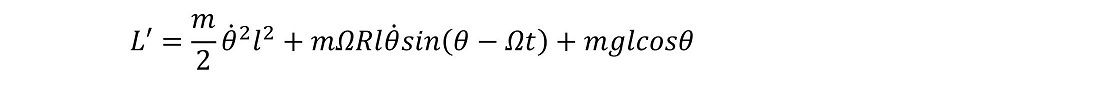

13.4 ラグランジアンを用いて複雑な束縛問題を解こう②
もう一つ、複雑な束縛問題を例題として議論しよう。