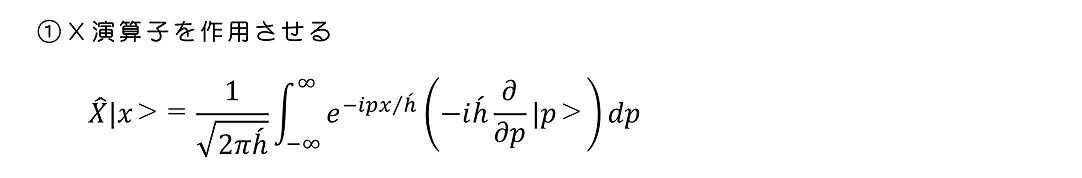2.1 ハイゼンベルグの不確定性原理
量子力学では、状態ベクトルと確率解釈を用いて運動を記述することから始めた。ある瞬間(例えば初期時刻)に位置や運動量は確率的にばらつき、まったく『同じ状態の量子』が100個あったとしても量子の位置や運動量はいろいろな値をとりえた。古典力学からすると驚異的なことである。粒子の初期位置と初期速度(運動量)は当然一意に決まり、その後の運動も一意に決定されるからである。しかし量子力学では、初期の位置や運動量がそもそも一通りに決定されない。この章では、位置や運動量のばらつきに関する法則を扱う。特に重要なハイゼンベルグの不確定性原理から始める。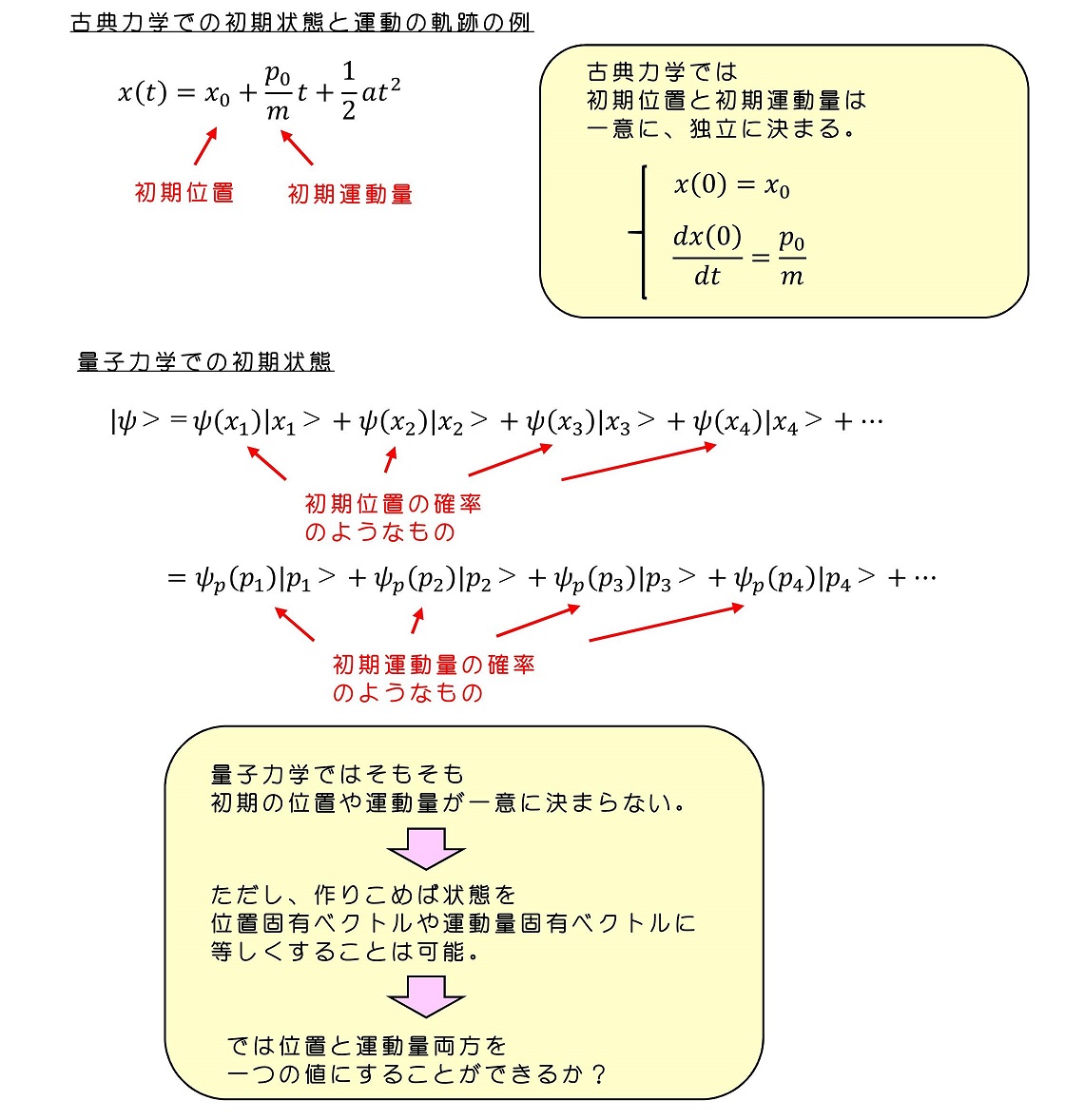
量子力学でも状態を作りこめば、位置の固有ベクトルに等しくすることは可能である。またある運動量の固有ベクトルに等しくすることも可能である。では状態を位置の固有ベクトルと運動量の固有ベクトル、両方に等しくなるよう状態を作りこむことは可能だろうか?
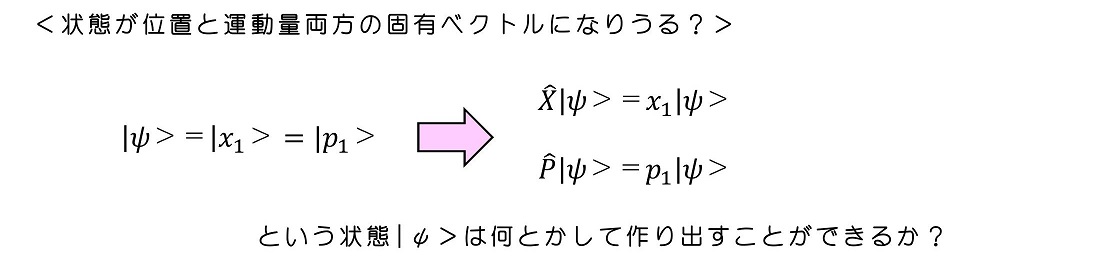
実際に観測してみると、どうやらこのような状態を作り出すことができないらしい。位置を特定できる状態では運動量は決して特定できず、その逆もしかりという結果が出てきた。位置と運動量は両方同時に一つの値に決定できない。驚異的な事実である。原理という位置づけで次のような関係性、ハイゼンベルグの不確定性原理を量子力学では採用することとした。

ΔxやΔpは確率・統計での標準偏差を意味している。状態が位置固有ベクトルに完全に等しい場合は、位置は一つの値しかとることはなく、Δxはゼロになるはずである。同時に状態が運動量固有ベクトルに完全に等しい場合は、運動量も一つの値しかとることはなく、Δpはゼロになる。この場合、Δx・Δpはゼロになる。
しかしハイゼンベルグの不確定性原理はこの状況を否定する。Δxがゼロであった場合、Δpが無限大に発散しなければならない。これなら、Δx・Δpは有限の値になる可能性がある。逆もまたしかりである。
さて、ここでいったん標準偏差を具体的に定義しよう。
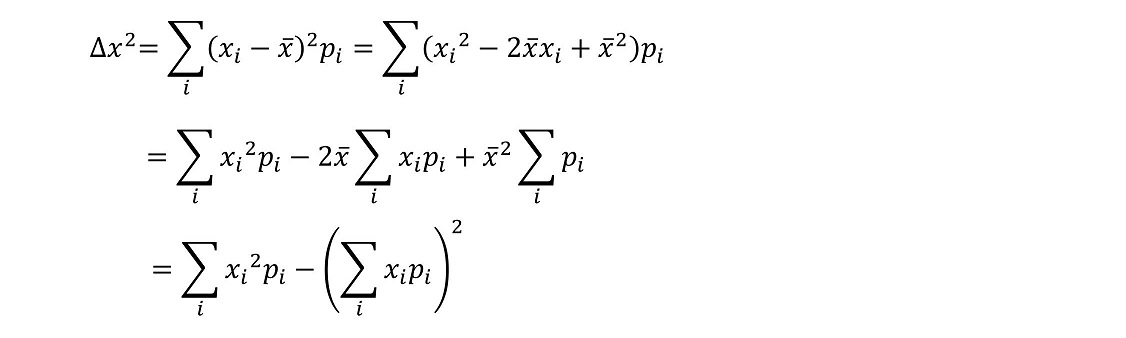
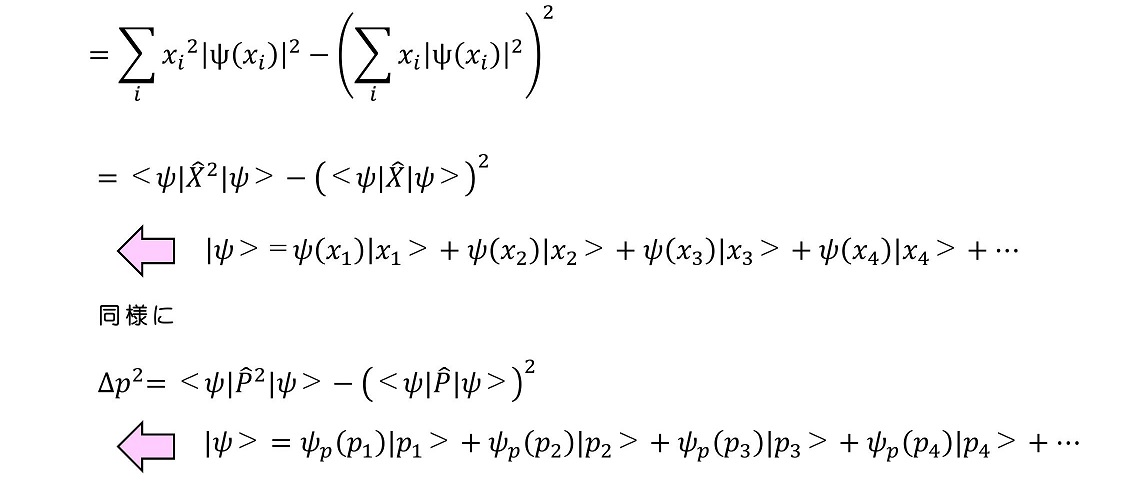
さらに議論を進めよう。ハイゼンベルグの不確定原理は、X演算子とP演算子の「交換演算子」と、密接に関連していることを示す。まずは数学的に成立する次の不等式を紹介しよう。

これを位置と運動量の場合に拡張しよう。左辺はΔx・Δpとなる。右辺はX演算子とP演算子の場合の交換子がわかると計算できる。実は交換子=ihと考えると、量子的な実験結果すべてを説明できることがわかってきた。実際、ihと仮定すれば、ハイゼンベルグの不確定性原理にも矛盾しない。
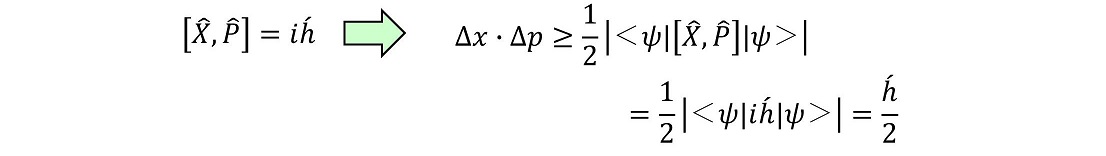
ハイゼンベルグの不確定性原理は、言い換えれば、X演算子とP演算子の交換子がihになるということに等しい。むしろ交換子がihになることのほうが根本的な原理と考えられている。
古典力学で定義された数々の物理量は基本的にX演算子とP演算子を用いることで記述できる。X演算子とP演算子の交換子がわかれば、基本的に任意の物理量同士の交換子を求めることができる。そうすると、任意の物理量同士が不確定性関係にあるか否かも判断できる。
2.2 同時固有状態と縮退について
交換子という概念が出てきたため、もう少し深堀りして、同時固有状態についても考えよう。同時固有状態の例として、位置や運動量の議論を3次元的に厳密化しよう。本来位置演算子はX座標を表す演算子、Y座標を表す演算子、Z座標を表す演算子の3種類が存在するべきで、それぞれの演算子に対応した固有ベクトルと、それぞれの座標値に対応した固有値が存在すべきである。位置演算子同士の交換子がゼロなら、2つの演算子の同時固有状態が存在する。X演算子とY演算子、Y演算子とZ演算子、Z演算子とX演算子は交換子がゼロか?
3次元的な位置演算子

実は、交換子はゼロである。Δx・Δy、Δy・Δz、Δz・Δxもゼロの値をとりうる。Δx・Δyの最小値がゼロにならず有限な値を示す場合、量子のx座標を固定すると、y座標が定まらないことになるわけだが、量子の研究(実験)によると、座標演算子同士に対して不確定性を導入する必要はない。つまり、座標演算子同士の交換子はゼロである。
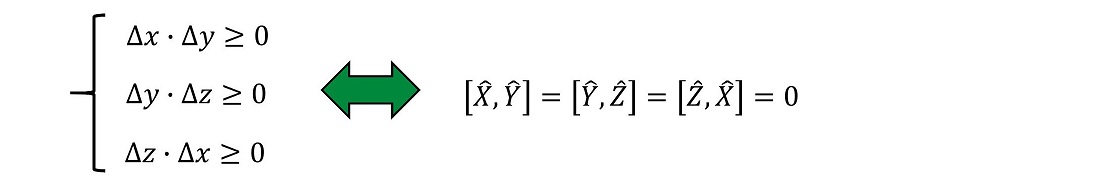
同様に、運動量に対しても3次元的に定義することができる。位置演算子と同じように、運動量演算子同士にも不確定性を持ち込む必要はない。
3次元的な運動量演算子
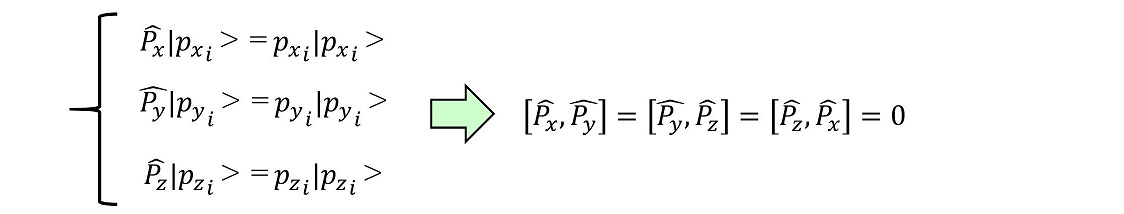
さて、今度は位置座標と運動量の、演算子同士の交換関係を調べよう。これはハイゼンベルグの不確定性原理の3次元化を意味する。
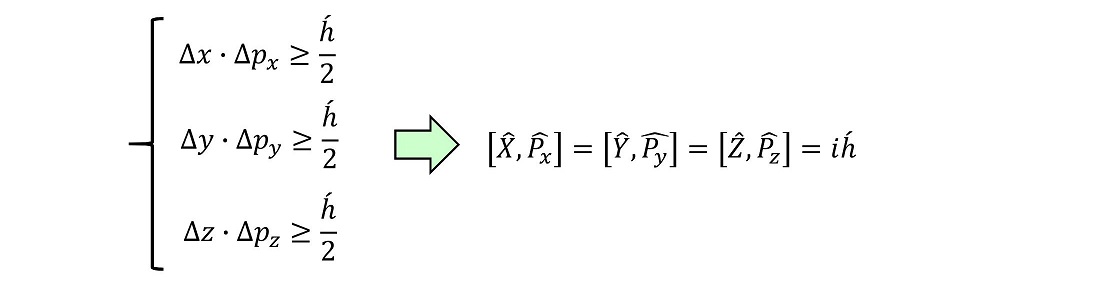
X演算子とPy演算子や、Z演算子とPx演算子との間の交換関係はどのようになるだろうか?これはこれで、逆に奇妙な性質に感じるかもしれないが、直交する関係同士の位置演算子と運動量演算子は交換可能である。
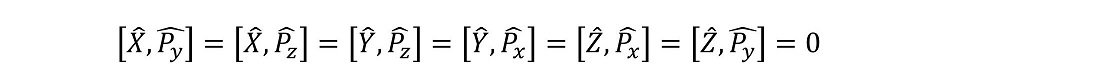
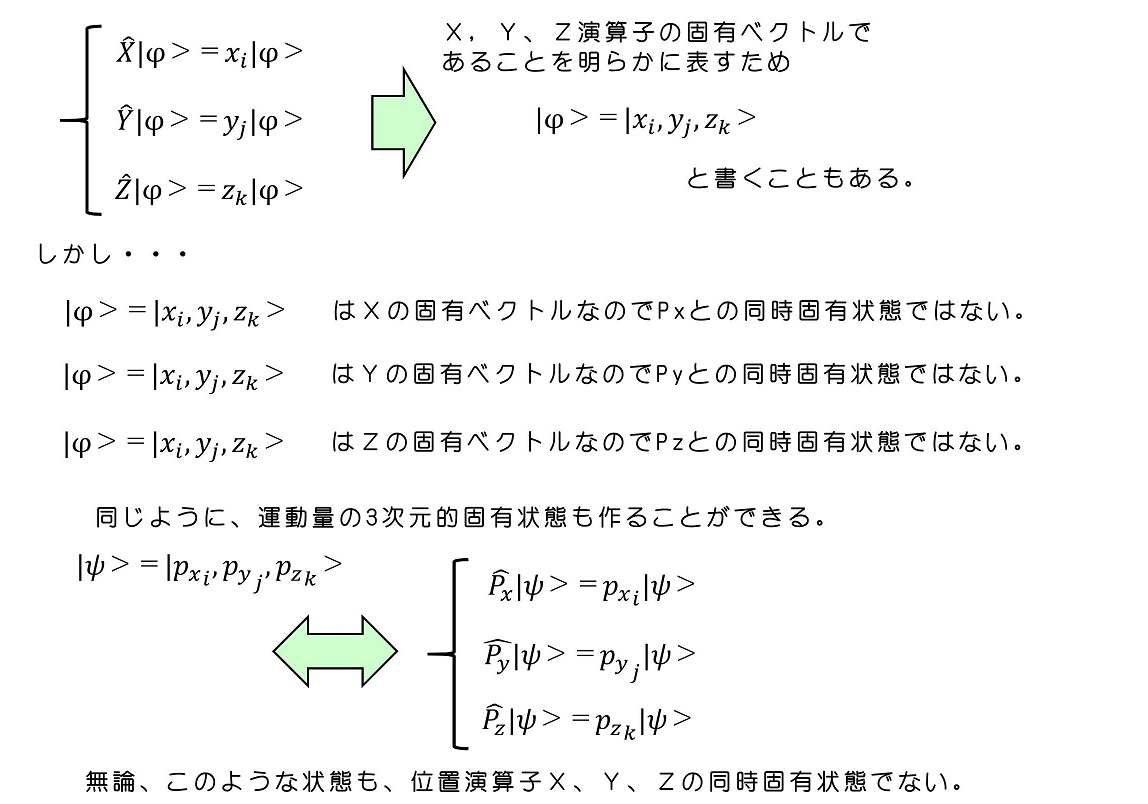
同時固有状態を導入しよう。交換子がゼロの場合、その二つの演算子は同時固有状態を持つという。同時固有状態とは、すなわち次のような特殊な固有ベクトルのことである。

イメージとしては、そのベクトルにX演算子を作用させると、固有値xiを持ち、同じベクトルにY演算子を作用させても固有値yjを持つ。ベクトルは演算子Xと演算子Yの両方の固有ベクトルになる。つまり同時固有状態である。交換子がゼロであることと同時固有状態の関係は次の式でわかる。

位置演算子、運動量演算子の場合を記述しよう。例えば、Xの固有ベクトルが存在したとする。Y演算子やZ演算子と交換可能であるため、Xの固有ベクトルはYやZの同時固有状態にもなりうる。
縮退について
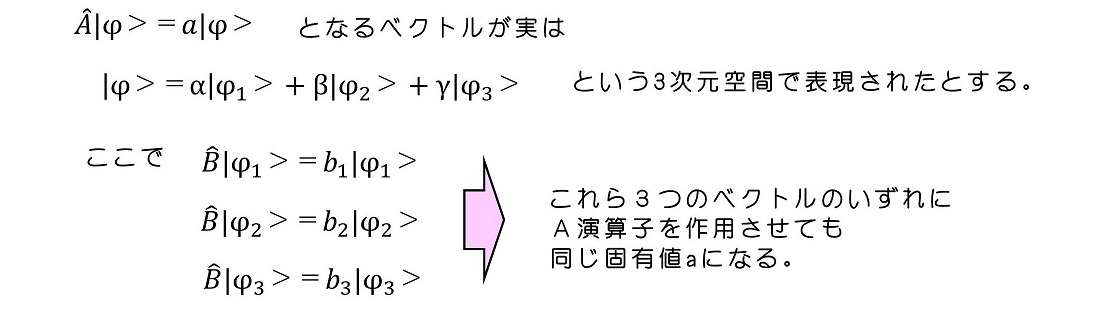
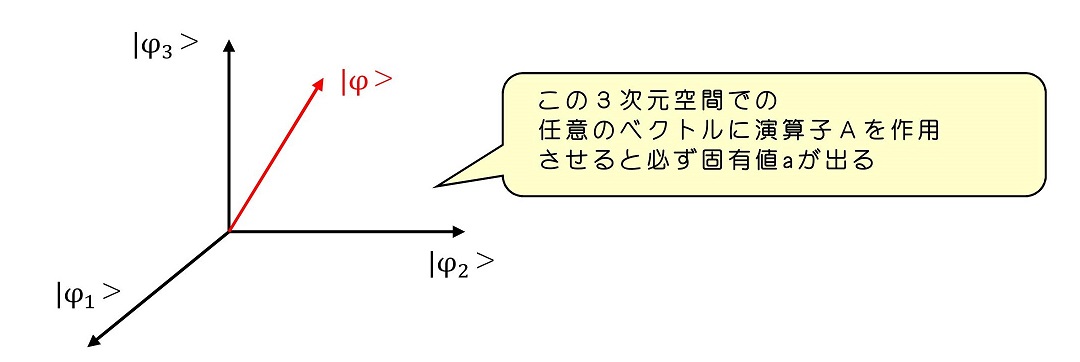
次に、やや早いかもしれないが統一性が出るため縮退という現象についても議論しよう。一般的に、AとBが交換関係にある時、Aの固有ベクトルに対してBの演算子を作用させると、複数の固有値を持ちうる場合がある。これをAがBに関して縮退しているという。
縮退とは、例えばエネルギー的には等しい状態があっても、角運動量が異なっていた場合などに見られる。つまりエネルギーを測定すると、必ず一つの値になっても、角運動量を測定すると、複数の値が観測される状態である。もちろん、エネルギーも角運動量も、一つの値に作りこむことが可能なのは、交換関係より明らかである。
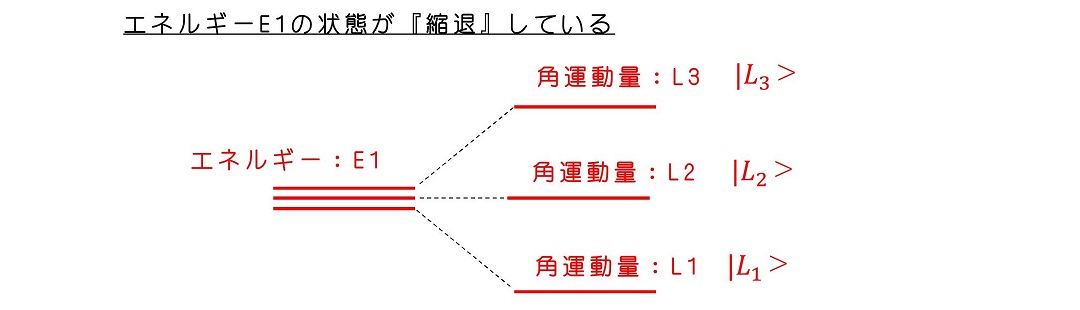
なぜ縮退という考えをあえて議論するのだろうか?このような状態にある量子に外乱、例えば磁場をかけることで、縮退が解けることがある。つまり角運動量が異なると、エネルギー自体も変わる。こうした物理現象を記述するために、縮退という考えが作られた。またのちにフェルミオンというものに分類される量子の分類が出てくる。フェルミオンは1つの状態に1つの量子しか存在しえないという統計性を示す。その際も、縮退していると同じエネルギー状態に複数の状態が入れるようになるため、重要である。

2.3 ユニタリー演算子と平行移動演算子
さて、XとPの関係をさらに深堀りしていこう。X演算子とP演算子は一般にハイゼンベルグの不確定性原理に基づいているのであった。空間の一様性について議論することによって、さらに複雑な事実が導ける。古典力学では空間の一様性と運動量保存の法則が、空間の等方性と角運動量保存の法則が、時間の一様性とエネルギー保存の法則が密接に関連していた。今回の章では保存則までは立ち入らず、まずは状態ベクトルに対して位置座標を平行移動し、新しい原点と座標系で記述しなおす演算子を考えよう。
ユニタリー演算子について(復習)
位置座標を平行移動させたとしても、ベクトルの内積に変化がないとする。物理量やその期待値は内積をとることで意味を成す。座標原点を変えて内積が変わってしまうと、我々の原点のとり方で物理現象が変わってしまうことを意味する。これは明らかにおかしい。
ベクトルの内積値に変化を与えない演算子をユニタリー演算子と呼ぶ。これは状態の時間発展について考えたときに導入した演算子である。
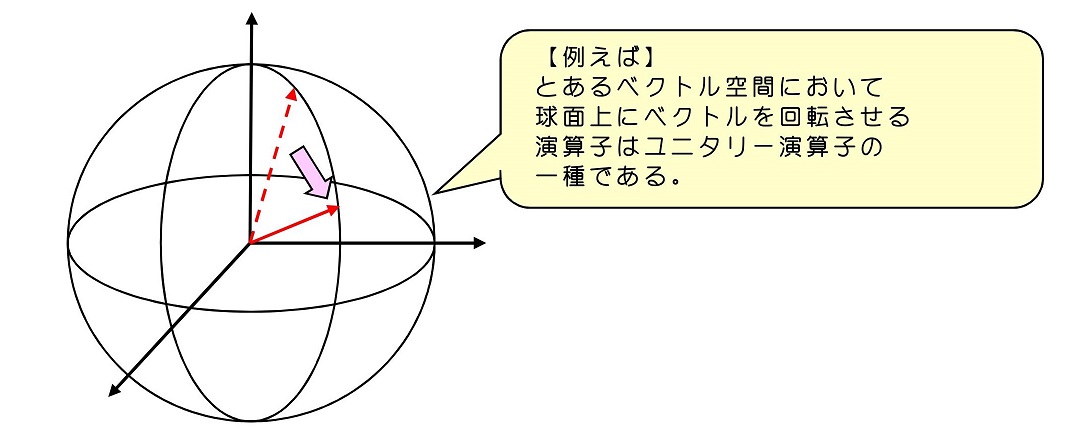
平行移動演算子を導入する
天下り的だが、次のようなユニタリー演算子を導入し、その性質を考えよう。
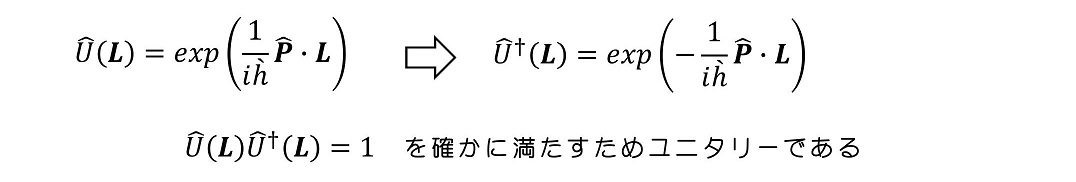
この演算子を状態に作用させた場合の状態ベクトルの空間を考える。

ユニタリー演算子導入後の状態でXの期待値を考えてみよう。どのようになるだろうか?

全く同様にして、次のような事実を導くことができる。

期待値を平行移動させるということは、そもそもの位置の基底のパラメトライズをずらすということと同じ意味である。

2.4 連続的にパラメトライズされた固有ベクトル
今まで、議論をわかりやすくするために本来連続変数であるような物理量も離散的に扱ってきた。例えば、位置演算子の固有値は一般的に連続的であるべきだし、運動量やエネルギーもそうである。もう少し議論を進めるとわかってくるが、境界条件があるような系では、エネルギーなどが離散的になることもある。(このこと自体が古典力学では考えられない驚異的なことだが、それはおいておく)しかし、量子的に物理量が連続的な値をとる場合も非常に多い。離散的な物理量の固有ベクトルで状態を展開する場合と、連続的な物理量の固有ベクトルで状態を展開する場合で、本質的には些細だが、見た目上は決定的な差があるため理解しておくとよい。
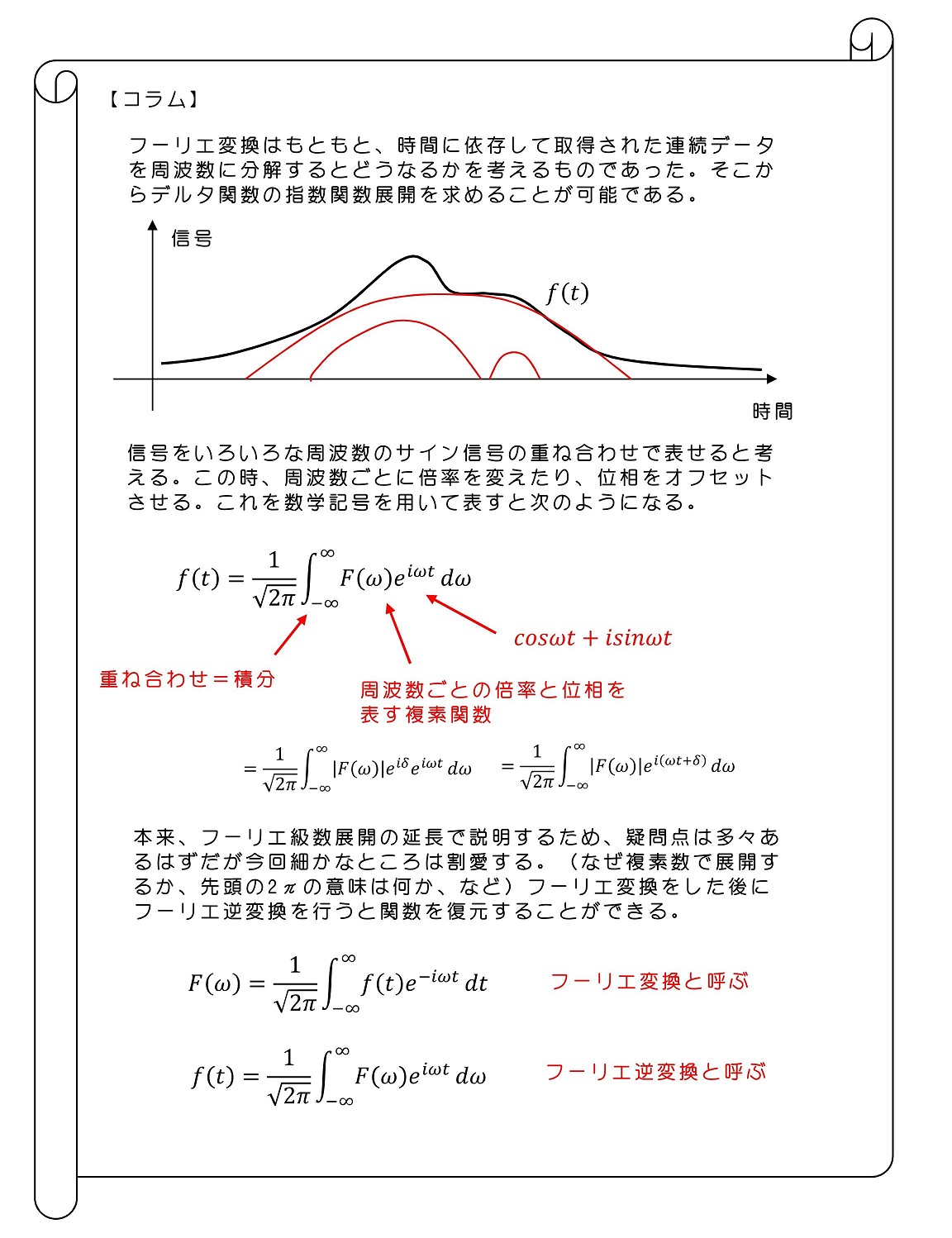
連続変数でパラメトライズされたベクトルを用いて、状態を展開すると次のようになる。
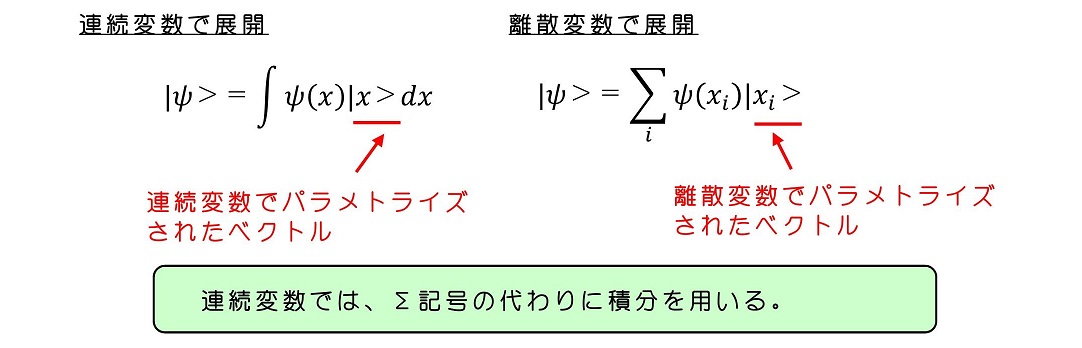
直感的には理解可能である。積分記号は足し合わせと類似に意味を持つ。次に双対ベクトルと内積を考えよう。
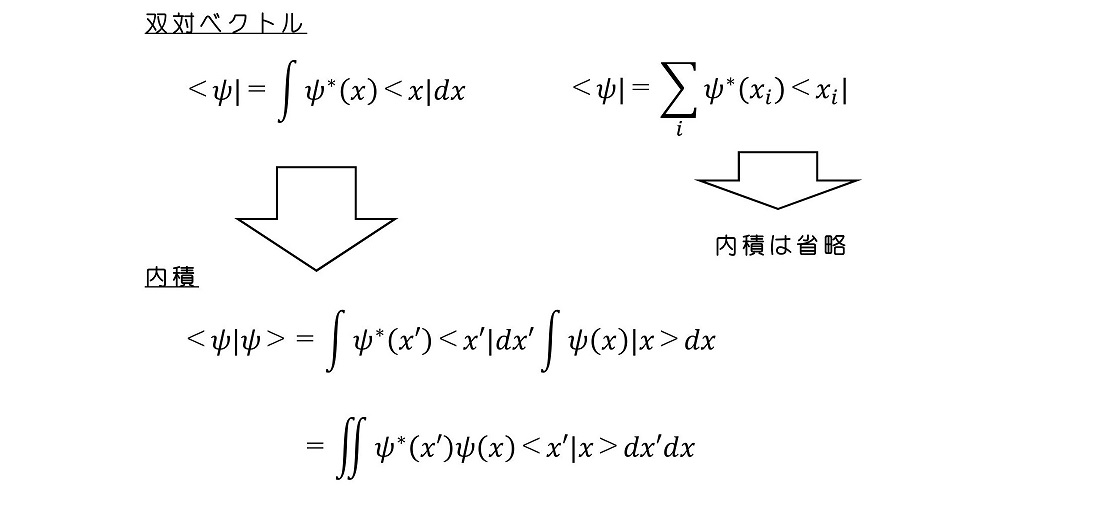
離散変数でパラメトライズされたベクトルで展開した場合、同じ状態同士の内積は確率の合計値になり、その大きさは1になることを前提とした。これを確率解釈と呼んだ。仮に連続変数であった場合も、同じ状態同士の内積は確率の合計値であり、その大きさは1になってほしい。そのために、次のようなディラックのデルタ関数を導入する。
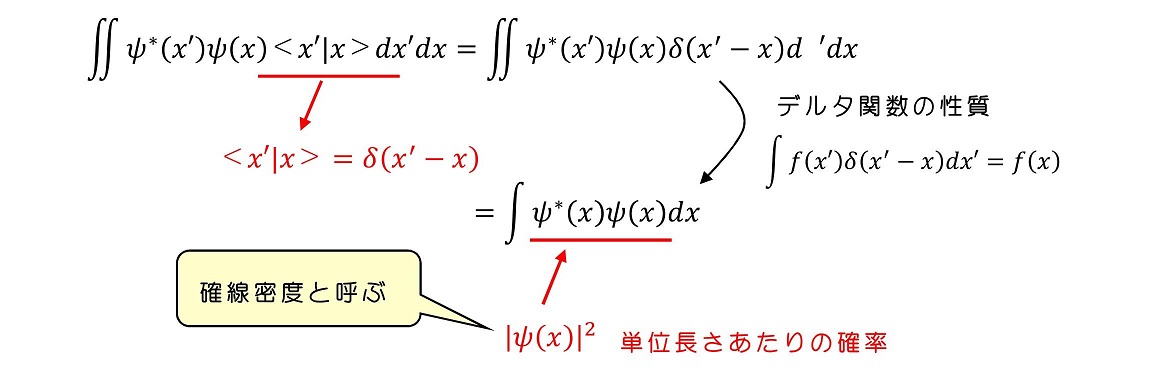
さあ、ここまで議論してきた事実を離散パラメトライズ、連続パラメトライズ比較しながら記述してみよう。

連続変数でパラメトライズされた固有ベクトルの場合、やはり特徴的なのは任意のベクトルを展開するときに積分を用いることと、正規直交性を示すためにデルタ関数を用いることであろう。
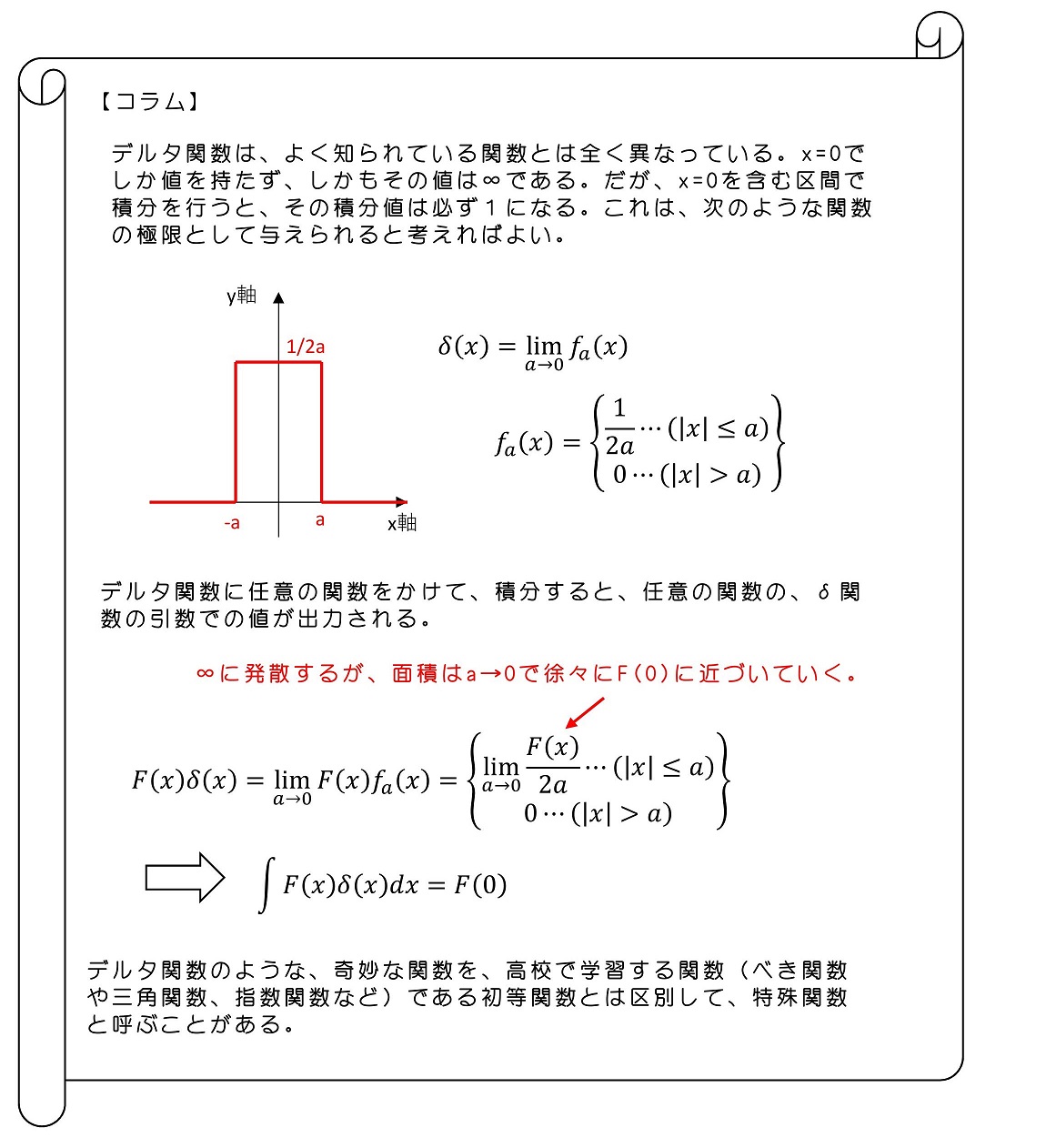
デルタ関数とは、その引数がゼロになるときに無限大に発散し、その他ではゼロになる関数である。ただし、ゼロを含む範囲で積分すると、その大きさは有限である1になる。特殊関数である。
次のような計算を行うことで完全性も示すことができる。

2.5 運動量演算子を位置の固有ベクトルに作用させる
さて、今まで我々は、状態ベクトルを多くの場合位置の固有ベクトルで展開してきた。位置の固有ベクトルに位置演算子を作用させると、その固有値が出てくる。一方、多くの物理量の演算子は位置の演算子と運動量の演算子の組み合わせで構成される。位置の固有ベクトルに運動量の演算子を作用させたとき、どのような性質を示すか考えるのは非常に有意義である。
では、どのように求めればよいか?実は平行移動を表すユニタリー演算子を用いれば比較的簡単に把握ができる。

この事実がわかったことにより、新しい式を導くことができる。
シュレーディンガ方程式を関数方程式にする
シュレーディンガ方程式は、時間発展演算子からベクトル方程式として次のように求めることができた。これを、まずは運動量演算子と位置演算子を用いて書き直そう。
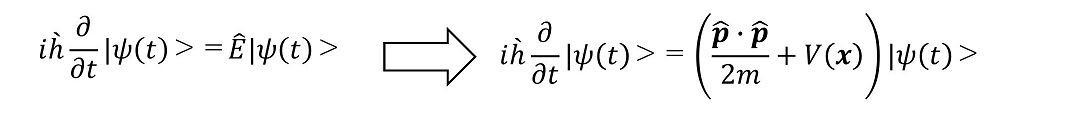
さて、状態ベクトルを位置の固有状態を用いて展開しよう。

シュレーディンガ方程式の関数型は、存在確率がどのように分布しているかを求めるときや、量子が散乱されるときの散乱方向の確率分布を求めるときに、用いると非常に便利である。
運動量の固有状態を位置の固有状態で展開する
おもむろだが、次のように展開できると仮定しよう。この展開は、運動量固有ベクトルが持ついろいろな性質を満足するだろうか?チェックしよう。

P演算子に対して、固有値pを出力し、なおかつ直交性を満たすことが理解された。確かにPの固有ベクトルである。さて、次にX演算子を作用させよう。
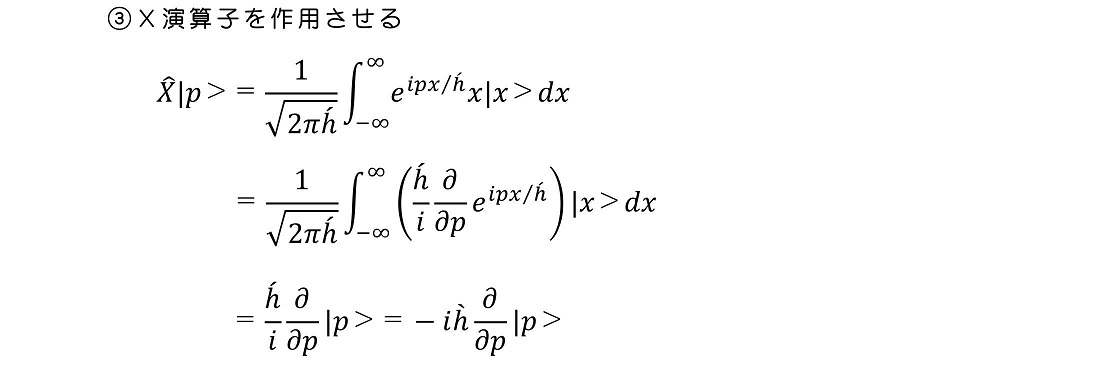
pの固有状態に対して、X演算子を作用させたときの様子もついでに理解することができた。
位置の固有状態は運動量の固有状態で展開できるか?
今、式の対称性に着目すれば位置の固有状態を運動量の固有状態で展開可能するとどうなるか予測可能である。

予測された位置固有状態が、確かに固有値xと直交性を持つかを考察しよう。