1.1 量子力学はなぜ生まれたか?
古典力学は我々の身の周りにある物体の運動を扱う。例えばボールが坂道を転がったり、天井にぶら下がったシャンデリアがわずかに揺れる場合の運動の様子を扱うわけである。この空間にx-y-z座標を自分の好きなようにとり、時間の流れも自分の好きなようにとった時、物体の運動は位置座標が時間とともにどのように推移していくかで記述される。より厳密にいうと、物体の様々な運動をつぶさに観察した場合、力学の第1法則から第3法則までが発見され、それらが空間に一様等方性を、時間に等方性を持たせるような座標、時刻のとり方を保証しているということである。
我々の周りに無限に小さな物体は存在しない。厳密には、観察した物体はすべて有限の物体である。しかし我々は、有限の物体は無限に小さな『質点』の集合だと仮定し、無限に小さな『質点』に働く法則として、力学の第1法則~第3法則を考案したわけである。

しかし、この考察には大いなる仮定を一つはらんでいる。質点の従う運動法則を決めるとき、実際に質点の運動を観察したわけでなく、様々な有限の大きさを持つ物体の運動から、質点という無限に小さな粒子の運動を予測したことにある。
直感的には確かに正しい。太陽も、地球も、岩も、砂の粒も、古典力学に正しく従うことが確認されている。すべての物質は原子とよばれる非常に小さな単位(大きさは10の-10乗メートルほど)で構成されており、原子も原子核という非常に小さな玉の周りを電子というさらに小さな玉が回転しているようなものと知られている。砂の粒よりも小さな原子や原子核、電子が、古典力学に従った運動をしないと考える理由がない。

ニュートン力学が誕生した当初は、測定技術も未熟であり、電子のような非常に小さな運動を観測する手段がなかったが、時代が進むにつれて、電子を観測する手段が得られてきた。電子がニュートンの運動方程式に従うかをチェックする体制が整ってきた。その結果、驚くべきことに、電子のような目に見えないような小さな粒子が、古典力学では全く記述できないということがわかってきたのである。
このようにして、古典力学の限界を知った人類は、非常に小さな粒子を記述するために新たな法則を体系づけ始めた。現在では量子力学は十分に研究しつくされ、100年前では最先端研究分野であったが、今では学部生が授業で習うような理論になったわけである。

アインシュタインの時代に古典理論の限界が、実験でちょうど一斉に指摘され始めた。きわめて鋭い洞察を持ったアインシュタインは、有名な相対性理論はもとより、光電効果、ブラウン運動を始め、極低温比熱やボース粒子の統計性についても定式化し、その後の物理学の基礎になる量子力学、統計力学の発展に貢献した。
1.2 古典力学の限界を示す実験の一例(ダブルスリットと電子銃)
古典力学の限界を示す実験例は多い。いろいろな文献を調べると、光電効果はもとより、プランクの黒体放射や、ド・ブロイ波、ラザフォード散乱などに触れられていることが多々ある。あまりいろいろな実験を紹介すると、量子力学体系の本質がわからなくなってくるため、今回はダブルスリットに電子銃を打ち込むという実験のみを紹介する。まずは、比較のため、次のような野球ボールを使った実験と、波によるヤングの実験ついてみてみよう。

ボールを次から次に投げていく。この時、たまたま1個の粉のついたボールの跡が、スリットありブロックをすり抜けて、後ろの色付きの壁にぶつかることがある。この時、後ろの色付きの壁に1個分の白い粉が付着する。さらに投げ続けると、2個め、3個めのボールが後ろの色付き壁にぶつかり、粉もどんどんついていく。最終的には、ダブルスリットを通りぬける位置は真っ白になり、壁に隠れている部分は元の色のままになるだろう。


一様な正弦波が次から次にやってくることを考えよう。ちょうど波のプールを横から見ているような状態と考えればよい。それが2つスリットが開いている壁にぶつかると、波はそれぞれの位置で回折する。その下流では2つの回折した波が重なり合って、ガラス面に当たる。2つの波の山と山が重なりあうと波が強めあい、より強い山に、谷と谷だと強い谷に、山と谷が重なり合うと山も谷もない状態になる。波は次から次にやってくるため、時間とともにガラス面での山の位置、谷の位置も当然変わってくる。とはいえ、必ず山と山が重なり合う位置では、じき、谷と谷が重なり合う状態になり、再び山と山が重なり合う状態になる。一方、山と谷が重なり合ってキャンセルする位置は、それ以降も永遠にキャンセルされ続ける。それが交互に来る。この結果はヤングの実験でよく知られている。

さて、ここで電子銃によって、電子を打ち出す場合を考える。スリットの後ろには電子が当たるとその箇所が光る板を置いておくとする。どのような実験結果が得られるだろうか?

電子とは何だろうか?イメージとして、電子は原子核の周りをまわっている非常に小さな粒子だと推測される。なぜそのようなイメージを我々は持っているのだろうか?ラザフォード型の原子模型が刷り込まれているから、かもしれない。


仮に、電子が粒だと考えると、ボールをぶつけたときと同じ結果になるはずである。だが、ならない。何本もの縦線状に衝突頻度の高い領域ができる。これは電子を粒として考えると、ありえないことである。壁をすり抜けない限り到達しない場所に、しかも縞状に集まりやすくなるわけである。
電子とは何者であろうか?縞状となって初めて、ヤングの実験を取り扱った理由がわかる。振幅のMAX値が大きいほど白く塗る場合と模様がきわめて似ている。では、電子とは波なのであろうか?答えは否である。波の場合は波面が連続的に見えていた。しかし、今回電子は1粒、1粒スクリーンに衝突している。明らかに波とは異なる。では、電子は粒であろうか?これも答えは否である。2本のスリット上に衝突するわけでなく、何本もの縞状に衝突していくからである。
電子を粒とも波とも異なる、人類がそれまで概念化してこなかった量子という存在として定義しよう。量子とは、確かに粒のような存在なのであるが、その存在する位置座標は確率的で、ある位置での存在確率は波とよく似た性質(回折する、重ね合わせされる…など)を持っていると考えるものである。

1.3 質点と量子との対比、とりうる確率について
もう少し、量子という存在を具体的に、古典力学の質点と比較しながら議論していこう。古典力学では、質点の『状態』を表すために、座標およびその速度や加速度がわかれば十分であった。例えば、『状態』を表す運動量や、角運動量、運動エネルギーや位置エネルギーなど、すべて質点の存在する位置座標やその時間変化から一つの値に決定された。しかし、量子は一つの位置に存在するわけではない。次のように量子の状態を書き表すことにする。
位置が確率的であるということは、その位置座標の時間変化である速度(さらには運動量)もまた、一般に確率的である。今漠然と、『状態』というものを記号『| >』で表した。正直、記号はなんでもよい。量子力学では、なぜかこのようなカギ括弧で状態を表すことが多い。|x1>はx1にいる状態を表す、という風に考えるだけでよい。各位置に存在する状態に、Ψ(x)という重みづけをして、和をとったものを、一般に量子の『状態』、『|Ψ>』で表す。
運動量の状態も同じように、p1にいる状態|p1>やp2にいる状態|p2>の重ね合わせで表すことができる。ここで、|Ψ>は|x1>や|x2>で表すときと、まったく同じものである。ここが量子力学の特殊な部分である。

どのように理解すればよいだろうか?実は、無限大次元のベクトル空間を考えれば、比較的理解しやすい。

状態というものを導入した。状態をいろいろな物理量に対応した基底で展開すると、その係数が確率の「ようなもの」になった。「ようなもの」を外し、確率を明確に導入しよう。

展開した場合の係数の絶対値の2乗を、確率とする。具体的にいうと、x1、x2、x3、x4・・・それぞれにいる状態で展開したときの係数の絶対値の2乗は、それぞれの位置にいる確率であり、同じ状態でもp1、p2、p3、p4・・・の状態で展開したときの係数の絶対値の2乗は、それぞれの運動量の値をとる確率である。
確率をこのように定義すると、ベクトルの内積を用いて、確率に関するいくつかの法則を理解できるようになる。まずは内積について、少し復習しておこう。
1.4 複素ベクトルの内積、エルミート演算子、固有値と固有ベクトル
物理的な内容を把握する前に、数学の体系化をしておこう。まずはベクトルの内積からである。実数ベクトルだけではなく、複素数ベクトルの内積まで含めて考察しよう。
複素ベクトルの内積を作るとき、双対ベクトルの成分が複素共役で定義するのは、ベクトルの大きさを内積によって定義できるからである。

エルミート演算子を定める
次に、エルミート演算子を定義しよう。内積が存在する集合、例えば複素ベクトルの集合を考えたときに、そのベクトルに作用する演算、例えば複素行列を、演算子と呼ぶ。その中でも、特に次のような性質を持つ演算子を、エルミート演算子と呼ぶ。

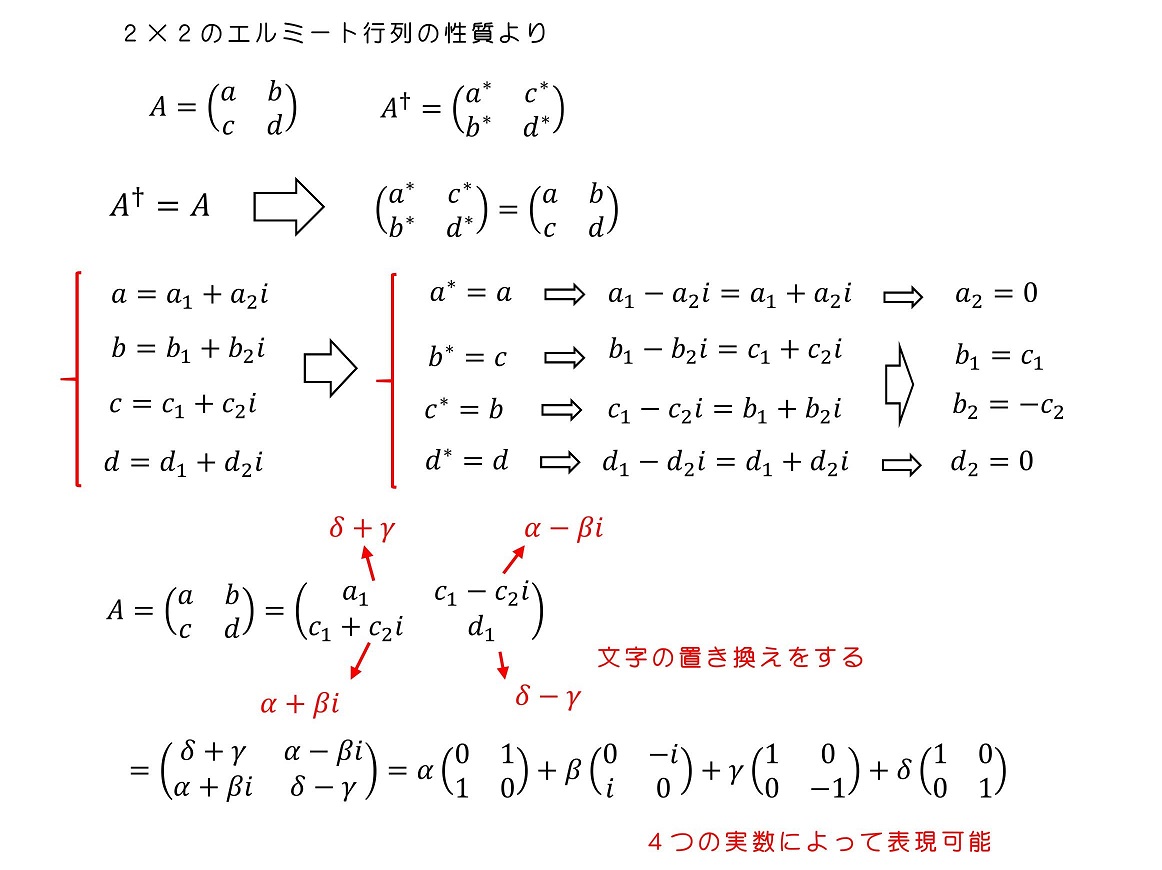
固有値・固有ベクトルとは
演算子、例えばエルミート行列に対して、次のような方程式が成り立つ定数とベクトルが存在する場合、定数を固有値、ベクトルを固有ベクトルと呼び、演算子は固有値と固有ベクトルを持つ、という。

演算子はただ一つだけの固有値と固有ベクトルを持つとは限らない。例えば、n×n行列であれば、最大n個の固有ベクトルを持つことが可能である。

エルミート演算子の固有値・固有ベクトルの性質
エルミート演算子の固有値と固有ベクトルは、いくつかの特殊な性質を持っている。それを示そう。

①エルミート演算子の固有値

②固有ベクトルの直交性

③固有ベクトルので単位演算子をつくる
正規直交基底としてエルミート演算子の固有ベクトルを選び任意のベクトルを表す。

1.5 内積や演算子の考え方を量子の記述に用いる
準備をした内積や演算子の考え方を用いて、量子力学を記述すると、非常にうまくいく。今、固有値に位置座標、固有ベクトルに位置を表す『状態』を持つエルミート演算子Xを導入しよう。
このような位置演算子Xの固有ベクトルを用いて、量子の『状態』を展開してみよう。また、内積を考えてみよう。

内積を計算する

いま、すべての確率を足し合わせると、必ず「1」になるはずである。これを係数ψ(x)が『規格化されている』という。
規格化されているとは、すなわち状態を表す|ψ>ベクトルが大きさ1になるよう|x>の係数ψ(x)が調整されているという意味である。
演算子を作用させ期待値を求める

状態に演算子を作用させ、状態と内積をとると、xをとる期待値になる。この段階で、いったん状況を整理しよう。


さて、ここで疑問を提示しよう。①粒子の状態は、位置座標で一意に表された。それは目視で位置を測定することによって得られた。量子の状態は、どのようにすればわかるだろうか?②またX演算子の形がわかれば、その固有ベクトルも具体的な形で求めることができる。すると状態ベクトルの固有ベクトルで展開した形がわかる。

1.6 量子を状態ベクトルで表すとは?
量子は粒子と異なり、状態ベクトルというかなり特異な量で記述される。しかし、状態ベクトルがあまりに感覚的なせいで、いくつもの疑問点が生じた。状態ベクトルとは何か?観測できるのか?状態ベクトルの存在する空間を作り出すX演算子の固有ベクトルと、それを生み出すX演算子は具体的にどのような形をしているか?順に説明していこう。①量子の状態を表すベクトルは何をどのように観測すればよいか?
粒子の場合は、1粒子を、1回測定することでその状態を表す位置を確定させることができた。量子の場合はどうか?実は、1量子を1回測定するだけでは、その状態ベクトルを導くことができない。

無論、いろいろなシチュエーション下でひたすら観測を繰り返すことによって、状態の係数が満たすべき法則が見えてくる。その法則によって解析的に状態を予想することは可能である。とはいえ、最初はやはり観測を繰り返すしかない。状態ベクトル自体は、X演算子の固有ベクトルが求まれば導ける。

②X演算子の具体的な形と、固有ベクトルの具体的な形とは?
では、X演算子の具体的な形は何になるのだろうか?X演算子が行列のような形で求まれば、そこから固有値と固有ベクトルを求めることは理論上可能である。X演算子はどのような形にすればよいか?実は、X演算子は一意に決まらないことを示すことができる。その結果、固有ベクトルも一組に決まらないことを示すことができる。
X演算子と固有ベクトルの例1

X演算子と固有ベクトルの例2

いずれでも、X演算子を固有ベクトルに作用させると、対応する固有値が導出できることがわかる。ちなみにここで、座標はこの空間に無限の広がりを持っているため、x∞まで存在するとした。今回は、2つの異なるX演算子を導いたが、両者の差に、何か特別な意味はあるのだろうか?

x1に存在する確率ψ(x1)やx2に存在する確率ψ(x2)は量子まわりの環境条件が一緒であれば、ある一通りに決まるはずである。そのため、状態を表すベクトル|ψ>は、上述の例1と例2で異なったベクトルになる。

確かに|ψ>の具体的な形が異なることはわかった。しかし、|ψ>にX演算子を作用させた、双対ベクトルと内積をとったときには、問題なく位置の期待値を求めることができる。実際のところ、我々が測定するのは、この期待値だけであるため、具体的に固有ベクトルが例1の形なのか、例2の形なのかは意味がない。とはいえ、例1のような対角型が一番見やすいため使われやすい。
1.7 オブザーバブル:量子力学での物理量とは
古典力学では、粒子は単一の位置に必ず存在し、粒子の持つ数々の物理量は位置座標およびその時間変化、その組み合わせで求められた。量子力学では、量子は「状態ベクトル」で表され、単一の位置に存在するわけではなく、どの位置に存在するかは確率的であった。さて、古典力学で定義された、位置以外の物理量を量子は持つだろうか?例えば、運動量は?角運動量は?運動エネルギーは?直感的には、位置が一通りに求まらないわけだから、ほかの物理量も一通りに求まらないのが予想される。
位置に限らず、古典力学で定義された我々のよく知る物理量は、すべて対応するエルミート演算子が存在し、すなわち実数の固有値を持ち、正規直交基底をなす固有ベクトルが存在する。これを、その物理量がオブザーバブルであると呼ぶ。

不思議に思うだろう。我々は古典力学の拡張として量子力学を構築しようとしている。量子力学で出てくるのは、すべてオブザーバブルな物理量であり、エルミート演算子のみではないのか?今のところ、まだ難しい議論はしていないが、いずれエルミート以外の演算子が出てくる。その演算子に対応した物理量はオブザーバブルではない。つまり古典力学的に意味がない。
古典力学で知ったいろいろな物理量がオブザーバブルであるということは、それぞれの物理量に対応する固有ベクトルが存在し、正規直交をなしている。つまり、運動量演算子や角運動量演算子、エネルギー演算子が存在し、それぞれに対応した固有ベクトルが存在する。状態ベクトルを今までは位置演算子の固有ベクトルで展開していたが、運動量演算子の固有ベクトル、角運動量演算子の固有ベクトル、エネルギー演算子の固有ベクトルで展開することも許される。ただし、その場合、各固有ベクトルの係数は異なってくる。
位置をx、運動量をp、角運動量をL、エネルギーをEで表す。

さて、一つの状態ベクトルを、別種の固有ベクトルで表すとはどのようなことだろうか?それほど難しくはない。例として3次元に簡素化して考えよう。

もちろん、ある正規直交基底では1つの基底で状態を表されても、別の基底を選択すると、3つの基底が必要になることもある。

1.8 固有ベクトル同士の関係(序章)
X演算子の固有ベクトルで、状態ベクトルを展開していたとする。もしX演算子の固有ベクトルと、P演算子の固有ベクトルの関係性がわかっていれば、状態ベクトルをP演算子の固有ベクトルで展開しなおした場合に焼き直すことができる。
一般に、次のような関係性がわかれば、演算子PとX演算子の固有ベクトルの間の関係性が把握できる。

Pの固有ベクトルとXの固有ベクトルの間の関係性について、演算子の交換関係と密接に結びついているが、詳細は後の章に譲る。
1.9 状態を時間発展させシュレーディンガ方程式を導く
ここまで、状態を様々なオブザーバブルな演算子の固有状態で展開することを考えてきた。しかし、ここで気づいてほしい。古典力学は粒子の位置の時間変化を予測する分野だった。量子力学ではいまだ、量子の状態の時間変化を扱っていない。時間変化を表す演算子を導入することで、所定時間経過後の状態を表すことができる。いままで考えてきた状態を、初期時刻t0の状態と考える

時間発展の演算子は、次のような形になることが知られている。時間発展の演算子は、ユニタリー演算子と呼ばれる演算子の一種である。

ユニタリー演算子とは?
演算子を任意の状態ベクトルに作用させる。演算子を作用させる前のベクトル同士の内積と、作用させた後のベクトル同士の内積が変わらなかったとする。この場合、演算子がユニタリーだという。内積はベクトルの大きさに比例する。演算子がユニタリーとは「ユニット=単位」を変えない演算子という意味である。

内積値が変わらないとは、例えばX固有ベクトルで展開したときの係数の2乗の合計が変わらない、つまり確率の総和が時間によらず「1」であることと一致する。つまり時間発展をユニタリー演算子で表すことは、確率解釈と矛盾しない。先ほど定義した、時間発展の演算子が本当にユニタリーであるかチェックしよう。

確かに時間発展の演算子はユニタリーである
さてここで、初期時刻での状態がわかると、任意の時刻tの状態を予想できるようになった。古典力学では、粒子の位置の時間微分の方程式を基本方程式(ニュートン方程式)として考えていた。量子力学でも状態のの時間微分の満たす方程式を考えたい。どのようになるか?
シュレーディンガー方程式

状態ベクトルの時間変化とは、状態に対してエネルギー演算子を作用させるのと等しいことがわかった。