3.1 量子力学の調和振動子問題を解こう
ここまでの議論で、量子のもついくつかの、重要な性質を記述してきたね。確率解釈、不確定性関係、シュレーディンガ方程式がそれだった。量子力学として、実のところ、まだ具体的な運動については議論していない。ここでは、古典力学でもかなり基本的な運動として紹介した調和振動子(ばねにつながれた粒子)を量子力学に焼き直して、理解してみよう。
どのようにして運動を記述するか?
古典力学では位置の時間変化を求めることで、運動を記述できたと明言していた。量子力学では、状態を位置固有状態や運動量の固有状態で展開し、状態の時間変化を考えることが対応しそうである。しかし量子がパッと目に見えない以上、実はあまり意味がない。仮に運動のある位置に存在する確率がわかったとしても、それをパッと測定することも難しく、理解しにくく、うまみがないからである。古典力学では、確かに粒子の位置がパッとめに見えることを前提にしており、運動の理解を座標に頼るのは有意義ではあるが。
量子を理解する手法として、エネルギーの測定をすることが良い。量子自身のエネルギー変化を電磁波を通して測定することは位置を測定することより容易である。量子を理解する一つの手段として、エネルギーという方法を用いたい。

ではエネルギーの固有状態について考えてみよう。どのようなものになるだろうか?
3.2 調和振動子のエネルギー演算子と自然数演算子
まずはエネルギー演算子を定義しよう。古典力学における調和振動子のエネルギーを位置及び運動量で表し、それらを演算子に置き換えることが必要である。
さて、このエネルギー演算子の固有状態は何かを考えていこう。実はこの解を導こうとする方法として、きわめてエレガントな次のような計算をするとよい。
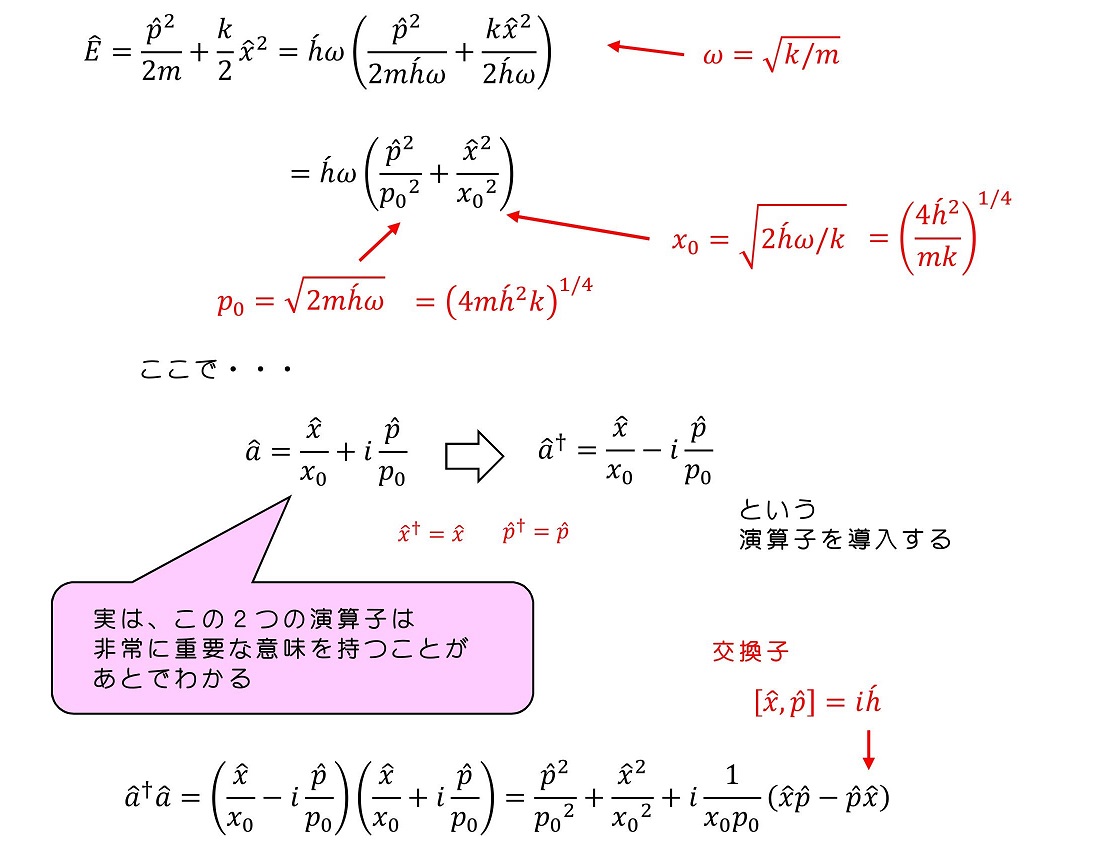
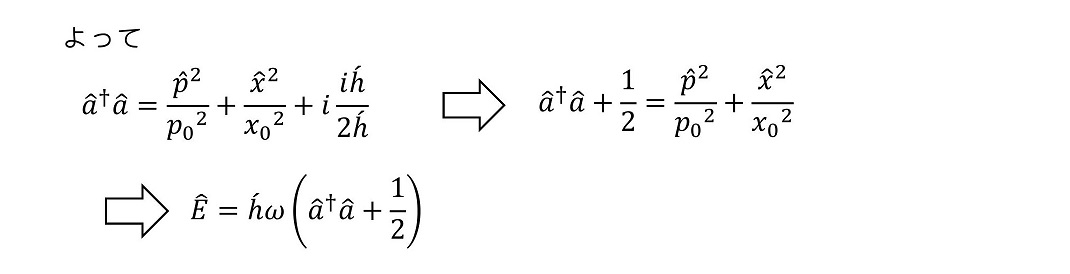
エネルギー演算子を、少し変わった形に書き直すことができた。ここでa演算子を下降演算子、もしくは消滅演算子と呼び、aのエルミート共役であるa†演算子を上昇演算子、もしくは生成演算子と呼ぶ。二つを順に作用させることに相当するa†a演算子は、自然数演算子あるいはナンバー演算子と呼ばれる。
a演算子はエルミート演算子ではない。a†=aとはならないからである。すなわち、a演算子は実数の固有値を持たない、あるいは言い換えるとaはオブザーバブルではなく、a演算子は何かしらの物理量に対応する演算子でもない。その固有状態も、正規直交系をなさない。しかし、N=a†aという演算子は実際のところエルミート演算子であり
一方、N=a†aという演算子は実際のところエルミート演算子である。すなわち実数の固有値を持つ。その固有状態は正規直交系をなす。a演算子やa†演算子をN演算子の固有状態に作用させると、その下降演算子、上昇演算子としての真価を発揮する。


3.3 上昇演算子・下降演算子・自然数演算子の性質
N演算子の固有値と固有ベクトルが必ず存在する。なぜならば、N演算子はエルミートだから。
(i)N演算子の固有値は正である
さて、N演算子を作用させた固有ベクトルと、N演算子の固有ベクトルの内積をとることで、固有値が正であることを示せる。

(ii)a演算子とa†演算子の交換子を計算する
後の考察を簡単にするために、a演算子とa†演算子の交換子を計算してみよう。

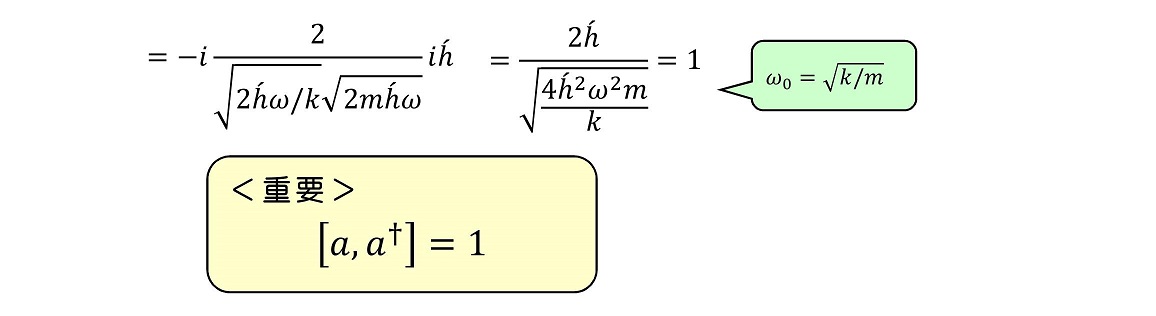
(iii)a演算子をN演算子の固有ベクトルに作用させる
N演算子の固有ベクトルに、a演算子を作用させたベクトルもまた、別の固有値のN演算子の固有ベクトルに比例することがわかる。
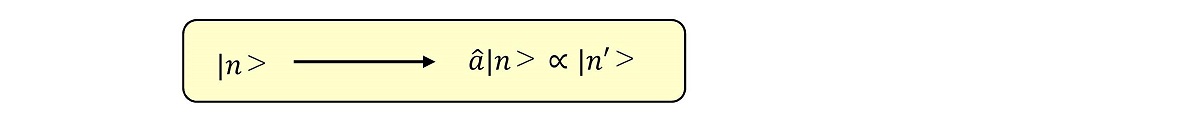
実際に、a演算子を作用させた後の固有ベクトルに対し、N演算子を作用させてみれば、この事実が確認できる。

固有ベクトルは、正規直交をなすように規格化しておくと便利である。今考えているa|n>は規格化された固有ベクトルか調べておくとよい。
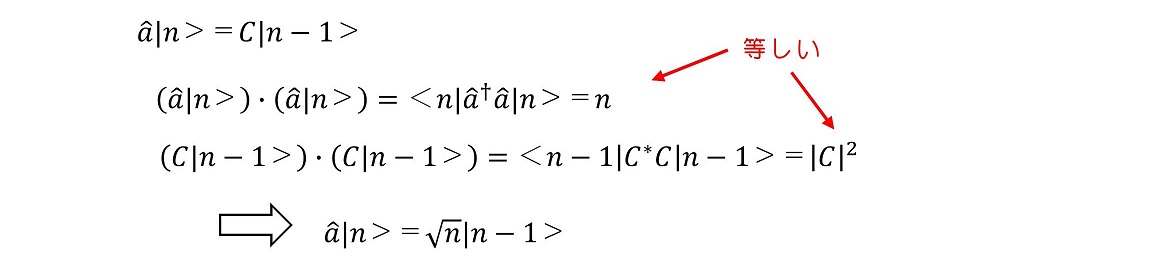
(iv)a†演算子をN演算子の固有ベクトルに作用させる
N演算子の固有ベクトルに、a†演算子を作用させたベクトルもまた、別の固有値のN演算子の固有ベクトルに比例することがわかる。
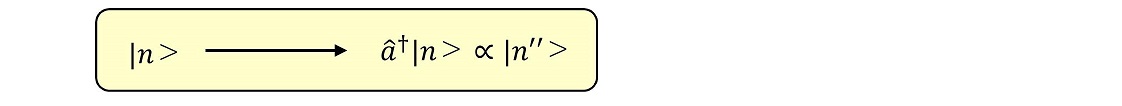
実際に、a†演算子を作用させた後の固有ベクトルに対し、N演算子を作用させてみれば、この事実が確認できる。

固有ベクトルは、正規直交をなすように規格化しておくと便利である。今考えているa†|n>は規格化された固有ベクトルか調べておくとよい。
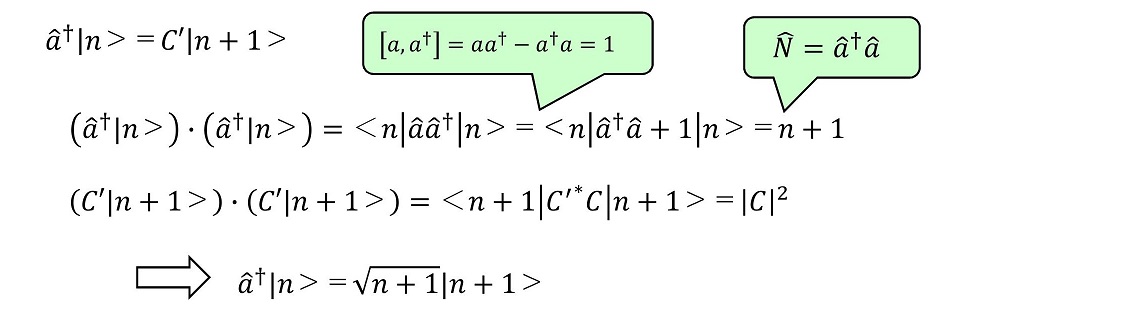
(v)N演算子の固有値が自然数であることを導く
ここまで出てきた(i)~(iv)を用いることで、N演算子が自然数演算子すなわち、固有値として自然数を持つ演算子であることが導き出せる。いったん整理しよう。


n=1.1を固有値に持つ場合、|-0.9>という状態が存在しないと、昇降演算子の理論に矛盾が生じるため、やむなく必要としなければならなかった。そのため、n=1.1が固有値として存在するという仮定に矛盾が生じた。
しかしn=1を固有値に持つ場合、|-1>という状態を用意しなくても昇降演算子の理論に矛盾は生じない。|0>という状態に下降演算子を作用させても係数がゼロになるため|-1>という状態が存在しなくても問題ないからである。

3.4 調和振動子のエネルギー離散性と最低エネルギーについて
自然数演算子を用いてエネルギー演算子を表現することによって、我々は調和振動子のエネルギー離散性や、最低エネルギー順位が有限であることなどの古典力学ではありえないきわめて特殊な結果を導くことができる。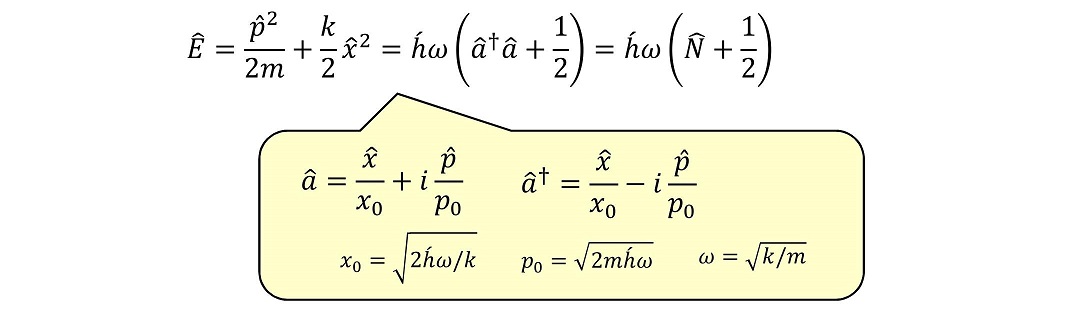
エネルギー演算子と自然数演算子は、交換子がゼロであることより、同時固有状態を持つことがわかる。

さてここで、nがゼロを含む自然数であることを思い出そう。任意の状態をエネルギーの固有状態で展開すると、係数がそのエネルギーをとる確率に対応し、確率に応じて、そのエネルギーの値をとりうる。エネルギー固有値が離散的ということは、その間に当たる中途半端なエネルギーの値を量子がとらないことが示される。
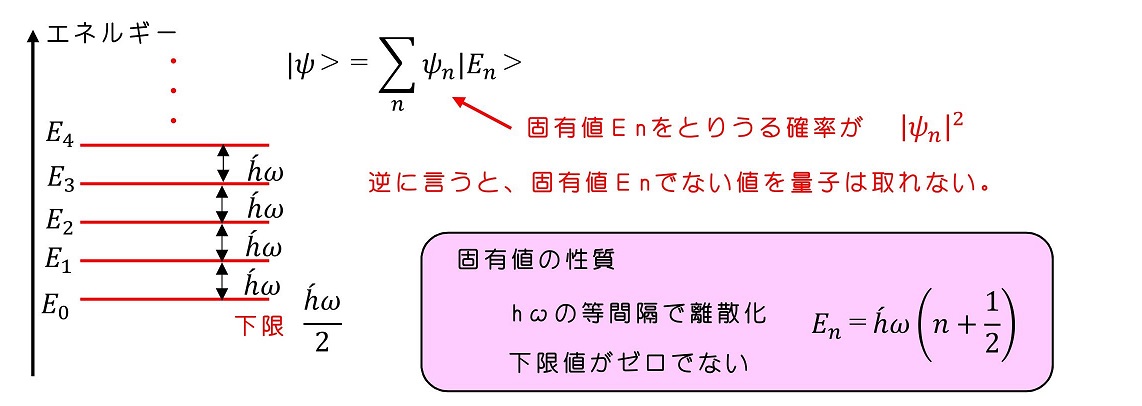
古典力学の理論と比較してみよう。エネルギーの値は、ばねをどこまで縮めて手をはなすかによる。縮める大きさはどのような値でもよく(離散的でない)エネルギーはどのような値でも取りうる。
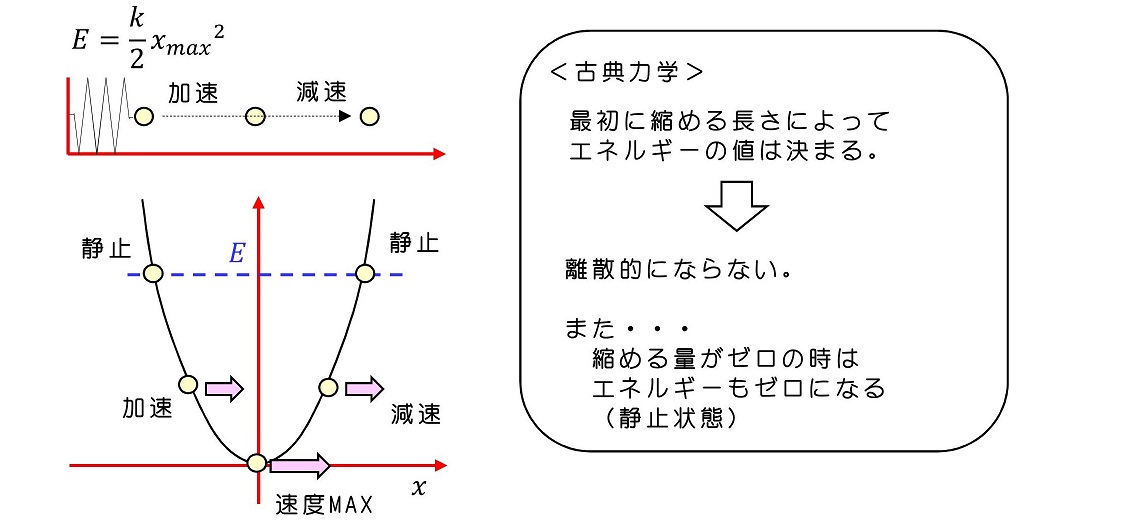
量子力学の場合、最低エネルギーがゼロにならないということは、量子がこのポテンシャル系で古典的に静止しないことを意味している。これはハイゼンベルグの不確定性原理と密接な関連がある。証明しよう。
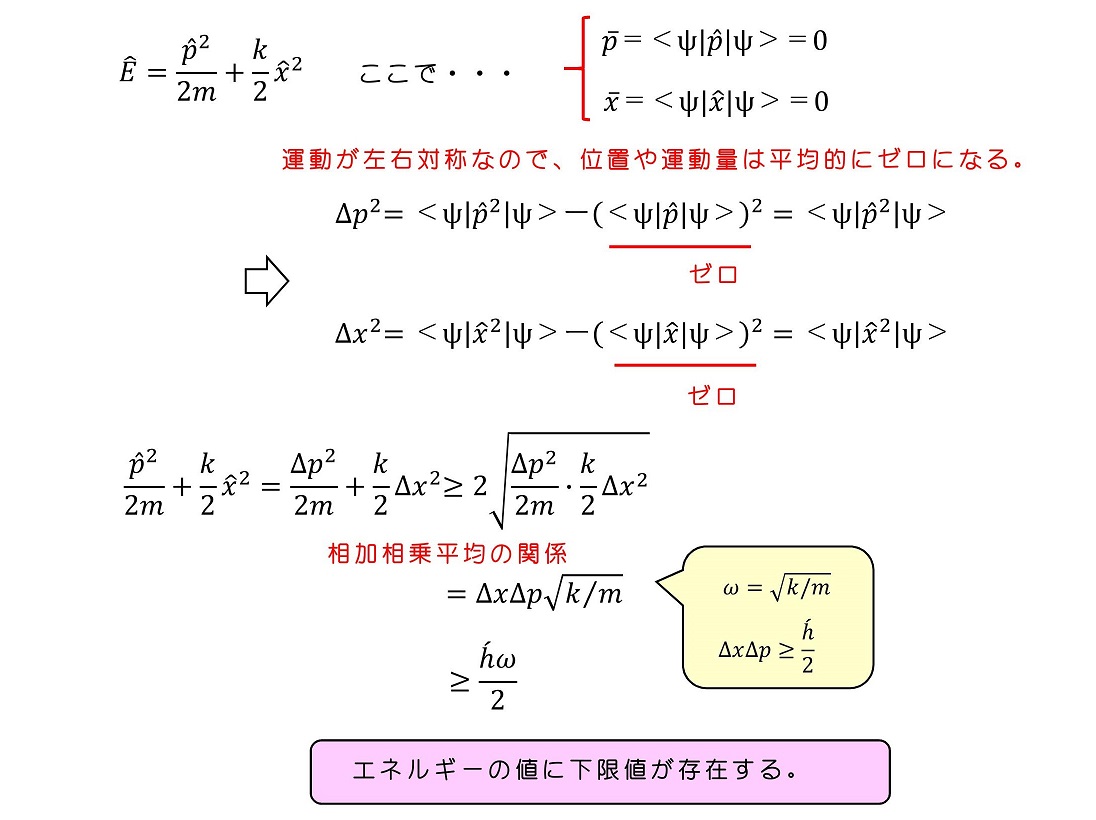
古典力学では、位置と運動量はともに確率的ではなく一意に決定される。すなわち位置や運動量の標準偏差は当然ゼロであり、エネルギーの下限値も当然ゼロになる。しかし、量子的に位置と運動量の標準偏差は同時にゼロにすることができない。ハイゼンベルグの不確定性原理を用いると、エネルギーの下限値が存在することがわかる。
3.5 調和振動子のコヒーレント状態
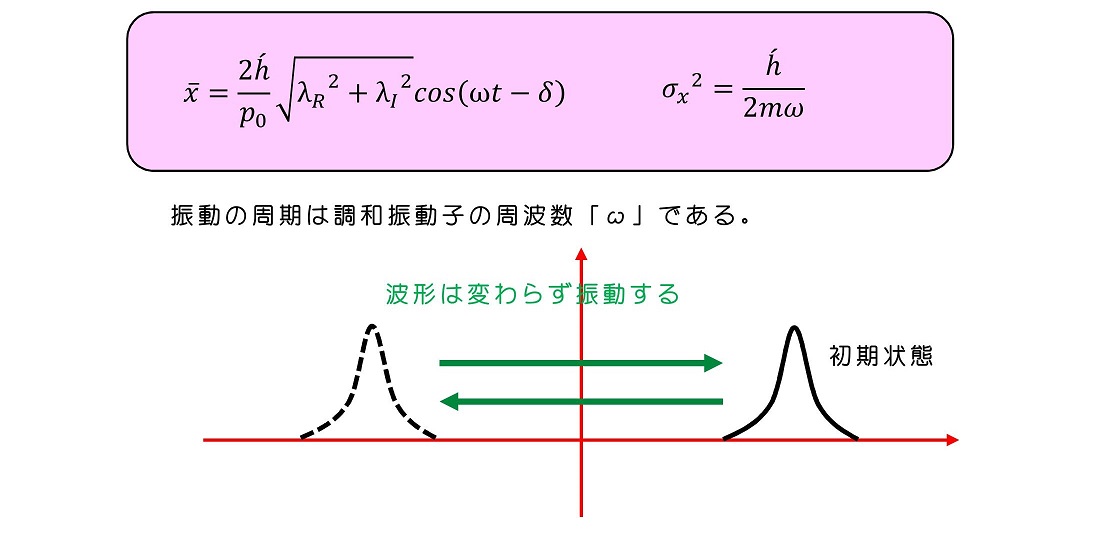
一般にレーザー光のように、波形が時間的に変化しない場合、コヒーレンスが強いという。量子力学で状態は、所定の固有状態で展開され、その係数は確率振幅を意味する。係数すなわち確率振幅の波形が時間とともに変化しない場合、量子状態としてコヒーレンスが強いという。
調和振動子の場合は、下降演算子の固有ベクトルそれ自身が、コヒーレント状態であるため、考えやすい。

では、順を追って|λ>がどのような状態かを検証していこう。
(i)|λ>を|n>を用いて表そう
十分に議論されている|n>を用いてコヒーレント状態を展開してみよう。
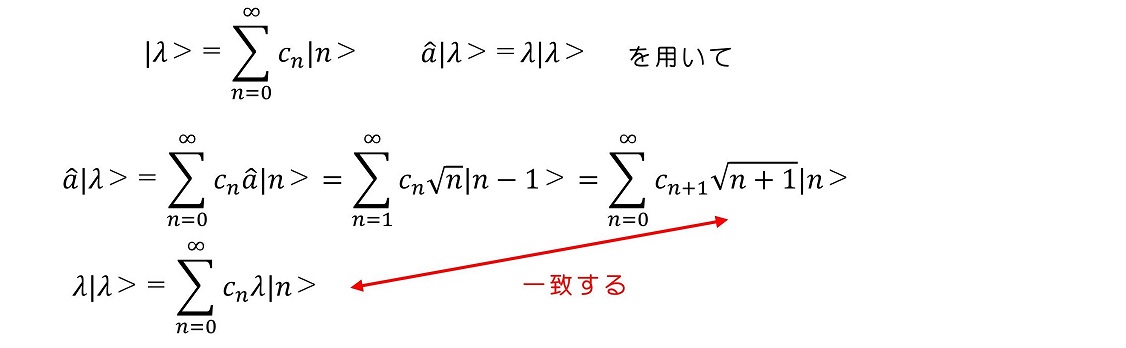
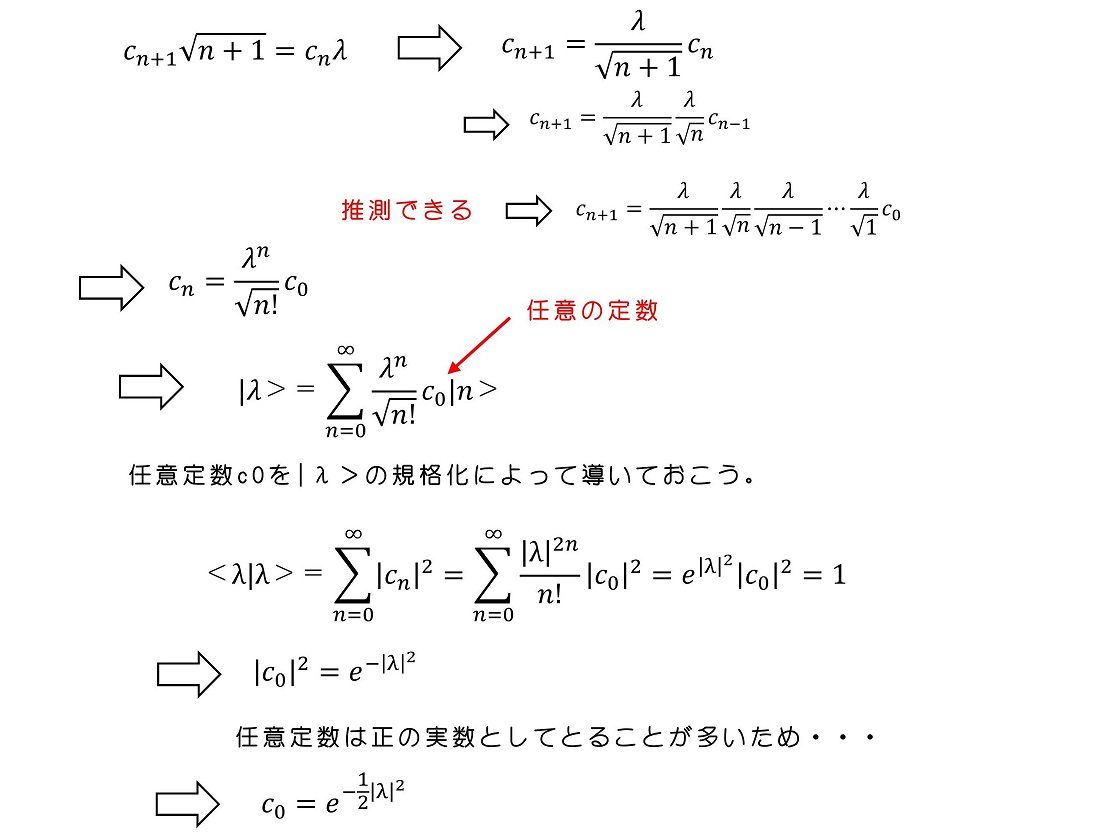
(ii)|λ>を|0>を用いて表そう
一方、|n>は|0>を用いて表すこともできる。
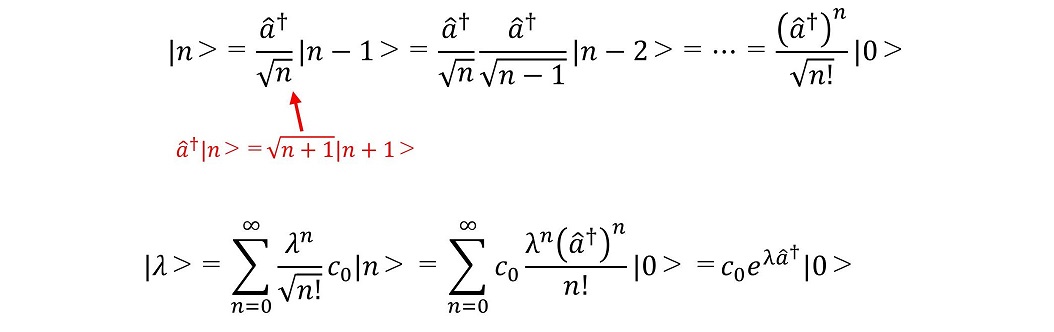
(iii)|λ>を|x>で展開しなおそう
コヒーレントか否かは、位置の固有状態で展開した係数が時間とともにどのように変化するかで決定される。まずはt0での係数を求めよう。


(iv)|0>を|x>で展開する
ψ0(x)=<x|0>だけは、簡単な微分方程式を解くことで解を導きだすことができる。

(v)<x|λ>を関数のみで記述する

コヒーレント状態の確率分布を導くことができた。さて、λは下降演算子の固有値であり、下降演算子はエルミートではないため、一般に複素数である。確率分布をもう少しわかりやすくするために、λの実部と虚部を明らかにして書き直そう。
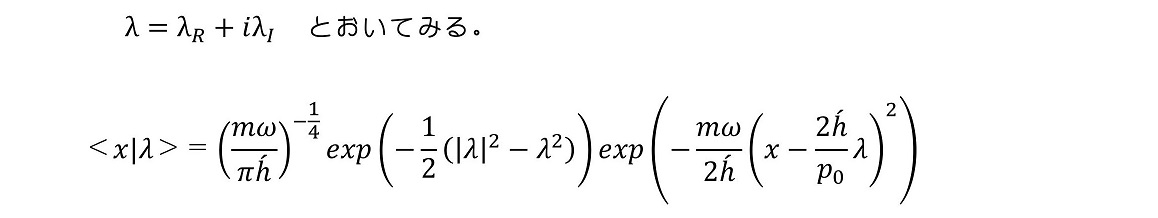

(vi)コヒーレント状態の時間発展を調べよう
確かにコヒーレント状態であることを、時間発展を調べることで調査しよう。時間発展の演算子を作用させればよい。
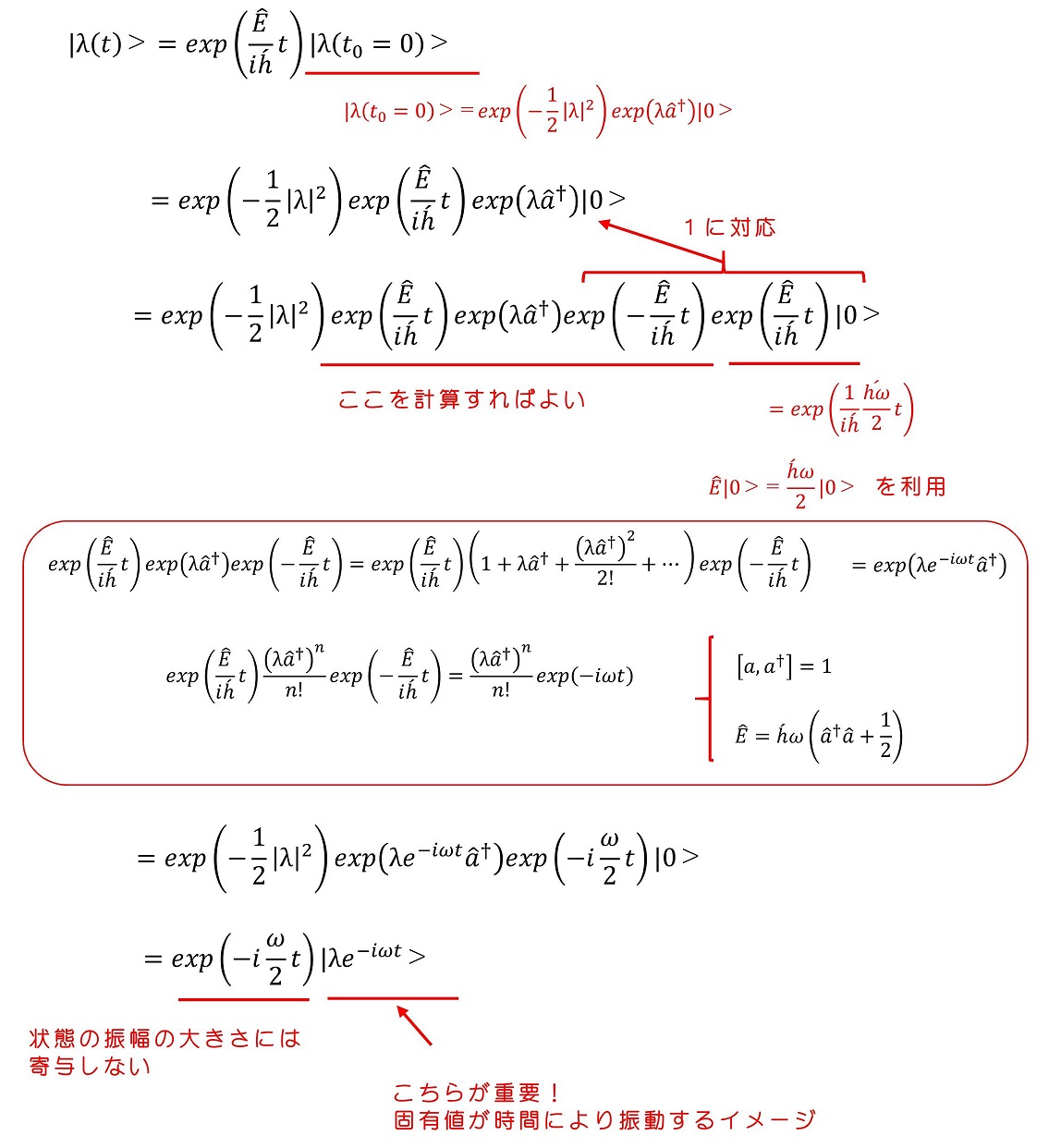
初期時刻でコヒーレント状態がλという複素数で表されたのに対し、t秒経過後ではλexp(-iωt)という複素数で状態が特徴づけられるようになっている。さて、この複素数の実部と虚部を求めてみよう。
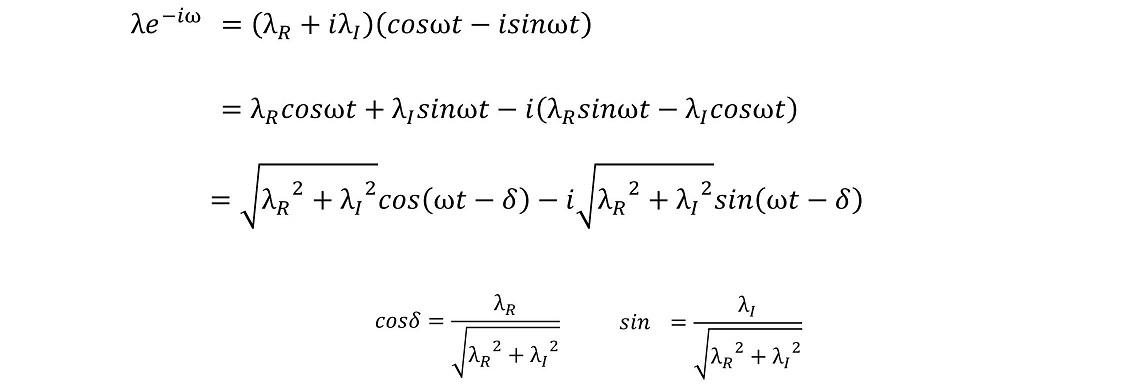
この計算結果を用いて、任意の時刻での位置の平均と分散を計算することができる。